In our daily lives, we're constantly searching for information or trying to find solutions to problems we encounter.
When going through search results on the web, we pick the most relevant articles or resources that we think will help us.
Search is such a part of our lives because we cannot always have the answers. And there are various algorithms that help programs run more efficiently and deal with data more effectively.
What We'll Cover in This Tutorial
- What is a Search Algorithm?
- What is a Binary Search algorithm?
- How Binary Search Works – Divide and Conquer
- Processes involved in Binary Search Algorithms
- Methods Used in Binary Search Algorithms
- Real-life examples of Binary Search
What is a Search Algorithm?
A search algorithm works to retrieve items from any data structure. It compares the data that comes in as input to the information stored in its database and brings out the result. An example is finding your best friend’s number in your contact list of 1,000 numbers.
There are different types of search algorithms. Some of them are:
Linear search algorithms
Linear search algorithms are the simplest of all the search algorithms. As the name implies, they operate in a sequence.
Linear search checks elements in a list one after the other to find a particular key value. This key value is among other items in the list and the algorithm returns the position by going through the check.
Dijkstra's algorithm
Dijkstra's shortest path algorithm is used in more advanced searches. Dijkstra’s algorithm maps out the shortest distance between two nodes. These nodes are often route networks.
This type of search is useful when you're trying to find routes on maps. It gives you options based on finding the shortest path possible.
Binary Search Algorithm
Binary search algorithms are also known as half interval search. They return the position of a target value in a sorted list.
These algorithms use the “divide and conquer” technique to find the value's position.
Binary search algorithms and linear search algorithms are examples of simple search algorithms.
In binary search, the middle element in the list is found before comparing with the key value you are searching for. But in linear search, the elements are taken one by one in the list by looping through and comparing with the key value.

During Binary search, the list is split into two parts to get the middle element: there is the left side, the middle element, and the right side.
The left side contains values smaller than the middle element and the right side contains values that are greater than the middle element. This method uses a sorted list to work.
A sorted list has its items arranged in a particular order. To make search efficient for binary search, the values in the list have to be arranged in the right order to satisfy the process of search. If a list has its values mixed up, it has to be sorted by a sorting algorithm before you perform the search.
Sorting algorithms
Sorting algorithms accept an unsorted list as an input and return a list with the elements arranged in a particular order (mostly ascending order).
There are different types of sorting algorithms, like insertion sort, quick sort, bubble sort, and merge sort.
How Binary Search Works – Divide and Conquer
A binary search algorithm uses a technique called “divide and conquer” to tackle its task. The merge sort algorithm employs the same technique to sort items in a list.
In binary search algorithms, the “divide and conquer” method works this way:
- The algorithm splits the list into two parts: the left side and right side, separated by the middle element
- It creates a variable to store the value of the item to be searched for
- It picks out the middle element and compares it with the item to be searched
- If the items compared are equal, then process ends
- If not, the middle element is either greater or lesser than the item you're searching for. If the middle element is greater, the algorithm splits the list and searches for the element on the left side. If the middle element is smaller, it splits the list and searches for the element on the right side of the list.
You can implement this method using recursion or iteration in the binary search process.
How the Binary Search Algorithm Works – Step by Step
First, before performing the search, you need to sort the list.
Then you create a variable that stores the value to be searched for.
Next, the list is divided into two parts. We sum up the first and last indexes to find the index of the middle element in the list.
When the calculated value of the middle element index is a float (like 3.45), we take the whole part as the index.
Then we compare the value we're searching for and the middle element.

Binary Search Use Case
Condition 1
If the middle element is equal to the value to be searched, the position where the value is will be returned and the process is terminated.
if middle element == to_search
return position of middle element
*code ends*
Using the Image above as an example:
The middle element = 23, the target value/to_search = 23. Comparing the two values, we see that they are equal on both sides. 23 appears at index 2 in the list. That is the output of the code and the process ends.
Condition 2
If the middle element is not equal to "to_search", then we check the following scenarios:
Scenario 1: if the middle element is greater than the value to be searched:
if middle element > to_search
- the search moves to the left side because the values are less than the middle element
- the position of the middle element shifts to the left by 1
- new_position = index(middle element) - 1
- a new search begins and the search ends at that new position and it takes all the values before it.
Using the image above as an example:
middle element = 23
to_search = 4
if 23 > 4
- we move to the left side because all numbers less than 23 are stored there. index (23) = 2
- new_position = index(23) - 1 = 2-1 = 1
- The search will end at index 1 and take all other value(s) before index 1
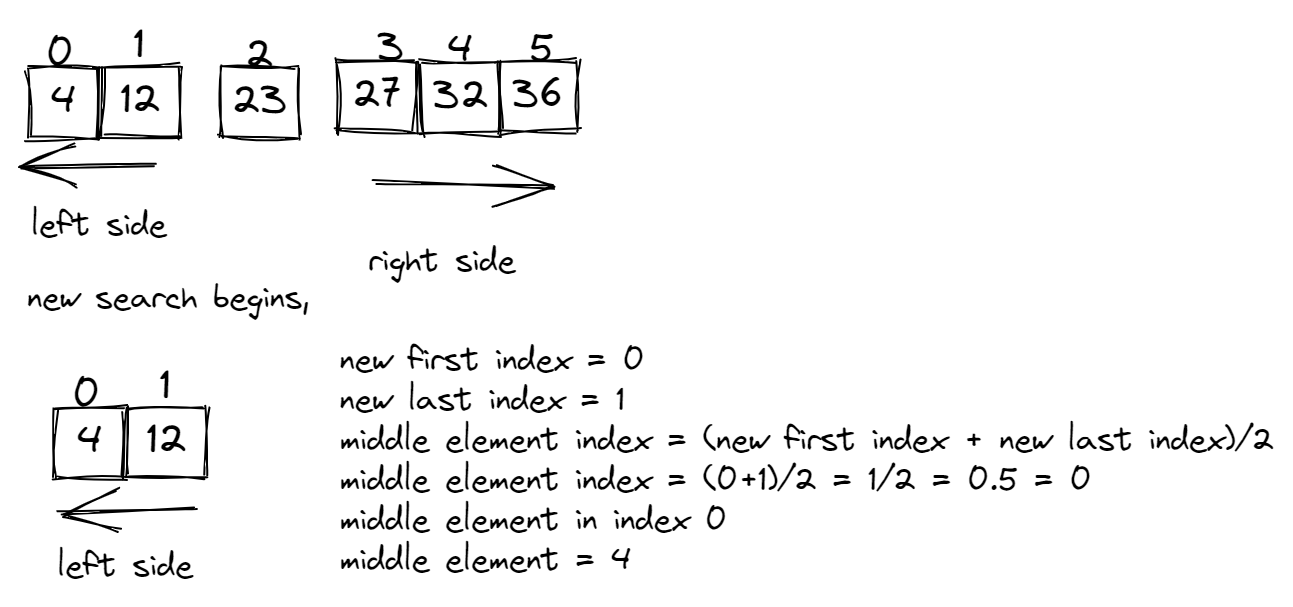
Comparing the new middle element (4) to the target value (4), we see they are equal. So the search is terminated and the output is the position "4" occupies in the list (which is index 0).
Scenario 2: if the middle element is less than the value to be searched:
if middle element < to_search
- the search moves to the right side because the values are greater than the middle element
- the position of the middle element shifts to the right by 1
- new_position = index(middle element) + 1
- a new search begins at the new position and ends at the last index in the list
- all values are taken from the new position to the end of the list
Using the first Image as an example:
middle element = 23
to_search = 32
if 23 > 32
- we move to the right side because all numbers greater than 23 are stored there. index(23) = 2 ,
- new_position = index(23) + 1 = 2+1 = 3
- The search will begin at index 3 and take all other value(s) after index 3
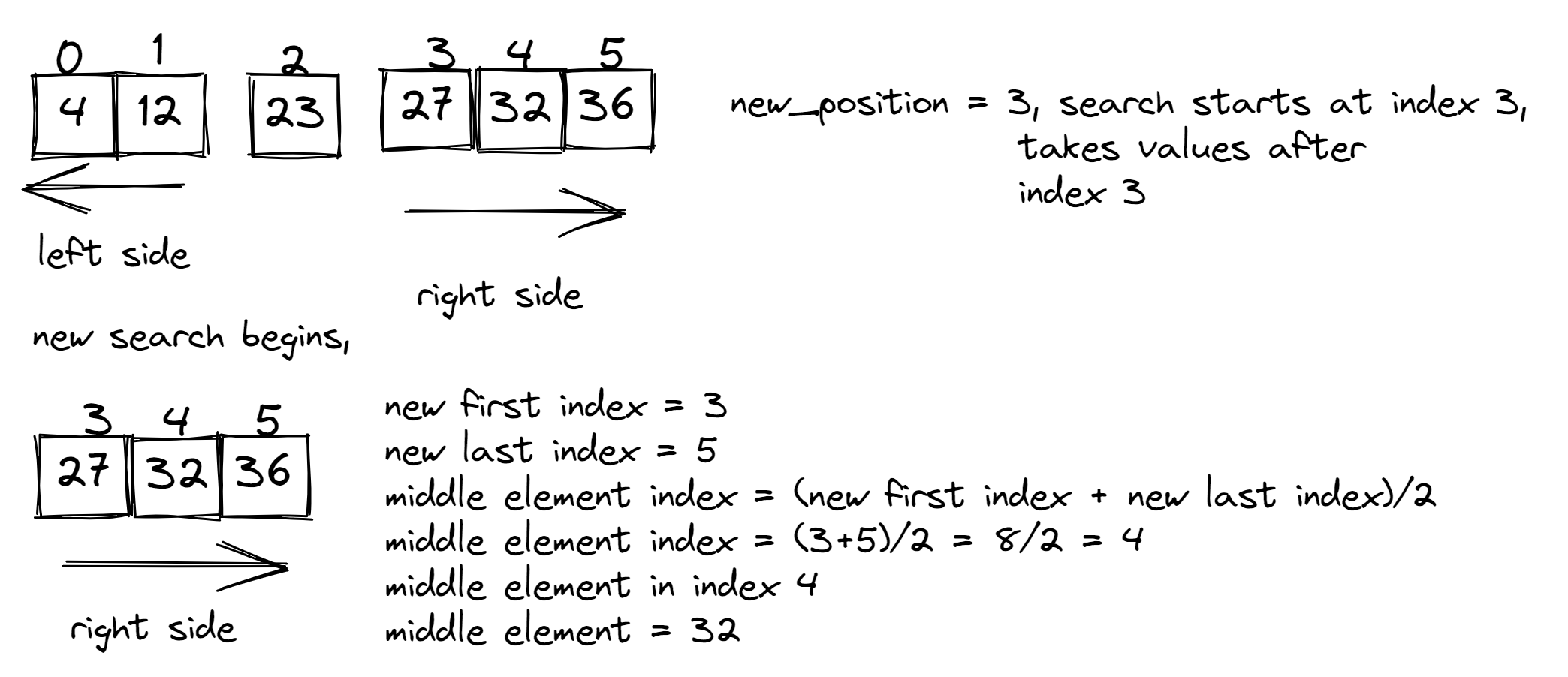
Comparing the middle element (32) to the target value (32), we see they are equal. So the search is terminated and the output is the position "4" occupies in the list (index 4).
Methods Used in Binary Search Algorithms
There are two methods that can implement the “divide and conquer” technique in the search. They are iteration and recursion.
What is Iteration?
In order to get elements from a tuple, list, or dictionary, you iterate through the items with loops.
Iteration is a repeated sequence of statements during execution and it has a countable number of values. For example, when looping through random lists, we loop through the actual variable containing the lists to get the values.
Code implementation for binary search with iteration
Here's the code:
def binary_search(list_num , to_search):
first_index = 0
size = len(list_num)
last_index = size - 1
mid_index = (first_index + last_index) // 2
# print(mid_index)
mid_element = list_num[mid_index]
# print(mid_element)
is_found = True
while is_found:
if first_index == last_index:
if mid_element != to_search:
is_found = False
return " Does not appear in the list"
elif mid_element == to_search:
return f"{mid_element} occurs in position {mid_index}"
elif mid_element > to_search:
new_position = mid_index - 1
last_index = new_position
mid_index = (first_index + last_index) // 2
mid_element = list_num[mid_index]
if mid_element == to_search:
return f"{mid_element} occurs in position {mid_index}"
elif mid_element < to_search:
new_position = mid_index + 1
first_index = new_position
last_index = size - 1
mid_index = (first_index + last_index) // 2
mid_element = list_num[mid_index]
if mid_element == to_search:
return f"{mid_element} occurs in position {mid_index}"
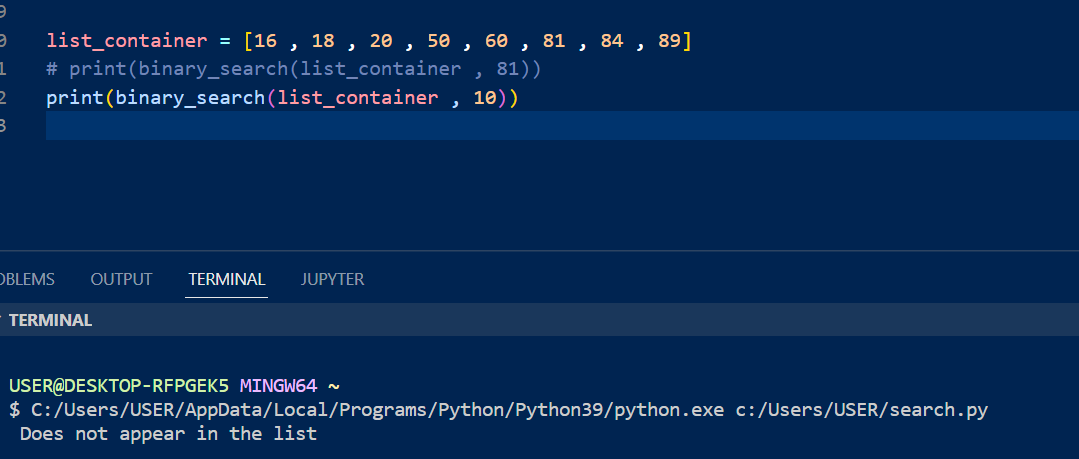
list_container = [16 , 18 , 20 , 50 , 60 , 81 , 84 , 89]
print(binary_search(list_container , 81))
print(binary_search(list_container , 10))
Now let's see what's going on here:
- First, we pass in a list and a value to be searched (to_search) as an input to a function.
- In the function, we create a variable name of first index and assign it to "0". The first index in a list is always "0".
- Then we create four variable names: "size" to store the length of the list, "last_index" to store the index of the last element, "mid_index" to store the operation of finding the middle element index, and "mid_element" to store the middle element gotten from the list using the mid index as position.
- Afterwards, we introduce a while loop to make the conditions run on repeat. Above the while loop we create a variable name "is_found" and set it to "True". This condition checks if the "item to be searched" is found or not.
- In the while loop, we check all the conditions. The first condition is to check if the middle element and the variable "to_search" are equal. If they are equal, the position of the item will be returned.
- Then we check for the second condition (if middle element != item to be searched) which leads us to the two scenarios:
– if the middle element is greater than the item to be searched, the new position will shift to the left once. The search will begin from the first index and end at the new position which is the new last index.
– If the middle element is less than the item to be searched, the new position will shift to the right once. The search will begin from the new position as the new first index and end at the last index.
At the end of these scenarios, we check if the new middle element is the same as the item to be searched. If it is the same, the position of the item will be returned. If not, the conditions are checked until the values are equal.
For error handling, let's say we want to search for a value that does not appear in the list. If we end at the two conditions, the loop will keep running and may eventually crash the system.
To catch the error, we set a condition to check if the first index equals the last index. Then we check if the middle element is equal to the item to be searched. If it is not equal," is found" will be "False". When you run this, it shows an empty array. In my code, the output is a statement.
The final step is to call the function and the result is displayed.
And here are the results:
If the element is in the list, the output is the position.

If the element is not in the list, the output is a statement like this:
What is Recursion?
A function is said to be recursive if it makes reference to itself or previous term(s) to solve a task.
A recursive function is repetitive and it is executed in sequence. It starts from a complex problem and breaks things down into a simpler form.
Code implementation for binary search with recursion
With recursion, it is a bit simpler and requires less code. Here's what it looks like:
def binary_search(list_num, first_index, last_index, to_search):
if last_index >= first_index:
mid_index = (first_index + last_index) // 2
mid_element = list_num[mid_index]
if mid_element == to_search:
return f"{mid_element} occurs in position {mid_index}"
elif mid_element > to_search:
new_position = mid_index - 1
# new last index is the new position
return binary_search(list_num, first_index, new_position, to_search)
elif mid_element < to_search:
new_position = mid_index + 1
# new first index is the new position
return binary_search(list_num, new_position, last_index, to_search)
else:
return " Does not appear in the list"
list_container = [ 1, 9, 11, 21, 34, 54, 67, 90 ]
search = 34
first = 0
last= len(list_container) - 1
print(binary_search(list_container,first,last,search))
- First, a function accepts four inputs: the first index, last index, list, and to_search (item to be searched).
- Then we check if the value of the last index is greater than or equal to the value of the first index. If the condition is true, we assign the operation of finding the middle element index to the variable name "mid_index". Then the middle element is gotten from the list using the mid index as position.
- We create an "if" statement under the first "if" block to check if the middle element and the variable "to_search" are equal. If they are equal, the position of the item will be returned.
- Then we check for the second condition, (if middle element != item to be searched) which leads us to two scenarios:
– if the middle element is greater than the item to be searched, the new position will shift to the left once. The search will begin from the first index and end at the new position. We return the function and pass in the new position as the last index value.
– if the middle element is less than the item to be searched, the new position will shift to the right once. The search will begin from the new position and end at the last index. We return the function and pass in the new position as the first index value. - The last condition will be on the same indent as the first "if" statement. If the to_search is not in the list, it will return a statement
The final step is to call the function and the result is displayed.
And here are the results:
If the element is in the list, the output is the position:
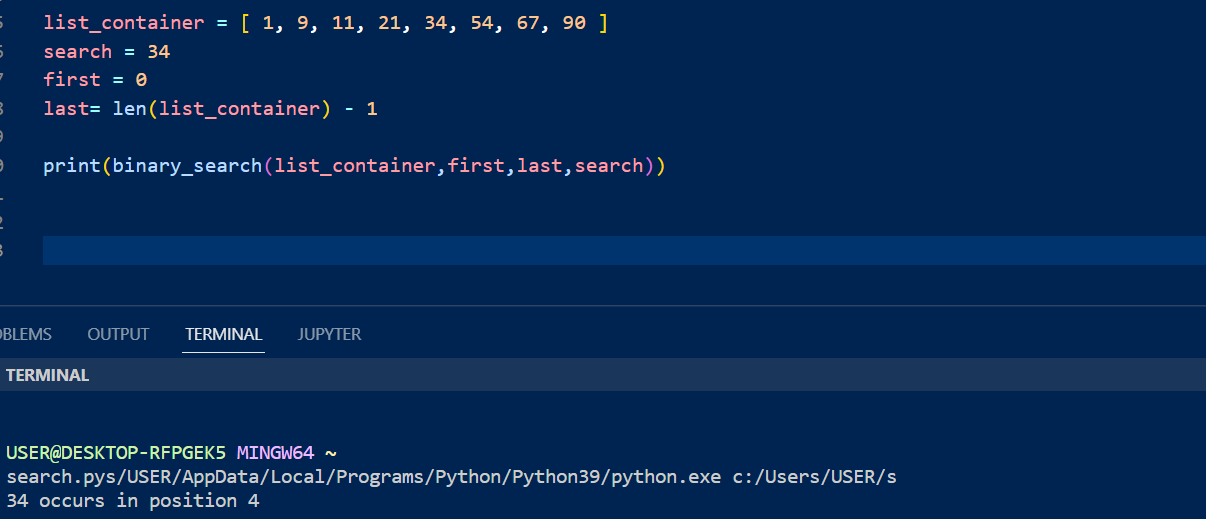
If the element is not in the list, the output is a statement:

Real-life Examples of Binary Search
You might not realize it, but we perform binary search all the time. Here are a few examples of how you might use or encounter it in your daily life or work:
- Searching for a word in a dictionary
- searching for a literature text book in a literature section in a library
- searching for an element in a sorted list
- searching for students taller than 5 feet 3 inches in a line of students arranged according to their heights.
Conclusion
At the end of this article, you should be familiar with how binary search algorithms work and how to implement them in code.
It's fine if you could not grasp everything at once – just give yourself some time and practice. If you encounter any errors or have questions, you can reach out to me on Twitter.

