Binary trees are one of the most complicated data structures out there. And one of the reasons they're so difficult is that it's hard to actually visualize them in a simple way.
In this tutorial, I'll show you how to create your own BinaryTreeViewer which will allow you to watch your trees at runtime.
You can check out the source code of the project here: https://github.com/giladbarilan/binary-tree-viewer
What are Binary Trees?
Binary Trees are a very commonly used data structure that's node-based. Each node of the tree consists of three elements:
- the value of the node,
- a reference to the left child (can be null if it has no left child),
- a reference to the right child (can be null if it has no right child).
For example, let's say we have a node with the value of 1 that has a child on the left with the value of 3 and a child on the right with the value of 2. Here is how we would draw the tree's diagram:
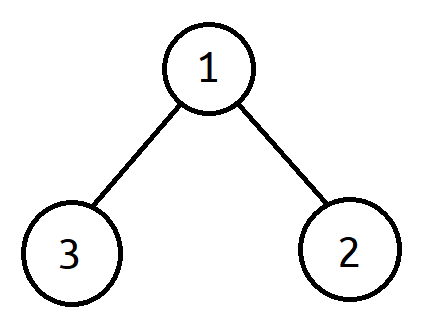
A node can have at most two children, but it can also have one or none. When we want to go through the elements in a binary tree we usually use recursive methods (an example is shown below).
So now that we know how a binary tree data structure works, let's learn how we can implement the binary tree structure in C#.
namespace BinaryTreeViewer
{
/// <summary>
/// Represents a Binary Tree class used for the BinaryTreeViewer.
/// </summary>
/// <typeparam name="T">The tree node's type.</typeparam>
public partial class BinaryTree<T>
{
private BinaryTree<T>? rightNode; // right node of the binary tree.
private BinaryTree<T>? leftNode; // left node of the binary tree.
public T value { get; set; } // the value of the current node.
public BinaryTree(T value)
{
this.value = value;
this.rightNode = null;
this.leftNode = null;
}
public BinaryTree(T value, BinaryTree<T>? left, BinaryTree<T>? right) : this(value)
{
this.rightNode = right;
this.leftNode = left;
}
public void SetLeftNode(BinaryTree<T> node)
{
this.leftNode = node;
}
public void SetRightNode(BinaryTree<T> node)
{
this.rightNode = node;
}
public BinaryTree<T>? GetRightNode() => this.rightNode;
public BinaryTree<T>? GetLeftNode() => this.leftNode;
public override string? ToString() => this.value?.ToString();
}
}In the code above, we built the binary tree structure with the 3 elements we talked about: the value, the right child and the left child. The question mark shows that they are nullable.
Let's make a simple example that demonstrates how to print all of the elements on a Binary Tree.
//Builds the tree.
BinaryTree<int> tree2 = new BinaryTree<int>(1);
tree2.SetRightNode(new BinaryTree<int>(2));
tree2.GetRightNode().SetLeftNode(new BinaryTree<int>(4));
tree2.SetLeftNode(new BinaryTree<int>(3));
tree2.GetLeftNode().SetRightNode(new BinaryTree<int>(5));
PrintTree(tree2);
//Prints out the tree
public static void PrintTree<T>(BinaryTree<T> tree_)
{
if (tree_.GetLeftNode() != null) //if he has a child from his left.
PrintTree(tree_.GetLeftNode()); //go to his left child family.
if (tree_.GetRightNode() != null) //if he has a child from his right.
PrintTree(tree_.GetRightNode()); //go to his right child family.
Console.WriteLine(tree_.value); //print the current value.
}Basic Binary Tree Algorithm
Before we get into the implementation, it's a good idea to start by understanding the algorithm.
So let's go back to our simple example of a tree:
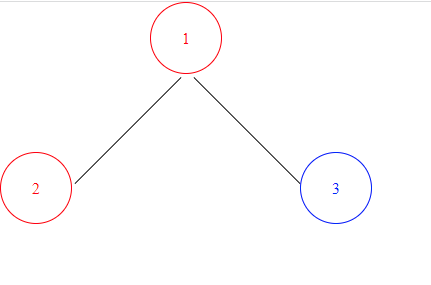
From this little example, we can actually understand the basics of how to build the tree properly.
First of all, it's impossible to predict how much offset we will have to give the parent node (so that there will be enough room to draw the left-most node of the tree). Because of this, we need to first find that left-most node of the tree.
Once we find it, we'll understand how much offset we need to have from the parent of the tree.
In this example, we can't write the parent first because we don't know how many nodes there will be from the left. We might have a problem drawing node 2 if we didn't have any offset on the x-axis when writing node 1.
The Problem with the Binary Tree Algorithm
When we draw the tree, we take a constant distance from the parent node. In the example above, the distance between the parent node to node 3 equals the distance between the parent node to node 2. As a result, this algorithm can run into problems such as the diamond diagram.
What is the Diamond Diagram?
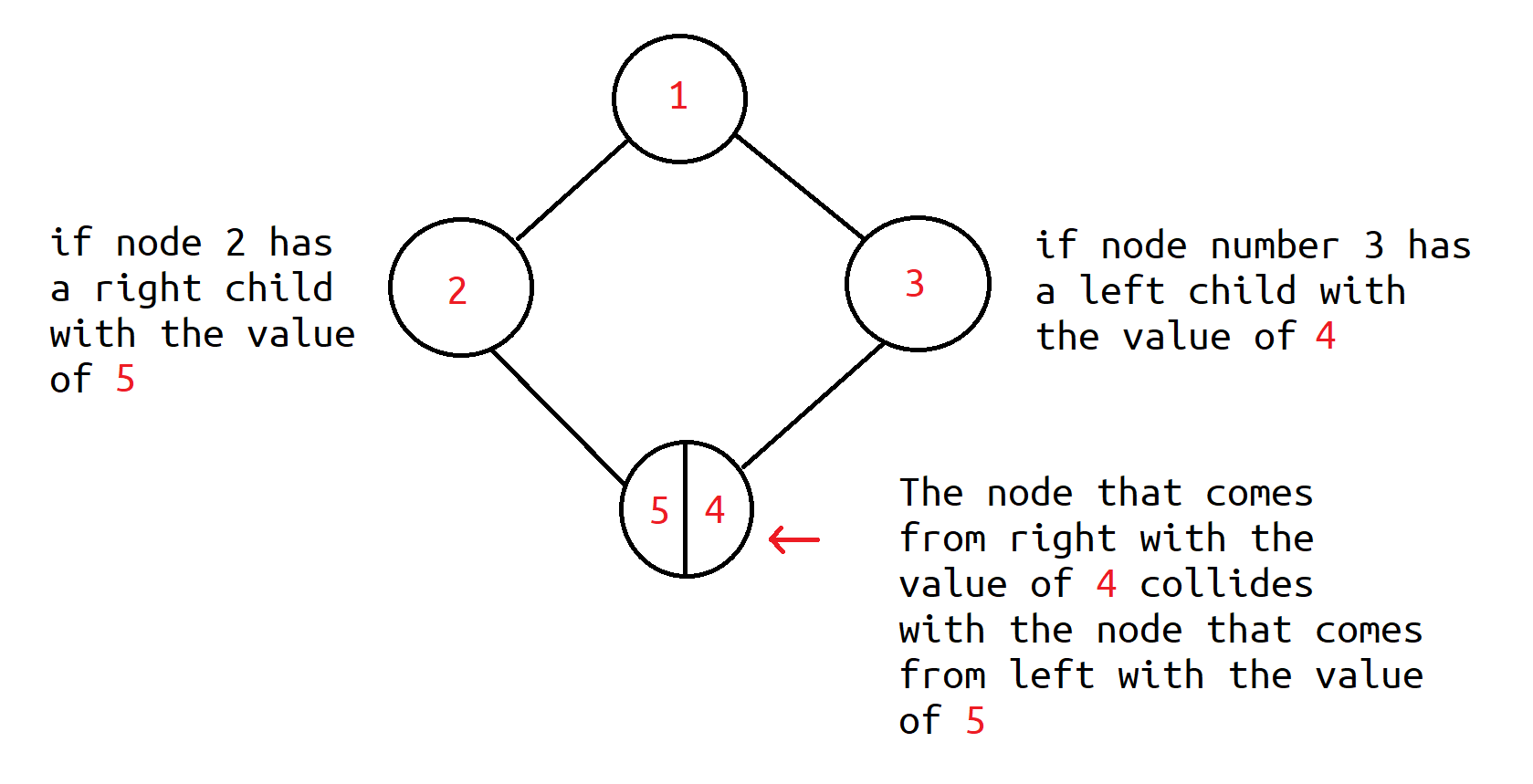
Let's say that the parent node has both left (node 2) and right children (node 3). And the right child (node 3) has a left child (node 4), while the left child (node 2) has a right child (node 5).
In this case, we'll get a collision with the children (node 4 and node 5) because they will be placed at the same position.
Now, there are two main ways to solve this problem:
- Make pre-build calculations that draw the tree as a non-symmetric tree without necessarily constant distances from the parent.
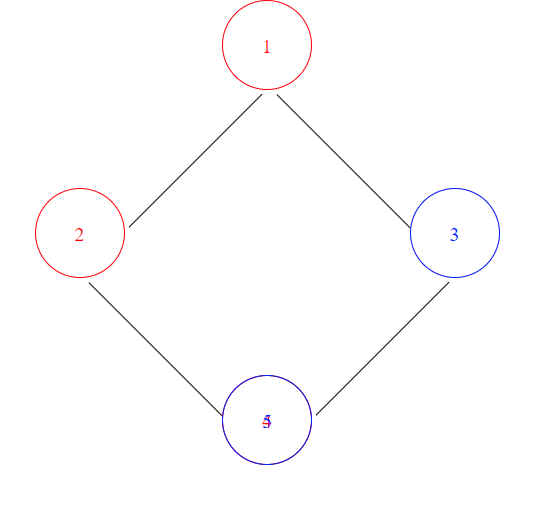
- Color nodes that come from the left in one color, and color nodes that come from right in a different color.
The problem with the first implementation is that we are using the BinaryTreeViewer in order to help save time. And even if it's tidier and more aesthetically pleasing to use this kind of implementation rather than the coloring, the program would be too slow and would hurt our code's performance.
So in this tutorial, we'll stick with the second way of implementing a fix for the diamond diagram problem (coloring).
How to Implement the Algorithm
So now that we've talked about what binary trees are, what their problems are, and what algorithm we'll use in order to solve these problems – it's time to actually implement the algorithm.
NOTE: a partial class is a class that can be written in separated files, and will be combined on compilation.
Let's start with the easiest implementation which is the BinaryTree class.
namespace BinaryTreeViewer
{
/// <summary>
/// Represents a Binary Tree class used for the BinaryTreeViewer.
/// </summary>
/// <typeparam name="T">The tree node's type.</typeparam>
public partial class BinaryTree<T>
{
private BinaryTree<T>? rightNode; // right node of the binary tree.
private BinaryTree<T>? leftNode; // left node of the binary tree.
public T value { get; set; } // the value of the current node.
public BinaryTree(T value)
{
this.value = value;
this.rightNode = null;
this.leftNode = null;
}
public BinaryTree(T value, BinaryTree<T>? left, BinaryTree<T>? right) : this(value)
{
this.rightNode = right;
this.leftNode = left;
}
public void SetLeftNode(BinaryTree<T> node)
{
this.leftNode = node;
}
public void SetRightNode(BinaryTree<T> node)
{
this.rightNode = node;
}
public BinaryTree<T>? GetRightNode() => this.rightNode;
public BinaryTree<T>? GetLeftNode() => this.leftNode;
public override string? ToString() => this.value?.ToString();
}
}In the other part of the partial class, we have some more methods which we'll use for printing the tree.
public partial class BinaryTree<T>
{
private BinaryTree<T>? max_left_node;
/// <summary>
/// Finds the max left offset from the starting node.
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="head">The beginning of the tree we want to draw.</param>
/// <param name="left_offset"></param>
/// <param name="max_offset"></param>
///
internal (BinaryTree<T>?, int max_offset) GetMaxLeft()
{
int max_offset = 0;
GetMaxLeft(this, 0, ref max_offset);
return (max_left_node, max_offset);
}
private void GetMaxLeft(BinaryTree<T> head, int left_offset, ref int max_offset)
{
if (head.GetLeftNode() != null)
{
left_offset += 1;
if(left_offset > max_offset)
{
max_left_node = head.GetLeftNode();
}
GetMaxLeft(head.GetLeftNode(), left_offset, ref max_offset);
}
if (head.GetRightNode() != null)
{
left_offset -= 1;
GetMaxLeft(head.GetRightNode(), left_offset, ref max_offset);
}
if(left_offset > max_offset)
{
max_offset = left_offset;
}
}
}GetMaxLeft
GetMaxLeft is supposed to give us two details we need for the implementation:
- Which node is the left-most node of the tree, and
- How much left offset it has from the parent node (later it will be multiplied by a constant value).
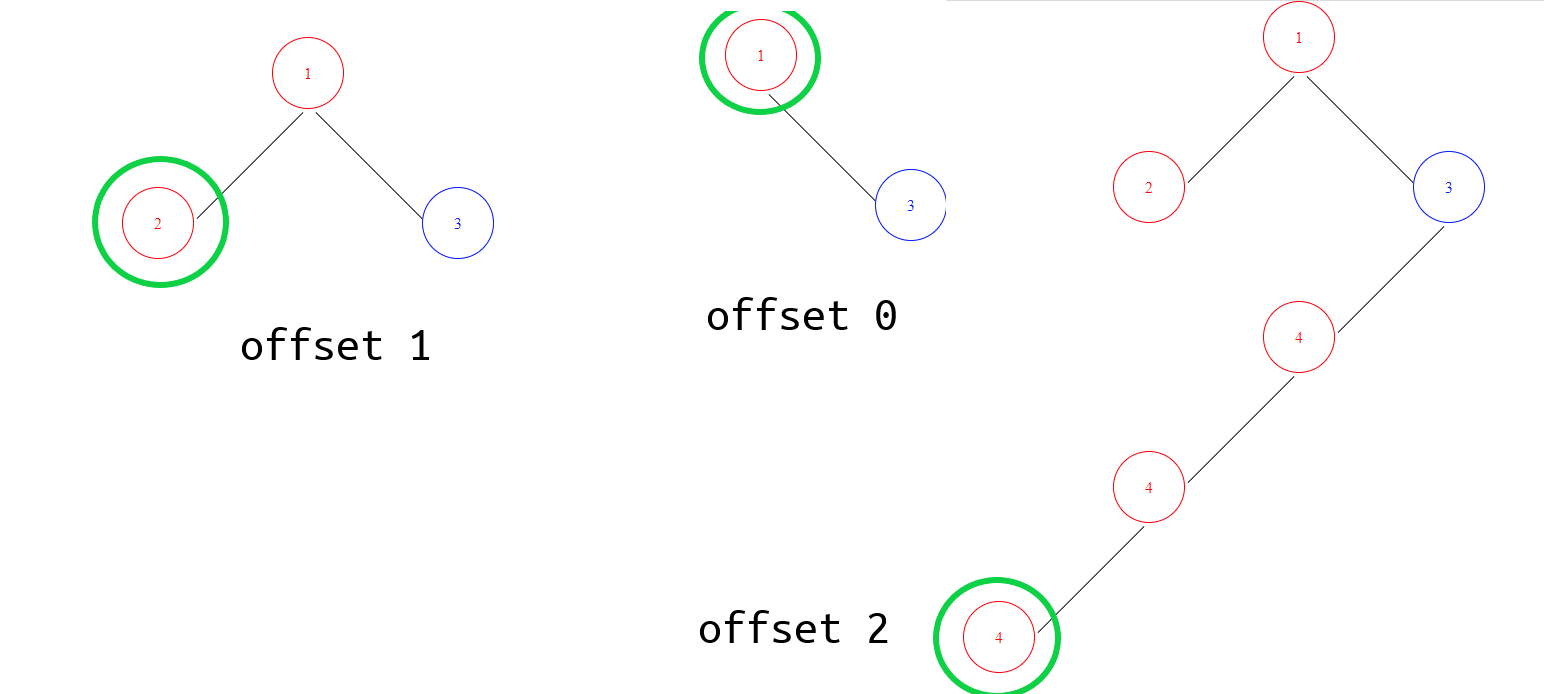
We return the two as a tuple.
How GetMaxLeft works
GetMaxLeft returns the left-most node offset from the parent node of the tree. How does this work?
For every move to a right node, we decrease the left offset value (because we are moving away from the left side of the document). And for every time we go to a left node we increase the offset (because we are getting closer to the left side of the document).
We keep the longest offset from the head we've reached and we set the value of it by reference to the "max_offset" parameter, which we return on the non-recursive GetMaxLeft method.
BTViewer Class
Now that we've gone through the basics, it's time to face the problem we are here to solve, which is how to draw the trees. In the BTViewer class, we manage all of the tree building processes and temporary files.
using System.Diagnostics;
using System.Text.RegularExpressions;
namespace BinaryTreeViewer
{
/// <summary>
/// Shows in an HTML document a graph of the tree.
/// RECOMMENDATION: Use break-point on the line of the BinaryTreeViewer.View .
/// </summary>
public static class BTViewer
{
private static int StartingTempCount = 1; //the starting temp count so we know how many
//trees we've created.
private static int tempCount = 1; // the number of temporary files we've created.
private static readonly string BINTREE_CSS_FILENAME = "BINTREEINITIALIZER.css";
private static string fileName => $"BINTREE{tempCount}.html"; //name structure of BINTREE files.
/// <summary>
/// Sets the value of tempCount according to the previous saved_trees.
/// </summary>
static BTViewer()
{
string directory = Directory.GetCurrentDirectory();
if(!Directory.GetFiles(directory).Contains(BINTREE_CSS_FILENAME))
{
File.WriteAllText(BINTREE_CSS_FILENAME, @"#circle{
border-radius: 50%;
display: inline-block;
border: 1px solid black;
}
.a{
padding: 50px;
}
.b{
width: 70px;
height: 70px;
}
.line{
width: 150px;
height: 150px;
border-bottom: 1px solid black;
position: absolute;
}");
}
Regex reg = new Regex(@"BINTREE\d+\.html"); //we check what is the latest binary tree file.
List<string> fileNames = Directory.GetFiles(directory).ToList();
fileNames = reg.Matches(string.Join(" ", fileNames)).Select(x => x.Value).ToList(); //Get the BINTREE files on the directory.
if (fileNames.Count > 0)
{
//we find the next fileName as -> the latest file name count (BINTREE*Number*) + 1
tempCount = fileNames.Select(x => int.Parse(new Regex(@"\d+").Match(x).Value)).Max() + 1; //the next tree to draw.
}
else
tempCount = 1;
StartingTempCount = tempCount;
}
/// <summary>
/// Writes the full tree into a file by the head.
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="tree">The starting of the tree.</param>
public static void View<T>(BinaryTree<T> tree)
{
// in case they entered invalid tree.
if (tree == null)
return;
// in case there is only one node on the tree (only the head).
if(tree.GetRightNode() == null && tree.GetLeftNode() == null)
{
InitializeFileStructure(); // we initialize the file structure.
DrawElement(tree, (0, 0), false);
File.AppendAllText(fileName, "</html>");
RunTree();
tempCount++;
return;
}
//how much left we take from the beginning (max value). -> max_left_offset
int max_left_offset = tree.GetMaxLeft(); // the max left node.
// we start by finding the position of the head of the tree.
(int x, int y) head_position = (0, 50);
head_position.x = max_left_offset * (100 + 50); //the size of every circle + offset between circles.
InitializeFileStructure();
DrawTree(tree, head_position, false);
File.AppendAllText(fileName, "</html>"); //finishes the document.
RunTree();
tempCount++;
}
/// <summary>
/// Deletes the trees we want to clear.
/// </summary>
public static void ClearTrees(TreesToClear treesToClear)
{
string directory = Directory.GetCurrentDirectory();
Regex reg = new Regex(@"BINTREE\d+\.html"); //the structure of a BINTREE runtime file.
Regex findCount = new Regex(@"\d+");
List<string> fileNames = Directory.GetFiles(directory).ToList();
fileNames = reg.Matches(string.Join(" ", fileNames)).Select(x => x.Value).ToList();
if (((int)treesToClear & 0b1) != 0) //current run.
{
fileNames.Where(x => int.Parse(findCount.Match(x).Value) >= StartingTempCount)
.ToList().ForEach(x => File.Delete(x));
}
if(((int)treesToClear & 0b10) != 0) //other runs.
{
fileNames.Where(x => int.Parse(findCount.Match(x).Value) < StartingTempCount)
.ToList().ForEach(x => File.Delete(x));
}
}
/// <summary>
/// Draws the full tree to the file.
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="head">The head of the tree.</param>
/// <param name="position">The starting position to draw the tree.</param>
private static void DrawTree<T>(BinaryTree<T> head, (int x, int y) position, bool right)
{
DrawElement(head, position, right);
if(head.GetRightNode() != null)
{
DrawLine(position, (position.x + 150, position.y + 150));
DrawTree(head.GetRightNode(), (position.x + 150, position.y + 150), true);
}
if(head.GetLeftNode() != null)
{
DrawLine(position, (position.x - 150, position.y + 150));
DrawTree(head.GetLeftNode(), (position.x - 150, position.y + 150), false);
}
}
/// <summary>
/// Draws line between the nodes.
/// </summary>
/// <param name="p1"></param>
/// <param name="p2"></param>
private static void DrawLine((int x, int y) p1, (int x, int y) p2)
{
double left;
if (p2.x < p1.x)
{
left = Math.Min(p1.x, p2.x);
}
else
{
left = p2.x - 75;
}
string line = $"\n<div class = 'line' style = 'left:{left}px;top:{p1.y}px;transform:rotate({45 * (Math.Sign(p2.x - p1.x))}deg);'></div>";
File.AppendAllText(fileName, line);
}
/// <summary>
/// Draws a node.
/// </summary>
/// <typeparam name="T"></typeparam>
/// <param name="node"></param>
/// <param name="position"></param>
private static void DrawElement<T>(BinaryTree<T> node, (double x, double y) position, bool right)
{
//DIAMOND COLLISION MEANING ->
/*
( )
/ \
( ) ( )
\ /
( ) -> collision (two different nodes placed on the same place in the graph
because the distance between each node to his father is
equal).
*/
//In a case of diamond collision one node might override the other node on a graph.
//Because we want to see both nodes on the graph then we color nodes that
//comes from right and nodes that comes from left
//with two different colors -> Red & Blue -> so we'll be able to see the differences.
string color = "red"; //Red -> left side node, Blue -> right side node.
if (right)
color = "blue";
File.AppendAllText(fileName, $"\n<div class ='b' id = 'circle' style='border: 1px solid {color};position: absolute; left: {position.x}px; top: {position.y}px;'></div>");
File.AppendAllText(fileName, $"\n<div style='color:{color};position: absolute; left: {position.x - (node.ToString().Length / 2) * 4 + 32}px; top: {position.y + 28}px;'>{node.value}</div>");
}
//Opens the tree.
private static void RunTree()
{
//shows the tree to the user. (opens the HTML file on browser).
Process run_process = Process.Start(@"cmd.exe", "/c " + fileName);
run_process.WaitForExit();
}
/// <summary>
/// Creating a BINTREE file structre.
/// </summary>
/// <returns></returns>
private static string InitializeFileStructure()
{
//The basic content of a BINTREE file.
string content = @$"<html><link rel=""stylesheet"" href=""{BINTREE_CSS_FILENAME}"">";
File.WriteAllText(fileName, content);
return fileName;
}
}
}
public enum TreesToClear
{
CurrentRun = 0b1,
PreviousRuns = 0b10
}As you can see, the BTViewer class is long, so let's split it into a couple of parts.
How to Draw the Tree
Now we'll walk through of how to print the tree.
BTViewer.View method
public static void View<T>(BinaryTree<T> tree)
{
// in case they entered invalid tree.
if (tree == null)
return;
// in case there is only one node on the tree (only the head).
if(tree.GetRightNode() == null && tree.GetLeftNode() == null)
{
InitializeFileStructure(); // we initialize the file structure.
DrawElement(tree, (0, 0), false);
File.AppendAllText(fileName, "</html>");
RunTree();
tempCount++;
return;
}
//how much left we take from the beginning (max value). -> max_left_offset
int max_left_offset = tree.GetMaxLeft(); // the max left node.
// we start by finding the position of the head of the tree.
(int x, int y) head_position = (0, 50);
head_position.x = max_left_offset * (100 + 50); //the size of every circle + offset between circles.
InitializeFileStructure();
DrawTree(tree, head_position, false);
File.AppendAllText(fileName, "</html>"); //finishes the document.
RunTree();
tempCount++;
}This method is public for the user and they use this method to print the tree.
In the method, we handle two different cases:
We have only one node in the tree – we simply write the node tree into an HTML file, update the next file number (will be explained later), open the file for preview, and exit from the method.
We have multiple nodes on the tree – in this case, we start by getting data about the left-most node of the tree using the method we explained before. After we collect the data of the left-most node, we can calculate where the head of the tree is supposed to be in the document.
After we've found the starting position of the head of the tree we can start to write the tree from the head.
How Do We Draw the Tree?
Now it's time to go deeper into the drawing implementation. The first method we use is InitializeFileStructure which basically gives us the CSS attributes we need for drawing the circles of the trees.
#circle{
border-radius: 50%;
display: inline-block;
border: 1px solid black;
}
.a{
padding: 50px;
}
.b{
width: 70px;
height: 70px;
}
.line{
width: 150px;
height: 150px;
border-bottom: 1px solid black;
position: absolute;
}The InitializeFileStructure creates an HTML file without </HTML> on purpose because we want to add more tags later for building the tree's structure.
DrawTree method
private static void DrawTree<T>(BinaryTree<T> head, (int x, int y) position, bool right)
{
DrawElement(head, position, right);
if(head.GetRightNode() != null)
{
DrawLine(position, (position.x + 150, position.y + 150));
DrawTree(head.GetRightNode(), (position.x + 150, position.y + 150), true);
}
if(head.GetLeftNode() != null)
{
DrawLine(position, (position.x - 150, position.y + 150));
DrawTree(head.GetLeftNode(), (position.x - 150, position.y + 150), false);
}
}The DrawTree method is a recursive method that is supposed to print all of the lines and circles of the tree.
- At every enter, we print the current element using the DrawElement method.
- Then we move through all of the nodes on the binary tree and set the position of each one by increasing/decreasing a constant value from the previous node.
- We also draw a line from each node to its child using the DrawLine method.
DrawElement method
private static void DrawElement<T>(BinaryTree<T> node, (double x, double y) position, bool right)
{
//DIAMOND COLLISION MEANING ->
/*
( )
/ \
( ) ( )
\ /
( ) -> collision (two different nodes placed on the same place in the graph
because the distance between each node to his father is
equal).
*/
//In a case of diamond collision one node might override the other node on a graph.
//Because we want to see both nodes on the graph then we color nodes that
//comes from right and nodes that comes from left
//with two different colors -> Red & Blue -> so we'll be able to see the differences.
string color = "red"; //Red -> left side node, Blue -> right side node.
if (right)
color = "blue";
File.AppendAllText(fileName, $"\n<div class ='b' id = 'circle' style='border: 1px solid {color};position: absolute; left: {position.x}px; top: {position.y}px;'></div>");
File.AppendAllText(fileName, $"\n<div style='color:{color};position: absolute; left: {position.x - (node.ToString().Length / 2) * 4 + 32}px; top: {position.y + 28}px;'>{node.value}</div>");
}The DrawElement method does a couple of things:
- Determines the color -> the method checks from what node the node came. If the node came from the right we color it blue, but if it came from the left we color it red.
- Using the color and the position we can also add a circle which wraps the value of the node.
- Then we add the value of the node inside the circle.
DrawLine method
private static void DrawLine((int x, int y) p1, (int x, int y) p2)
{
double left;
if (p2.x < p1.x)
{
left = Math.Min(p1.x, p2.x);
}
else
{
left = p2.x - 75;
}
string line = $"\n<div class = 'line' style = 'left:{left}px;top:{p1.y}px;transform:rotate({45 * (Math.Sign(p2.x - p1.x))}deg);'></div>";
File.AppendAllText(fileName, line);
}The DrawLine method simply takes two nodes and draws a line between them. In order to fit the line, we also do some mathematical calculations.
After we've finished building the tree we add the </HTML> to finish the document. Then we call the method RunTree() to open the tree at runtime. We also increase the tempCount by 1 so we'll know what the name of the next file will be.
BINTREE Files
What are BINTREE Files?
The last part of the project consists of managing the HTML files we've created. Each HTML file will follow a name format which will consist of the name BINTREE. Then we'll add the chronological ID and then the extension of the file.
For instance:
BINTREE1.html
BINTREE2.html
...
BINTREE143.html
BINTREE144.htmlThe ID of the next HTML file we'll create will be equal to the last file name ID number + 1.
- The ID's starts from 1 -> the first BINTREE we'll create will be "BINTREE1.html".
How to Manage the BINTREE Files
The Static Constructor of BTViewer
static BTViewer()
{
string directory = Directory.GetCurrentDirectory();
if(!Directory.GetFiles(directory).Contains(BINTREE_CSS_FILENAME))
{
File.WriteAllText(BINTREE_CSS_FILENAME, @"#circle{
border-radius: 50%;
display: inline-block;
border: 1px solid black;
}
.a{
padding: 50px;
}
.b{
width: 70px;
height: 70px;
}
.line{
width: 150px;
height: 150px;
border-bottom: 1px solid black;
position: absolute;
}");
}
Regex reg = new Regex(@"BINTREE\d+\.html"); //we check what is the latest binary tree file.
List<string> fileNames = Directory.GetFiles(directory).ToList();
fileNames = reg.Matches(string.Join(" ", fileNames)).Select(x => x.Value).ToList(); //Get the BINTREE files on the directory.
if (fileNames.Count > 0)
{
//we find the next fileName as -> the latest file name count (BINTREE*Number*) + 1
tempCount = fileNames.Select(x => int.Parse(new Regex(@"\d+").Match(x).Value)).Max() + 1; //the next tree to draw.
}
else
tempCount = 1;
StartingTempCount = tempCount;
}Because we name them in chronological order we cannot start giving names randomly. This might override other BINTREE files that were already created. That's why we use Regular Expressions in order to find all of the BINTREE files.
Then we take the maximum ID we can find there and we'll increase it by one. The new value will become the beginning of the BINTREE file's ID on this run.
For instance, if we run the program twice and on the first run we've created 5 BINTREE files, this means that our tempCount on the next run will start from 6 and the next file we will create will be BINTREE6.html.
Another job of the static constructor is to check that we have a BINTREEINITIALIZER.css file. If we don't have one, then we need to recreate that. (BINTREEINITIALIZER.css is the CSS file we use for the binary tree style.)
We also save the tempCount in a different field which is StartingTempCount so we'll know with what ID we started writing the trees (we'll use this feature later).
ClearTrees method
The ClearTrees method allows us to delete the temporary BINTREE files we've created during the current run and previous runs. The method accepts an enum value indicating what do we want to delete. The method has 3 options to accept:
BTViewer.ClearTrees(TreesToClear.CurrentRun); //CLEAR ONLY CURRENT RUN
BTViewer.ClearTrees(TreesToClear.PreviousRuns); //CLEAR ONLY PREVIOUS RUNS
BTViewer.ClearTrees(TreesToClear.PreviousRuns | TreesToClear.CurrentRun); //CLEAR ALLpublic static void ClearTrees(TreesToClear treesToClear)
{
string directory = Directory.GetCurrentDirectory();
Regex reg = new Regex(@"BINTREE\d+\.html"); //the structure of a BINTREE runtime file.
Regex findCount = new Regex(@"\d+");
List<string> fileNames = Directory.GetFiles(directory).ToList();
fileNames = reg.Matches(string.Join(" ", fileNames)).Select(x => x.Value).ToList();
if (((int)treesToClear & 0b1) != 0) //current run.
{
fileNames.Where(x => int.Parse(findCount.Match(x).Value) >= StartingTempCount)
.ToList().ForEach(x => File.Delete(x));
}
if(((int)treesToClear & 0b10) != 0) //other runs.
{
fileNames.Where(x => int.Parse(findCount.Match(x).Value) < StartingTempCount)
.ToList().ForEach(x => File.Delete(x));
}
}The method uses Regular Expressions to get all of the BINTREE files we have. And it uses another Regular Expression to get the ID from every BINTREE file we have.
For current run -> we delete all of the files that are greater than or equal to the StartingTempCount which is the ID of the first file we've created during the current run of the program.
For previous runs -> we do the opposite from the current run: we delete all of the files with a lower ID than the ID of the first file we created on this run.
Wrapping Up
Congrats! You are now able to create your own BinaryTreeViewer system. I hope this article helped you understand Binary Trees more clearly.

