How to Build a Linear Regression Model – Machine Learning Example

Ever since the launch of OpenAI's ChatGPT, everyone wants to learn about AI and ML.

Not only that – everyone wants to build and release an AI product on their own to mark their position in the global competition.

And if you already own a SaaS product, you may want to integrate AI and ML features into it to retain your customers and be competitive in the global market.

In this tutorial, you'll learn how to build a Linear Regression Model. This is one of the first things you'll learn how to do when studying Machine Learning, so it'll help you take your first step into this competitive market.

Table of Contents

• Prerequisites
• What is Linear Regression?
• Evaluation Metrics
• Linear Regression Example – Car Price Prediction Model
• How to Build the Model
• Conclusion

Prerequisites

1. Medium level experience using an IDE (preferably VS Code)
2. Basic understanding of Python Notebook (.pynb) files
3. Good understanding of the Python programming language
4. Basic knowledge of Pandas (to handle dataframes), Numpy, Scikit Learn, and Matplot libraries
5. Some knowledge of statistics is helpful for analyzing the data

What is Linear Regression?

Linear Regression is a Supervised Learning method, where the predicted output will be continuous in nature. For example, things like price prediction, marks prediction, and so on.

Linear Regression is a fundamental statistical and machine learning technique used for modeling the relationship between a dependent variable (also known as the target or response variable) and one or more independent variables (predictors or features).

It aims to establish a linear equation that best represents the association between these variables, allowing us to make predictions and draw insights from the data.

The primary goal of linear regression is to find the "best-fit" line (or hyperplane in higher dimensions) that minimizes the difference between the predicted values and the actual observed values.

This best-fit line is defined by a linear equation of the form:

Y = b0 ​+ b1​X1 ​+ b2​X2 ​+...+ bn​Xn​

In this equation:

1. Y represents the dependent variable we want to predict.
2. X1,X2,...,Xn are the independent variables or features.
3. b0 is the intercept (the value of Y when all X values are zero).
4. b1,b2,...,bn are the coefficients that determine the relationship between each independent variable and the dependent variable.

Linear regression assumes that there is a linear relationship between the predictors and the target variable.

The goal of the model is to estimate the coefficients (b0,b1,...,bn) that minimize the sum of the squared differences between the predicted values and the actual values in the training data. This process is often referred to as "fitting the model."

Evaluation Metrics

The evaluation metrics for a Linear Regression model are:

1. Coefficient of Determination or R-Squared (R2)
2. Root Mean Squared Error (RSME)

Let's see what each of these are.

R-Squared

R-Squared describes the amount of variation that is captured by the developed model. It always ranges between 0 and 1. The higher the value of R-squared, the better the model fits with the data.

Root Mean Squared Error

RMSE measures the average magnitude of the errors or residuals between the predicted values generated by a model and the actual observed values in a dataset. It always ranges between 0 and positive infinity. Lower RMSE values indicate better predictive performance.

Linear Regression Example – Car Price Prediction Model

In this example, we'll try to predict the car price by building a Linear Regression model. I found this problem and the dataset in Kaggle. I noticed that there's a submission for this problem, which was perfect. In fact I built my solution by taking a part of that solution.

Let's dive into the problem.

We're given a dataset of used cars, which contains the name of the car, year, selling price, present price, number of kilometers it has driven, type of fuel, type of the seller, transmission, and if the seller is the owner. Our goal is to predict the selling price of the car.

Let's explore the solution.

Import the required packages:

You'll need various packages to work through this problem. Here's how you can import them all:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
from sklearn import metrics
from sklearn.model_selection import KFold
from sklearn.pipeline import make_pipeline
from statsmodels.stats.diagnostic import normal_ad
from statsmodels.stats.outliers_influence import variance_inflation_factor
from statsmodels.stats.stattools import durbin_watson
from scipy import stats

Import the dataset

You can download the dataset (car data.csv) from Kaggle or you can download it from my Github repo.

df = pd.read_csv('./car data.csv')

Pre-process the dataset

The below code shows the columns and their datatype and the number of rows. Our dataset has 9 columns and 301 rows.

df.info()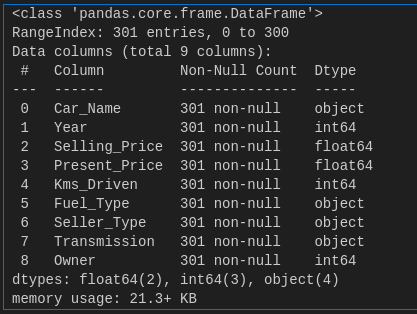

The "Car_Name" column describes the car name. This field should be ignored from our dataset. This is because, only the features of the car matters and not its name.

The below code returns the number of unique car names in our dataset.

df['Car_Name'].nunique()

We have 98 unique car names in our dataset.

Clearly, it does not add any meaning to our dataset, since there are so many categories. Let's drop that column.

df.drop('Car_Name', axis=1, inplace=True)

The dataset has the column named "Year". Ideally, we need the age of car over the year it was bought / sold. So, let's convert that to "Age" and remove the "Year" column.

df.insert(0, "Age", df["Year"].max()+1-df["Year"] )
df.drop('Year', axis=1, inplace=True)

"Age" is calculated by finding the difference between the maximum year available in our dataset and the year of that particular car. This is because, our calculations will be specific to that particular time period and to this dataset.

How to find outliers

An outlier is a data point that differs significantly from other observations. They can cause the performance of the model to drop.

Categorical columns will have the datatype as "object". Let's group the numerical columns and categorical columns in a NumPy array. The first 5 elements in the array will be numerical columns and the rest 3 will be categorical columns.

We can plot the data in the columns using the seaborn library. Categorical columns will contain multiple bars, whereas numerical columns will contain single bars.

Let's try to find the outliers in our dataset using the following code:

sns.set_style('darkgrid')
colors = ['#0055ff', '#ff7000', '#23bf00']
CustomPalette = sns.set_palette(sns.color_palette(colors))

OrderedCols = 
np.concatenate([df.select_dtypes(exclude='object').columns.values,  df.select_dtypes(include='object').columns.values])

fig, ax = plt.subplots(2, 4, figsize=(15,7),dpi=100)

for i,col in enumerate(OrderedCols):
    x = i//4
    y = i%4
    if i<5:
        sns.boxplot(data=df, y=col, ax=ax[x,y])
        ax[x,y].yaxis.label.set_size(15)
    else:
        sns.boxplot(data=df, x=col, y='Selling_Price', ax=ax[x,y])
        ax[x,y].xaxis.label.set_size(15)
        ax[x,y].yaxis.label.set_size(15)

plt.tight_layout()    
plt.show()

Let's try to find the outliers using the InterQuartile Range rule.

This is based on the concept of quartiles, which divide a dataset into four equal parts. The IQR (InterQuartile Range rule) rule specifically focuses on the range of values within the middle 50% of the data and uses this range to identify potential outliers.

We have to find the minimum and maximum quantile values for each unique value in the categorical columns and filter the outlier samples which do not fit into the 25th and 75th percentile of our target column (Selling Price).

On the other hand, the outliers in numerical columns can be filtered by the 25th and 75th percentiles of the same column. We don't need to filter out with respect to the target column.

outliers_indexes = []
target = 'Selling_Price'

for col in df.select_dtypes(include='object').columns:
    for cat in df[col].unique():
        df1 = df[df[col] == cat]
        q1 = df1[target].quantile(0.25)
        q3 = df1[target].quantile(0.75)
        iqr = q3-q1
        maximum = q3 + (1.5 * iqr)
        minimum = q1 - (1.5 * iqr)
        outlier_samples = df1[(df1[target] < minimum) | (df1[target] > maximum)]
        outliers_indexes.extend(outlier_samples.index.tolist())
        
        
for col in df.select_dtypes(exclude='object').columns:
    q1 = df[col].quantile(0.25)
    q3 = df[col].quantile(0.75)
    iqr = q3-q1
    maximum = q3 + (1.5 * iqr)
    minimum = q1 - (1.5 * iqr)
    outlier_samples = df[(df[col] < minimum) | (df[col] > maximum)]
    outliers_indexes.extend(outlier_samples.index.tolist())
    
outliers_indexes = list(set(outliers_indexes))
print('{} outliers were identified, whose indices are:\n\n{}'.format(len(outliers_indexes), outliers_indexes))

By running the above code, we found that there are 38 outliers in our dataset.

But keep in mind that it's not always the right decision to remove the outliers. They can be legitimate observations and it’s important to investigate the nature of the outlier before deciding whether to drop it or not.

We can delete outliers in two cases:

1. Outlier is due to incorrectly entered or measured data
2. Outlier creates a significant association

Let's dig even more and find the perfect outliers.

To do that, let's assume that if the selling price is more than 33 Lakhs or if the car has been driven more than 400,000 Kilometers, those are outliers. We'll mark them in green. Save all the indices in the removing_indices variable. Plot them in the scatterplot format using seaborn library, comparing each column against our target column.

# Outliers Labeling
df1 = df.copy()
df1['label'] = 'Normal'
df1.loc[outliers_indexes,'label'] = 'Outlier'

# Removing Outliers
removing_indexes = []
removing_indexes.extend(df1[df1[target]>33].index)
removing_indexes.extend(df1[df1['Kms_Driven']>400000].index)
df1.loc[removing_indexes,'label'] = 'Removing'

# Plot
target = 'Selling_Price'
features = df.columns.drop(target)
colors = ['#0055ff','#ff7000','#23bf00']
CustomPalette = sns.set_palette(sns.color_palette(colors))
fig, ax = plt.subplots(nrows=3 ,ncols=3, figsize=(15,12), dpi=200)

for i in range(len(features)):
    x=i//3
    y=i%3
    sns.scatterplot(data=df1, x=features[i], y=target, hue='label', ax=ax[x,y])
    ax[x,y].set_title('{} vs. {}'.format(target, features[i]), size = 15)
    ax[x,y].set_xlabel(features[i], size = 12)
    ax[x,y].set_ylabel(target, size = 12)
    ax[x,y].grid()

ax[2, 1].axis('off')
ax[2, 2].axis('off')
plt.tight_layout()
plt.show()

Let's see the perfect outliers:

removing_indexes = list(set(removing_indexes))
removing_indexes

We got 2. We have to remove them. But before that, we have to check if there's any null data in our dataset.

df.isnull().sum()

There are no null values in our dataset.

Let's remove the identified outliers and reset the index of the dataframe.

df1 = df.copy()
df1.drop(removing_indexes, inplace=True)
df1.reset_index(drop=True, inplace=True)

Analyze the Dataset

Let's analyze the data to see how much each field/category is correlated with the selling price of the car. We need to do some analysis on our dataset to be able to come to some conclusions about it.

To do that, we have to identify the numerical and categorical fields in our dataset, as the way to plot this differs for each type.

NumCols = ['Age', 'Selling_Price', 'Present_Price', 'Kms_Driven', 'Owner']
CatCols = ['Fuel_Type', 'Seller_Type', 'Transmission']

Bivariate Analysis

If you're not familiar what bivariate analysis is, here's a basic definition:

Bivariate analysis is one of the simplest forms of quantitative analysis. It involves the analysis of two variables, for the purpose of determining the empirical relationship between them. Bivariate analysis can be helpful in testing simple hypotheses of association.

Let's compare the Selling Price with the other columns using Bivariate Analysis and try to derive some conclusions out of that data.

Selling Price vs Numerical Features Bivariate Analysis

Let's compare the numerical features with the Selling Price using Bivariate analysis. The Numerical columns will be plotted in a scatter graph.

fig, ax = plt.subplots(nrows=2 ,ncols=2, figsize=(10,10), dpi=90)
num_features = ['Present_Price', 'Kms_Driven', 'Age', 'Owner']
target = 'Selling_Price'
c = '#0055ff'

for i in range(len(num_features)):
    row = i//2
    col = i%2
    ax[row,col].scatter(df1[num_features[i]], df1[target], color=c, edgecolors='w', linewidths=0.25)
    ax[row,col].set_title('{} vs. {}'.format(target, num_features[i]), size = 12)
    ax[row,col].set_xlabel(num_features[i], size = 12)
    ax[row,col].set_ylabel(target, size = 12)
    ax[row,col].grid()

plt.suptitle('Selling Price vs. Numerical Features', size = 20)
plt.tight_layout()
plt.show()

Selling Price vs Categorical Features Bivariate Analysis

Let's compare the categorical features with the Selling Price using Bivariate analysis. The Categorical columns will be plotted in a stripplot graph. This gives the comparison among multiple values in a category.

fig, axes = plt.subplots(nrows=1 ,ncols=3, figsize=(12,5), dpi=100)
cat_features = ['Fuel_Type', 'Seller_Type', 'Transmission']
target = 'Selling_Price'
c = '#0055ff'

for i in range(len(cat_features)):
    sns.stripplot(ax=axes[i], x=cat_features[i], y=target, data=df1, size=6, color=c)
    axes[i].set_title('{} vs. {}'.format(target, cat_features[i]), size = 13)
    axes[i].set_xlabel(cat_features[i], size = 12)
    axes[i].set_ylabel(target, size = 12)
    axes[i].grid()

plt.suptitle('Selling Price vs. Categorical Features', size = 20)
plt.tight_layout()
plt.show()

Here are the conclusions we can make from our data analysis:

1. As Present Price increases, Selling Price increases as well. They're directly proportional.
2. Selling Price is inversely proportional to Kilometers Driven.
3. Selling Price is inversely proportional to the car's age.
4. As the number of previous car owners increases, its Selling Price decreases. So Selling Price is inversely proportional to Owner.
5. Diesel Cars > CNG Cars > Petrol Cars in terms of Selling Price.
6. The Selling Price of cars sold by individuals is lower than the price of cars sold by dealers.
7. Automatic cars are more expensive than manual cars.

Categorical Variables Encoding

We can't use the Categorical fields as they are. They have to be converted to numbers because machines can only understand numbers.

For an example, let's take the Fuel column. As per our dataset, we have cars running on two types of fuel. They are Petrol and Diesel. The categorical variable encoding will split the fuel column into 2 columns (Fuel_Type_Petrol and Fuel_Type_Diesel).

Let's assume a car runs on Petrol. For this car, the data will be converted as Fuel_Type_Petrol column set to 1 (True), and Fuel_Type_Diesel column set to 0 (False). Computers can understand 1 and 0 rather than "Petrol" and "Diesel".

To do that, we'll perform one-hot encoding for the categorical columns. Pandas offers the get_dummies method to encode the columns.

CatCols = ['Fuel_Type', 'Seller_Type', 'Transmission']

df1 = pd.get_dummies(df1, columns=CatCols, drop_first=True)
df1.head(5)

Assume True and False are 0 and 1, respectively.

Correlation Analysis

A correlation matrix is a matrix that summarizes the strength and direction of the linear relationships between pairs of variables in a dataset. It is a crucial tool in statistics and data analysis, used to examine the patterns of association between variables and understand how they may be related.

The correlation is directly proportional if the values are positive, and inversely proportional if the values are negative.

Here's the code to find the correlation matrix with relation to Selling Price.

target = 'Selling_Price'
cmap = sns.diverging_palette(125, 28, s=100, l=65, sep=50, as_cmap=True)
fig, ax = plt.subplots(figsize=(9, 8), dpi=80)
ax = sns.heatmap(pd.concat([df1.drop(target,axis=1), df1[target]],axis=1).corr(), annot=True, cmap=cmap)
plt.show()

From the above matrix, we can infer that the target variable "Selling Price" is highly correlated with Present Price, Seller Type, and Fuel Type.

How to Build the Model

We have come to the final stage. Let's train and test our model.

Let's remove the "Selling_Price" from input and set it to output. This means that it has to be predicted.

X = df1.drop('Selling_Price', axis=1)
y = df1['Selling_Price']

Let's split our dataset by taking 70% of data for training and 30% of data for testing.

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)

Let's make a backup of our test data. We need this for the final comparison.

y_test_actual = y_test

Normalize the dataset

The StandardScaler is a preprocessing technique commonly used in machine learning and data analysis to standardize or normalize the features (variables) of a dataset. Its primary purpose is to transform the data such that each feature has a mean (average) of 0 and a standard deviation of 1.

Let's normalize our dataset using StandardScaler.

scaler = StandardScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
X_test_scaled = scaler.transform(X_test)

It is very important that StandardScaler transformation should only be gotten from the training set, otherwise it will lead to data leakage.

Train the model

linear_reg = LinearRegression()
linear_reg.fit(X_train_scaled, y_train)

Let's find the intercept and co-efficient for each column in our training dataset.

pd.DataFrame(data = np.append(linear_reg.intercept_ , linear_reg.coef_), index = ['Intercept']+[col+" Coef." for col in X.columns], columns=['Value']).sort_values('Value', ascending=False)

How to evaluate the model

Scikit Learn provides a metrics feature which helps us to measure the metrics of our model. We can use that to determine metrics include Mean Squared Error, Mean Absolute Error, Root Mean Squared Error, and R2-Score.

Now it's time to evaluate the model:

def model_evaluation(model, X_test, y_test, model_name):
    y_pred = model.predict(X_test)
    
    MAE = metrics.mean_absolute_error(y_test, y_pred)
    MSE = metrics.mean_squared_error(y_test, y_pred)
    RMSE = np.sqrt(MSE)
    R2_Score = metrics.r2_score(y_test, y_pred)
    
    return pd.DataFrame([MAE, MSE, RMSE, R2_Score], index=['MAE', 'MSE', 'RMSE' ,'R2-Score'], columns=[model_name])

model_evaluation(linear_reg, X_test_scaled, y_test, 'Linear Reg.')

Evaluate the model using K-fold Cross-Validation

In k-fold cross-validation, the dataset is divided into k roughly equal-sized subsets or "folds." The model is trained and evaluated k times, each time using a different fold as the validation set and the remaining folds as the training set.

The results (for example accuracy, error) of these k runs are then averaged to obtain a more robust estimate of the model's performance.

The advantage is that each data point is used for both training and validation, reducing the risk of bias in the evaluation.

linear_reg_cv = LinearRegression()
scaler = StandardScaler()
pipeline = make_pipeline(StandardScaler(),  LinearRegression())

kf = KFold(n_splits=6, shuffle=True, random_state=0) 
scoring = ['neg_mean_absolute_error', 'neg_mean_squared_error', 'neg_root_mean_squared_error', 'r2']
result = cross_validate(pipeline, X, y, cv=kf, return_train_score=True, scoring=scoring)

MAE_mean = (-result['test_neg_mean_absolute_error']).mean()
MAE_std = (-result['test_neg_mean_absolute_error']).std()
MSE_mean = (-result['test_neg_mean_squared_error']).mean()
MSE_std = (-result['test_neg_mean_squared_error']).std()
RMSE_mean = (-result['test_neg_root_mean_squared_error']).mean()
RMSE_std = (-result['test_neg_root_mean_squared_error']).std()
R2_Score_mean = result['test_r2'].mean()
R2_Score_std = result['test_r2'].std()

pd.DataFrame({'Mean': [MAE_mean,MSE_mean,RMSE_mean,R2_Score_mean], 'Std': [MAE_std,MSE_std,RMSE_std,R2_Score_std]},
             index=['MAE', 'MSE', 'RMSE' ,'R2-Score'])

Results Visualization

Let's create a dataframe with the actual and predicted values.

y_test_pred = linear_reg.predict(X_test_scaled)
df_comp = pd.DataFrame({'Actual':y_test_actual, 'Predicted':y_test_pred})

Let's compare the actual and predicted target values for the test data with the help of a bar plot.

def compare_plot(df_comp):
    df_comp.reset_index(inplace=True)
    df_comp.plot(y=['Actual','Predicted'], kind='bar', figsize=(20,7), width=0.8)
    plt.title('Predicted vs. Actual Target Values for Test Data', fontsize=20)
    plt.ylabel('Selling_Price', fontsize=15)
    plt.show()

compare_plot(df_comp)

In the above graph, the blue lines indicates the actual price and orange lines indicate the predicted price of the cars. You can see that some predicted values are negative. But in most of our cases, our model has predicted it pretty well.

This is not the perfect model. But if you want to fine tune it to make better predictions, let me know via my email. I'll write a tutorial about that if I receive more requests.

Conclusion

In this tutorial, you learned about Linear Regression with a practical example. I hope it helps you to make progress in your ML journey. You can access the above dataset and the code for it in from this Github repo.

Hope you enjoyed reading this article. If you wish to learn more about artificial intelligence / machine learning / deep learning, subscribe to my article by visiting my site which has a consolidated list of all my blogs.