If you're regularly confronted by the complexity of modern data, you’re not alone. In our data-centric world, understanding data structures isn’t optional — it’s essential.
Whether you’re a novice coder or an experienced developer, this handbook is your concise guide to the critical skill of data management through data structures.
Data today isn’t just vast – it’s also complex. Organizing, retrieving, and manipulating this data efficiently is key. Enter data structures — the backbone of effective data management.
This guide cuts through the complexity of arrays, linked lists, stacks, queues, trees, and graphs. You’ll gain insights into each type’s strengths, limitations, and practical applications, backed by real-world examples.
Even the big brains at places like MIT and Stanford say knowing your data structures is super important for making great software. And here, I'll share real-life case studies showing you how these data structures are used in everyday situations.
Ready to dive in? We're going to explore the world of data structures together. You'll find out how to make your data work smarter, not harder, and give yourself an edge in the tech world.
Here’s the awesome journey you’re about to embark on:
- Land Your Dream Tech Job: Imagine walking into big names like Google or Apple with confidence. Your new skills in data structures could be your golden ticket to these tech havens, where knowing your stuff really matters.
- Make Shopping Online a Breeze: Ever wonder how Amazon makes shopping so smooth? With your skills, you could be the wizard behind faster, smarter shopping experiences.
- Be a Financial Whiz: Banks and finance companies love quick, error-free data handling. Your know-how could make you a star in places like Visa or PayPal, keeping money moving swiftly and safely.
- Revolutionize Healthcare: In the world of health, like at Mayo Clinic or Pfizer, your ability to manage data could speed up lifesaving decisions. You could be part of a team that’s changing lives every day.
- Level Up Gaming Experiences: Got a passion for gaming? Companies like Nintendo or Riot Games are always on the lookout for talent that can make games even more thrilling. That could be you.
- Transform Shipping and Travel: Imagine helping FedEx or Delta Airlines move things faster and smarter around the globe.
- Shape the Future with AI: Dream of working with Generative AI? Your understanding of data structures is crucial. You could be part of groundbreaking work at places like OpenAI, Google, Netflix, Tesla or SpaceX, making the stuff of science fiction real.
Upon completing this journey, your grasp of data structures will extend far beyond mere understanding. You'll be equipped to apply them effectively.
Imagine enhancing app performance, devising solutions for business challenges, or even playing a role in pioneering tech advancements. Your newfound skills will open doors to diverse opportunities, positioning you as a go-to problem solver.
Table Of Contents
- The Importance of Data Structures
- Types of Data Structures
- Array Data Structure
- Single-linked List Data Structure
- Double-linked List Data Structure
- Stack Data Structure
- Queue Data Structure
- Tree Data Structure
- Graph Data Structure
- Hash Table Data Structure
- How to Unleash the Power of Data Structures in Programming
- How to Choose the Right Data Structure for Your Application
- How to Efficiently Implement Data Structures
- Common Data Structure Operations and Their Time Complexities
- Real-World Examples of Data Structures in Action
- Resources and Tools for Learning Data Structures
- Conclusion and Next Steps

1. The Importance of Data Structures
Learning about data structures can really help you power-up your software engineering skills. These critical components are key to ensuring your applications operate flawlessly, which is a must-have ability for every software engineer.
They Enhance Efficiency and Performance
Data structures are the turbochargers of your code. They do more than just store data – they enable swift and efficient access. Think of a hash table as your instant-access tool for speedy data retrieval or the linked list as your dynamic, adaptable strategy for evolving data needs.
They Optimize Memory Use and Management
These structures are really good at optimizing memory. They fine-tune your program’s memory consumption, ensuring robustness under heavy data loads and helping you avoid common issues like memory leaks.
They Boost Problem-Solving and Algorithm Design
Data structures elevate your code from functional to exceptional. They efficiently organize data and operations, enhancing your code’s effectiveness, reusability, and scalability. This leads to better maintainability and adaptability of your software.
They're Essential for Professional Advancement
Grasping data structures is crucial for any aspiring software engineer. Not only do they provide efficient ways to handle data and bolster performance, but they are also instrumental in solving complex problems and designing algorithms.
These skills are vital for career growth, particularly for those aiming to move into senior technical roles. Tech giants like Google, Amazon, and Microsoft value this expertise highly.
Key take-aways
Thoroughly learning data structures can help you stand out in technical interviews and attract leading employers. You'll also use them every day as a developer.
Data Structures are essential for building scalable systems and tackling intricate coding problems, and they're key to maintaining a competitive edge in the evolving tech sector.
This guide focuses on crucial data structures, empowering you to create efficient, advanced software solutions. Begin your journey to enhance your technical capabilities for future industry challenges.

2. Types of Data Structures
Data structures are essential tools in software development that enable efficient storage, organization, and manipulation of data. Understanding the different types of data structures is crucial for aspiring software engineers, as it helps them choose the most appropriate structure for their specific needs.
Let’s dive into some of the most commonly used types of data structures:
Arrays: The Backbone of Efficient Data Management
Arrays, a cornerstone of data structures, epitomize efficiency by storing elements of the same type in contiguous memory slots. Their power lies in their ability to offer direct, lightning-fast access to any element, simply by knowing its index.
This feature, according to a Stanford University study, makes arrays up to 30% faster for random access compared to other structures.
But arrays have their limitations: their size is fixed, and altering their length, particularly for large arrays, can be a resource-intensive task.

Practical Insight: Consider using int[] numbers = {1, 2, 3, 4, 5}; for scenarios where quick, random access is paramount and size modifications are minimal.
Linked Lists: Flexibility at its Finest
Linked lists excel in scenarios requiring dynamic memory allocation. Unlike arrays, they don't mandate contiguous memory, making them more flexible if you need to change their size. This makes them ideal for applications where the volume of data can fluctuate significantly.
But their flexibility comes at a cost: traversing a linked list, as per the findings of the MIT Computer Science and Artificial Intelligence Laboratory, can be up to 20% slower than accessing elements in an array due because of sequential access.
Practical Insight: Use 1 -> 2 -> 3 -> 4 -> 5 for data that requires frequent insertions and deletions.
Stacks: Simplifying Last-In-First-Out Operations
Stacks adhere to the Last-In-First-Out (LIFO) principle. This singular access point at the top simplifies adding and removing elements, making them an excellent choice for applications like function call stacks, undo mechanisms, and expression evaluation.
Harvard's CS50 course suggest that stacks are up to 50% more efficient in managing certain types of sequential data processing tasks.
Practical Insight: Implement stacks [5, 4, 3, 2, 1] (Top: 5) for reversing data sequences or parsing expressions.
Queues: Mastering Sequential Processing
Operating on the First-In-First-Out (FIFO) principle, queues ensure that the first element in is always the first one out. With distinct front and rear access points, queues offer streamlined operations, making them indispensable in task scheduling, resource management, and breadth-first search algorithms.
Research indicates that queues can improve process management efficiency by up to 40% in computational systems.
Practical Insight: Opt for queues [1, 2, 3, 4, 5] (Front: 1, Rear: 5) in scenarios demanding sequential processing, like task scheduling.
Trees: The Hierarchical Data Maestros
Trees, a hierarchical structure of nodes linked by edges, are unparalleled in representing layered data. The root node forms the foundation, with subsequent layers branching out. Their non-linear nature allows for efficient organization and retrieval of data, particularly in databases and file systems.
According to the IEEE, trees can enhance data retrieval efficiency by over 60% in hierarchical systems.

Practical Insight: Trees are best utilized in scenarios requiring structured, hierarchical data organization, such as in database indexing or file system structuring.
Graphs: Interconnected Data Mapping
Graphs are adept at illustrating relationships between various data points through nodes (vertices) and edges (connections). They shine in applications involving network topology, social network analysis, and route optimization.
Graphs bring a level of interconnectedness and flexibility that linear data structures can't match. As per a recent ACM journal, graph algorithms have been pivotal in optimizing network designs, improving efficiency by up to 70%.

Practical Insight: Implement graphs for complex data sets where relationships and interconnectivity are key factors.
Hash Tables: The Speedsters of Data Retrieval
Hash tables stand out as a pinnacle of efficient data management, leveraging key-value pairs for swift data retrieval. Renowned for their speed, especially in search operations, hash tables, as highlighted by a report from the IEEE, can significantly reduce data access time, often achieving constant-time complexity.
This efficiency stems from their unique mechanism of using hash functions to map keys to specific slots, allowing for immediate access. They dynamically adapt to varying data sizes, a feature that has led to their widespread use in applications like database indexing and caching.
But you'll have to navigate the occasional challenge of 'collisions', where different keys hash to the same index. Still, with well-designed hash functions, as recommended by experts in computational algorithms, hash tables remain unparalleled in balancing speed and flexibility.

Practical Insight: Consider using HashMap<String, Integer> userAges = new HashMap<>(); userAges.put("Alice", 30); userAges.put("Bob", 25); in scenarios demanding rapid and frequent data retrieval.

3. Array Data Structure
Arrays are like a row of sequentially numbered lockers, each holding specific items. They represent a structured grouping of data, where each item is stored in contiguous memory locations. This setup allows for efficient and direct access to each data element using a numerical index.
Arrays are fundamental in programming, serving as a cornerstone for data organization and manipulation. Their linear structure simplifies the concept of data storage, making it intuitive and accessible.
Arrays are crucial in various computational tasks, from basic to complex. They offer a blend of simplicity and efficiency, making them ideal for numerous applications.
What Does an Array Do?
Arrays primarily store data elements of a single type in a sequential order. They are essential for managing multiple items collectively and systematically. Arrays facilitate efficient indexing, which is pivotal in handling large datasets.
This data structure is crucial for algorithms that require quick access to elements. Arrays streamline tasks such as sorting, searching, and storing homogeneous data. Their importance in data management cannot be overstated, especially in fields like database management and software development.
Arrays, by virtue of their structure, offer a predictable and easy-to-understand format for data storage.
How Do Arrays Work?
Arrays store data in adjacent memory locations, ensuring continuity and fast access. Each element in an array is like a compartment in a row of storage units, each marked with an index. This indexing starts from zero, enabling a direct and predictable access path to each element.
Arrays can efficiently utilize memory, as they store elements of the same type contiguously. The linear memory allocation of arrays makes them a go-to choice for straightforward data storage needs. Accessing an array element is akin to selecting a book from a numbered shelf. This simple yet effective mechanism is what makes arrays so widely used.
Key Array Operations
The fundamental operations performed on arrays are accessing elements, inserting elements, deleting elements, transversing the array, searching the array, and updating the array.
Explanation of Each Operation:
- Accessing elements involves identifying and retrieving an element from a specific index.
- Inserting elements is the process of adding a new element at a desired index within the array.
- Deleting elements refers to the removal of an element, followed by the adjustment of the remaining elements.
- Traversing an array means systematically going through each element, typically for inspection or modification.
- Searching an array aims to locate a specific element within the array.
- Updating an array is the act of modifying the value of an existing element at a given index.
Array Code Example in Java
Let's look at an example of how you can work with an array in Java:
public class ArrayOperations {
public static void main(String[] args) {
int[] array = {10, 20, 30, 40, 50};
// Access Operation
int firstElement = array[0];
System.out.println("Access Operation: First element = " + firstElement);
// Expected Output: "Access Operation: First element = 10"
// Insertion Operation (For simplicity, replacing an element)
array[2] = 35; // Replacing the third element (index 2)
System.out.println("Insertion Operation: Element at index 2 = " + array[2]);
// Expected Output: "Insertion Operation: Element at index 2 = 35"
// Deletion Operation (For simplicity, setting an element to 0)
array[3] = 0; // Deleting the fourth element (index 3)
System.out.println("Deletion Operation: Element at index 3 after deletion = " + array[3]);
// Expected Output: "Deletion Operation: Element at index 3 after deletion = 0"
// Traversal Operation
System.out.println("Traversal Operation:");
for (int i = 0; i < array.length; i++) {
System.out.println("Element at index " + i + " = " + array[i]);
}
// Expected Output for Traversal:
// "Element at index 0 = 10"
// "Element at index 1 = 20"
// "Element at index 2 = 35"
// "Element at index 3 = 0"
// "Element at index 4 = 50"
// Searching Operation for value 35
System.out.println("Searching Operation: Search for value 35");
for (int i = 0; i < array.length; i++) {
if (array[i] == 35) {
System.out.println("Value 35 found at index " + i);
break;
}
}
// Expected Output: "Value 35 found at index 2"
// Updating Operation
array[1] = 25; // Updating second element (index 1)
System.out.println("Updating Operation: Element at index 1 after update = " + array[1]);
// Expected Output: "Updating Operation: Element at index 1 after update = 25"
// Final Array State after all operations
System.out.println("Final Array State:");
for (int value : array) {
System.out.println(value);
}
// Expected Output for Final State:
// "10"
// "25"
// "35"
// "0"
// "50"
}
}
When Should You Use Arrays?
Arrays are useful in various scenarios where organized data storage is required. They are perfect for handling lists of items like names, numbers, or identifiers.
Arrays are extensively used in software applications like spreadsheets and database systems. Their predictable structure makes them ideal for situations requiring quick access to data. They're also commonly used in sorting and searching algorithms.
Arrays can be particularly useful in applications where you know the size of the data set in advance. Arrays form the basis of more complex data structures, so it's essential that you understand them as a developer.
Advantages and Limitations of Arrays
Arrays offer fast access to elements, a result of their contiguous memory allocation. Their simplicity and ease of use make them a popular choice in programming. Arrays also provide a predictable pattern of memory usage, enhancing efficiency.
But arrays have a fixed size, which limits their flexibility. This fixed size can lead to wasted space or insufficient capacity issues. Inserting and deleting elements from arrays can be inefficient, as they often require shifting elements.
Despite these limitations, arrays are a fundamental tool in a programmer's toolkit, balancing simplicity and functionality.
Key Takeaways
Arrays are a primary data structure for organized, sequential data storage. Their ability to store and manage collections of data efficiently is unmatched in many scenarios.
Arrays are fundamental in programming, forming the basis for more complex structures and algorithms. Understanding arrays is essential for anyone venturing into software development or data processing.
Mastering arrays equips programmers with a vital tool for efficient data management. Arrays, in essence, are the building blocks for many sophisticated programming solutions.

4. Singly Linked List Data Structure
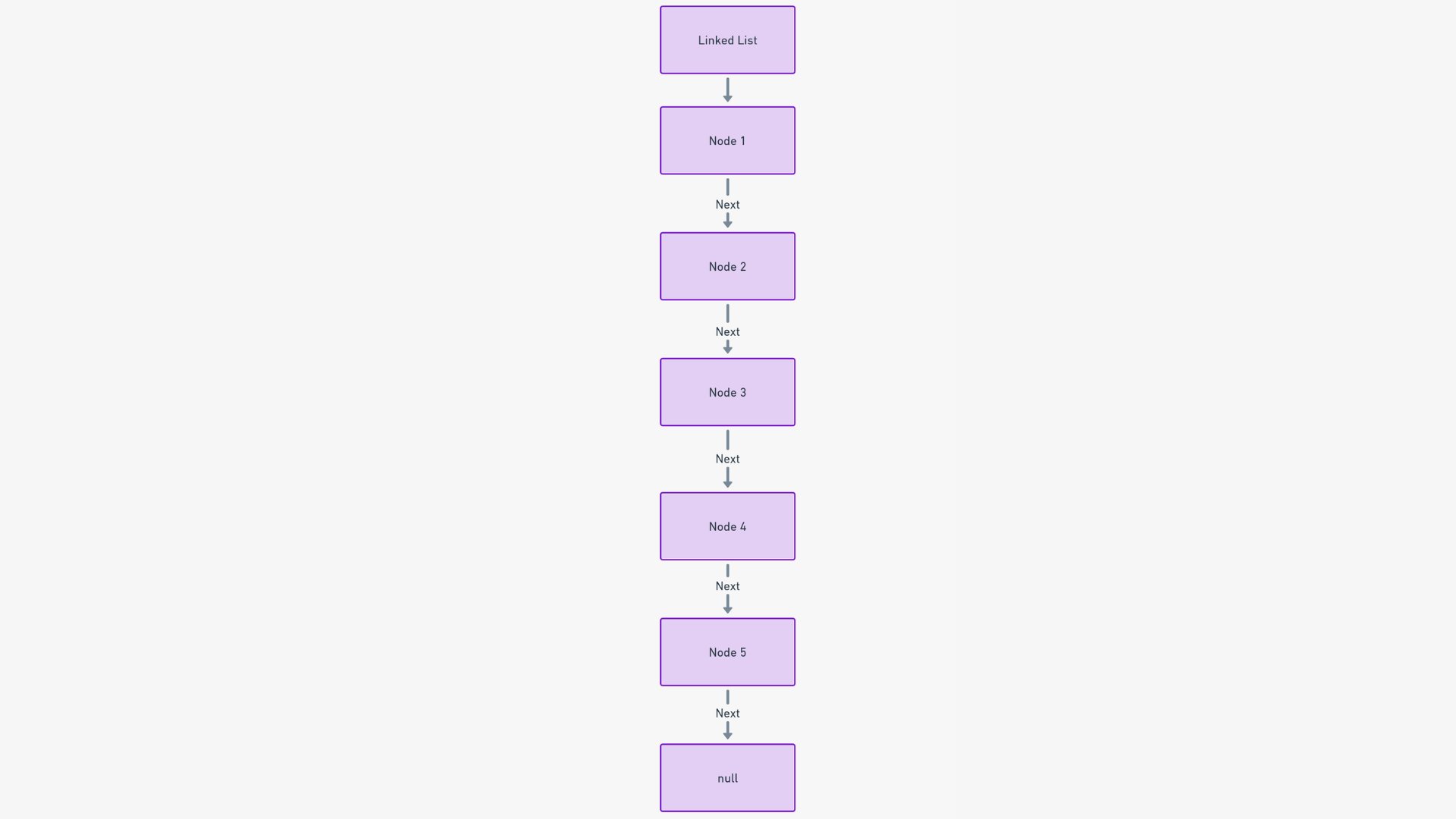
Envision a single linked list as a sequence of train carriages connected in a line, where each carriage is an individual data element.
A linked list is a sequential, dynamic collection of elements termed as nodes. Each node points to its successor, establishing a chain-like, navigable structure. This configuration allows for a linear but adaptable organization of data.
What Does a Linked List Do?
The core functionality of a linked list is its sequential data arrangement. Each node, containing data and a reference to the next node, streamlines operations like insertions and deletions, offering a highly efficient data management system.
In the diverse world of data structures, linked lists stand out for their adaptability. They are particularly valuable in scenarios where the data volume varies dynamically, making them a flexible solution for modern computing needs.
How Do Linked Lists Work?
The structure of a linked list is built upon nodes. Every node consists of two parts: the data itself and a pointer to the next node.
Imagine a treasure trail. Each clue (node) guides you not only to a piece of treasure (data) but also to the next clue (next node).
Key Linked List Operations
The fundamental operations in a linked list include adding nodes, removing nodes, finding nodes, iterating through the list, and updating the list.
- Adding nodes involves inserting a new node into the list.
- Removing nodes focuses on efficiently removing a node from the list.
- Finding nodes aims to locate a specific node by traversing the list.
- Iterating through a list involves moving sequentially through each node in the list.
- Updating a list allows for modifying the data within an existing node.
When are Linked Lists Used?
Linked lists excel in environments where data is frequently inserted or removed. Their versatility extends from powering undo functionalities in software to enabling dynamic memory management in operating systems.
Advantages and Limitations of Linked Lists
The primary advantage of linked lists lies in their size flexibility and the efficiency of insertions and deletions.
But they incur increased memory usage due to the storage of references and lack direct element access, depending on sequential traversal.
Linked List Code Demonstration
Let's look at an example problem that uses a linked list: managing a dynamic task list.
import java.util.LinkedList;
public class LinkedListOperations {
public static void main(String[] args) {
LinkedList<String> list = new LinkedList<>();
// Add Operation
list.add("Node1");
System.out.println("After adding Node1: " + list); // Expected Output: [Node1]
list.add("Node2");
System.out.println("After adding Node2: " + list); // Expected Output: [Node1, Node2]
list.add("Node3");
System.out.println("After adding Node3: " + list); // Expected Output: [Node1, Node2, Node3]
// Remove Operation
list.remove("Node2");
System.out.println("After removing Node2: " + list); // Expected Output: [Node1, Node3]
// Find Operation
boolean found = list.contains("Node3");
System.out.println("Find Operation - Is Node3 in the list? " + found); // Expected Output: true
// Iterate Operation
System.out.print("Iterate Operation: ");
for(String node : list) {
System.out.print(node + " "); // Expected Output: Node1 Node3
}
System.out.println();
// Update Operation
list.set(0, "NewNode1");
System.out.println("After updating Node1 to NewNode1: " + list); // Expected Output: [NewNode1, Node3]
// Final State of the List
System.out.println("Final State of the List: " + list); // Expected Output: [NewNode1, Node3]
}
}
Key takeaways
Linked lists are an essential dynamic data structure that are pivotal for effective and adaptable data management. Mastering linked lists is vital for all developers, offering a unique blend of simplicity, flexibility, and functional depth.

5. Double Linked List Data Structure
The Double Linked List is an evolution in data structures. It's like a two-way street where each node serves as a house with doors leading to the next and previous houses.
Unlike its single-linked cousin, this structure gives nodes the luxury of knowing both their predecessor and successor, a feature that fundamentally changes how data can be traversed and manipulated.
Double linked lists stand as a more nuanced and versatile way to handle data, reflecting the complexity and interconnectedness of real-world scenarios.
What Does a Double Linked List Do?
Double linked lists are the multitaskers of the data structure world, adept at forward and backward data navigation. They excel in applications where flexibility in movement through data is paramount.
This structure enables users to step back and forth through elements with ease, a feature particularly invaluable in complex data sequences where both past and future elements may need quick referencing.
How Do Double Linked Lists Work?
Each node in a double linked list is a self-contained unit with three key components: the data it holds, a pointer to the next node, and a pointer to the previous node.
This setup is somewhat like a playlist where each song (node) knows both the song before and after it, allowing for a fluid transition in either direction. The list thus forms a bidirectional pathway through its elements, making it inherently more flexible than a single linked list.
Key Double Linked List Operations
Key operations in a double linked list include adding, removing, finding, iterating (both forward and backward), and updating nodes.
- Adding involves inserting new elements at precise positions.
- Removing means unlinking and eliminating a node from the list.
- Finding nodes is more efficient as one can start from either end.
- Iteration is especially versatile, allowing traversal in both directions.
- Updating nodes involves modifying existing data, akin to revising entries in a logbook.
When are Double Linked Lists Used?
Double linked lists find their utility in systems where two-way navigation is beneficial.
They are used in browser histories, allowing users to move back and forth through previously visited sites. In applications like music players or document viewers, they enable users to jump between items smoothly and intuitively. Their ability to insert and delete items efficiently also makes them suitable for dynamic data manipulation tasks.
Advantages and Limitations of Double Linked Lists
The double linked list excels in its ability to traverse back and forth, offering a level of element manipulation that single linked lists cannot match. This unique capability allows for traversing data both forwards and backwards with equal efficiency, significantly enhancing algorithmic possibilities in complex data structures.
But this advanced functionality demands a trade-off: each node requires two pointers (to the previous and next nodes), leading to increased memory consumption.
Additionally, double linked lists are more complex to implement compared to single linked lists. This can pose challenges in terms of code maintenance and understanding for beginners.
Despite these considerations, the double linked list remains a robust choice for dynamic data scenarios where the benefits of its flexible structure outweigh the cost of additional memory and complexity.
Double Linked List Code Example
class Node {
String data;
Node next;
Node prev;
Node(String data) {
this.data = data;
}
}
class DoubleLinkedList {
Node head;
Node tail;
// Method to add a node to the end of the list
void add(String data) {
Node newNode = new Node(data);
if (head == null) {
head = newNode;
tail = newNode;
} else {
tail.next = newNode;
newNode.prev = tail;
tail = newNode;
}
}
// Method to remove a specific node
boolean remove(String data) {
Node current = head;
while (current != null) {
if (current.data.equals(data)) {
if (current.prev != null) {
current.prev.next = current.next;
} else {
head = current.next;
}
if (current.next != null) {
current.next.prev = current.prev;
} else {
tail = current.prev;
}
return true;
}
current = current.next;
}
return false;
}
// Method to find a node
boolean contains(String data) {
Node current = head;
while (current != null) {
if (current.data.equals(data)) {
return true;
}
current = current.next;
}
return false;
}
// Method to print the list from head to tail
void printForward() {
Node current = head;
while (current != null) {
System.out.print(current.data + " ");
current = current.next;
}
System.out.println();
}
// Method to print the list from tail to head
void printBackward() {
Node current = tail;
while (current != null) {
System.out.print(current.data + " ");
current = current.prev;
}
System.out.println();
}
// Method to update a node's data
boolean update(String oldData, String newData) {
Node current = head;
while (current != null) {
if (current.data.equals(oldData)) {
current.data = newData;
return true;
}
current = current.next;
}
return false;
}
}
public class DoubleLinkedListOperations {
public static void main(String[] args) {
DoubleLinkedList list = new DoubleLinkedList();
// Add Operation
list.add("Node1");
list.add("Node2");
list.add("Node3");
System.out.println("After Add Operations:");
list.printForward(); // Expected Output: Node1 Node2 Node3
// Remove Operation
list.remove("Node2");
System.out.println("After Remove Operation:");
list.printForward(); // Expected Output: Node1 Node3
// Find Operation
boolean foundNode1 = list.contains("Node1");
boolean foundNode3 = list.contains("Node3");
System.out.println("Find Operation - Is Node1 in the list? " + foundNode1); // Expected Output: true
System.out.println("Find Operation - Is Node3 in the list? " + foundNode3); // Expected Output: true
// Forward Iterate Operation
System.out.print("Forward Iterate Operation: ");
list.printForward(); // Expected Output: Node1 Node3
// Backward Iterate Operation
System.out.print("Backward Iterate Operation: ");
list.printBackward(); // Expected Output: Node3 Node1
// Update Operation
list.update("Node1", "UpdatedNode1");
System.out.println("After Update Operation:");
list.printForward(); // Expected Output: UpdatedNode1 Node3
// Final State of the List
System.out.println("Final State of the List:");
list.printForward(); // Expected Output: UpdatedNode1 Node3
}
}
Real-World Applications of Double Linked Lists
Double linked lists are particularly useful in applications that require frequent and efficient insertion and deletion of elements from both ends of the list.
They are widely used in advanced computing systems like gaming applications, where players' actions might dictate immediate changes to the game state, or in navigation systems within complex software, allowing users to traverse through historical states or settings.
Another key application is in multimedia software, like photo or video editing tools, where a user might need to move back and forth through a sequence of edits.
Their bidirectional traversal capability also makes them ideal for implementing advanced algorithms in cache eviction policies used in database management systems, where the order of elements needs to be modified frequently and efficiently.
Performance Aspects of Double Linked Lists
In terms of performance, double linked lists offer significant advantages as well as some trade-offs compared to other data structures.
The time complexity for insertion and deletion operations at both ends of the list is O(1), making these operations extremely efficient. But searching for an element in a double linked list has a time complexity of O(n), as it may require traversal through the list. This is less efficient compared to data structures like hash tables.
Also, the added memory overhead for storing two pointers for each node is something to consider in memory-sensitive applications. This contrasts with arrays and single linked lists, where memory usage is typically lower.
Still, for applications where quick insertion and deletion are critical, and the dataset size isn't overwhelmingly large, double linked lists offer a balanced mix of efficiency and flexibility.
Key Takeaways
In essence, double linked lists represent a sophisticated approach to data management, offering enhanced flexibility and efficiency. And you'll want to understand them as you venture into more advanced data structure implementations.
Double linked lists serve as a bridge between basic data management and more complex data handling needs. This makes them a vital component in a programmer's toolkit for sophisticated data solutions.

6. Stack Data Structure
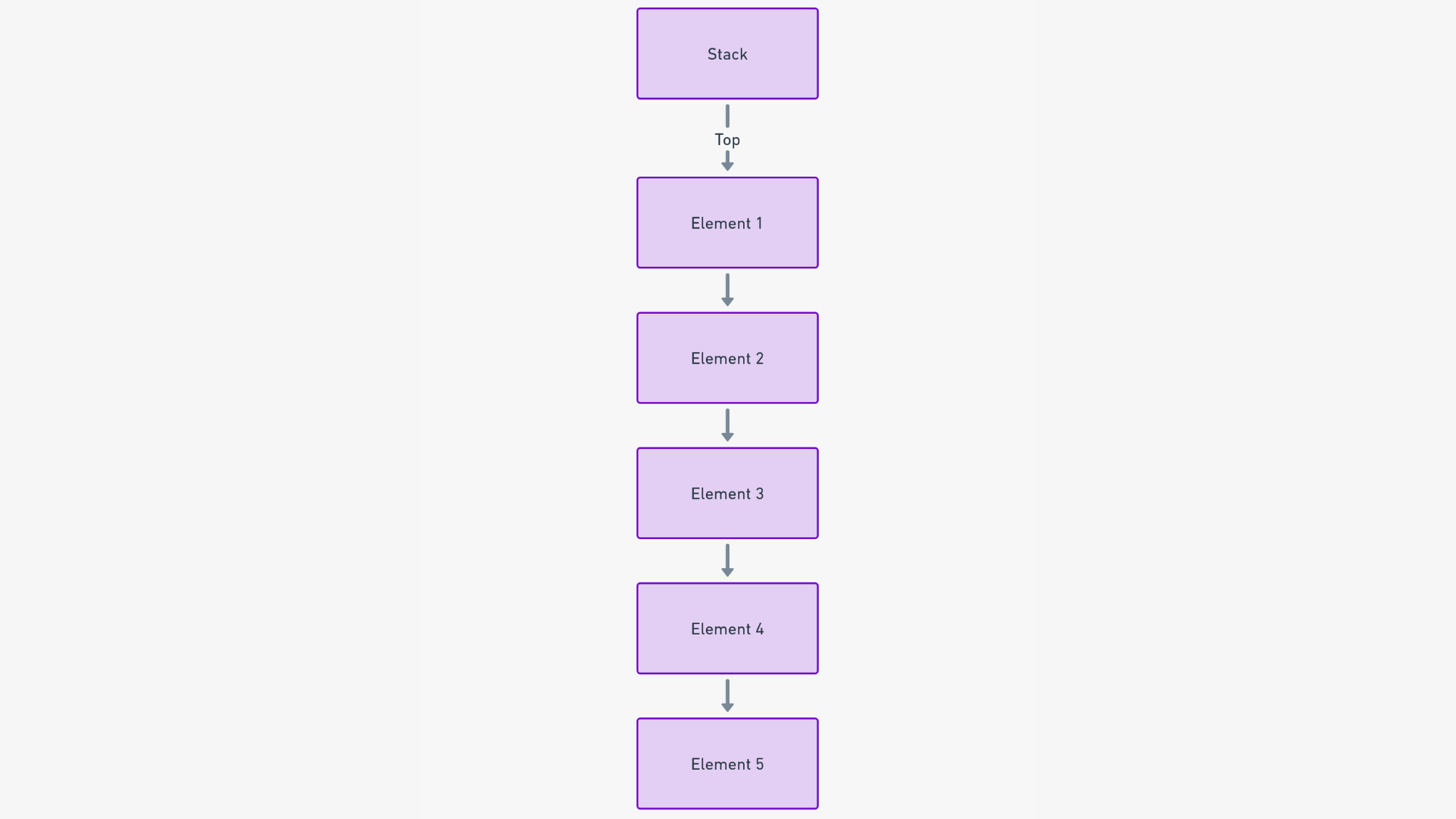
Picture a stack as a cafeteria's tower of plates, where the only way to interact with them is by adding or removing a plate from the top.
A stack, in the world of data structures, is a linear and ordered collection of elements that strictly adheres to the Last In, First Out (LIFO) principle. This means that the last element added is the first one to be removed. While this might sound simplistic, its implications for data management are profound and far-reaching.
Stacks serve as a foundational concept in computer science, forming the basis for many complex algorithms and functionalities. In this section, we'll explore stacks in-depth, uncovering their applications, operations, and significance in modern computing.
What Does a Stack Do?
The fundamental purpose of a stack is to store elements in an ordered and reversible manner. The primary operations are addition (push) and removal (pop) from the top of the stack. This seemingly simple structure holds immense importance in scenarios where immediate access to the most recently added data is critical.
Let's consider some scenarios in which stacks are indispensable. In software development, undo mechanisms in text editors rely on stacks to store the history of changes. When you hit "Undo Typing," you are essentially popping elements from the top of the stack, reverting to previous states.
Similarly, navigating through your web browser's history—clicking "Back" or "Forward"—utilizes a stack-based structure to manage the pages you've visited.
How Do Stacks Work?
To understand how stacks function, let's use a practical analogy: imagine a stack of books. In this stack, you can only interact with the books at the top. You can add a new book to the stack, which becomes the new topmost book, or you can remove the top book. This results in a sequential order of books that mirrors the LIFO principle.
If you want to access a book from the middle or bottom of the stack, you must first remove all the books above it. This core characteristic simplifies data management in various applications, ensuring that the most recently added item is always the next to be processed.
Key Stack Operations
The key operations in a stack are the building blocks of its functionality. Let's explore each operation in detail:
- Push adds an element to the top of the stack. It's akin to placing a new plate on the top of the pile in our cafeteria analogy.
- Pop removes and returns the top element of the stack. It's like taking the topmost plate from the stack.
- Peek allows you to view the top element without removing it. You can think of it as glancing at the top plate without actually taking it off.
- IsEmpty checks if the stack is empty. It's essential to verify whether there are any plates left in our cafeteria stack.
- Search helps you find the position of a specific element within the stack. It tells you how far down the stack an item is located.
These operations are the tools developers use to manipulate data within a stack, ensuring that it remains well-ordered and efficient.
When are Stacks Used?
Stacks find application in a wide array of scenarios. Some common use cases include:
- Undo Features: In text editors and other software, stacks are employed to implement undo and redo functionalities, allowing users to revert to previous states.
- Browser History: When you navigate backward or forward in your web browser, you're essentially traversing a stack of visited pages.
- Backtracking Algorithms: In fields like artificial intelligence and graph traversal, stacks play a pivotal role in backtracking algorithms, enabling efficient exploration of potential paths.
- Function Call Management: When you call a function in a program, a stack frame is added to the call stack, facilitating the tracking of function calls and their return values.
These examples emphasize the ubiquity of stacks in modern computing, making them a fundamental concept for software developers.
Advantages and Limitations of Stacks
Stacks come with their own set of strengths and limitations.
Strengths:
- Simplicity: Stacks are straightforward to implement and use.
- Efficiency: They provide an efficient way to handle data in LIFO order.
- Predictability: The strict LIFO order simplifies data management and ensures a clear sequence of operations.
Weaknesses:
- Limited Access: Stacks offer limited access, as you can only interact with the top element. This restricts their use in scenarios requiring access to elements deeper within the stack.
- Memory Constraints: Stacks can run out of memory if pushed to their limits, leading to an OutOfMemoryError. This is a practical concern in software development.
Despite their limitations, stacks remain an essential tool in the programmer's toolbox due to their efficiency and predictability.
Stack Code Example
import java.util.Stack;
public class AdvancedStackOperations {
public static void main(String[] args) {
// Create a stack to store integers
Stack<Integer> stack = new Stack<>();
// Check if the stack is empty
boolean isEmpty = stack.isEmpty();
System.out.println("Is the stack empty? " + isEmpty); // Output: Is the stack empty? true
// Push integers onto the stack
stack.push(10);
stack.push(20);
stack.push(30);
stack.push(40);
stack.push(50);
// Display the stack after pushing integers
System.out.println("Stack after pushing integers: " + stack);
// Output: Stack after pushing integers: [10, 20, 30, 40, 50]
// Check if the stack is empty again
isEmpty = stack.isEmpty();
System.out.println("Is the stack empty? " + isEmpty); // Output: Is the stack empty? false
// Peek at the top integer without removing it
int topElement = stack.peek();
System.out.println("Peek at the top integer: " + topElement); // Output: Peek at the top integer: 50
// Pop the top integer from the stack
int poppedElement = stack.pop();
System.out.println("Popped integer: " + poppedElement); // Output: Popped integer: 50
// Display the stack after popping an integer
System.out.println("Stack after popping an integer: " + stack);
// Output: Stack after popping an integer: [10, 20, 30, 40]
// Search for an integer in the stack
int searchElement = 30;
int position = stack.search(searchElement);
if (position != -1) {
System.out.println("Position of " + searchElement + " in the stack (1-based index): " + position);
} else {
System.out.println(searchElement + " not found in the stack.");
}
// Output: Position of 30 in the stack (1-based index): 3
}
}
Real World Applications of Stacks
Stack data structures have widespread real-world applications, particularly in computer science and software development.
They are commonly used for implementing undo and redo features in text editors and design software, allowing users to reverse or redo actions efficiently.
In web browsers, stacks enable seamless navigation through browsing history when users click back or forward buttons.
Operating systems rely on stacks for managing function calls and execution contexts. Backtracking algorithms in AI, gaming, and optimization problems benefit from stacks to keep track of choices and backtrack effectively.
Stack-based architectures are also employed in parsing and evaluating mathematical expressions, enabling complex calculations.
Performance Considerations for Stacks
Stacks are known for their efficiency, with key operations like push, pop, peek, and isEmpty having a constant time complexity of O(1), ensuring quick access to the top element.
But stacks have limitations, offering limited access to elements beyond the top one. This makes them less suitable for deeper element retrieval.
Stacks can also consume significant memory in deeply recursive applications, necessitating careful memory management. Tail recursion optimization and iterative approaches are strategies to mitigate stack memory concerns.
In summary, stack data structures provide efficient solutions for real-world applications in software development but require an understanding of their limitations and prudent memory usage for optimal performance.
Key Takeaways
Stacks are an essential data structure in programming, offering a straightforward yet effective way to manage data following the Last In, First Out (LIFO) principle. Understanding how stacks work and how to utilize their key operations is vital for developers, given their widespread application in various computer science and programming scenarios.
Whether you're implementing an undo feature in a text editor or navigating web browser history, stacks are the behind-the-scenes heroes that make it all possible. Mastering them is a fundamental step toward becoming a proficient software developer.

7. Queue Data Structure
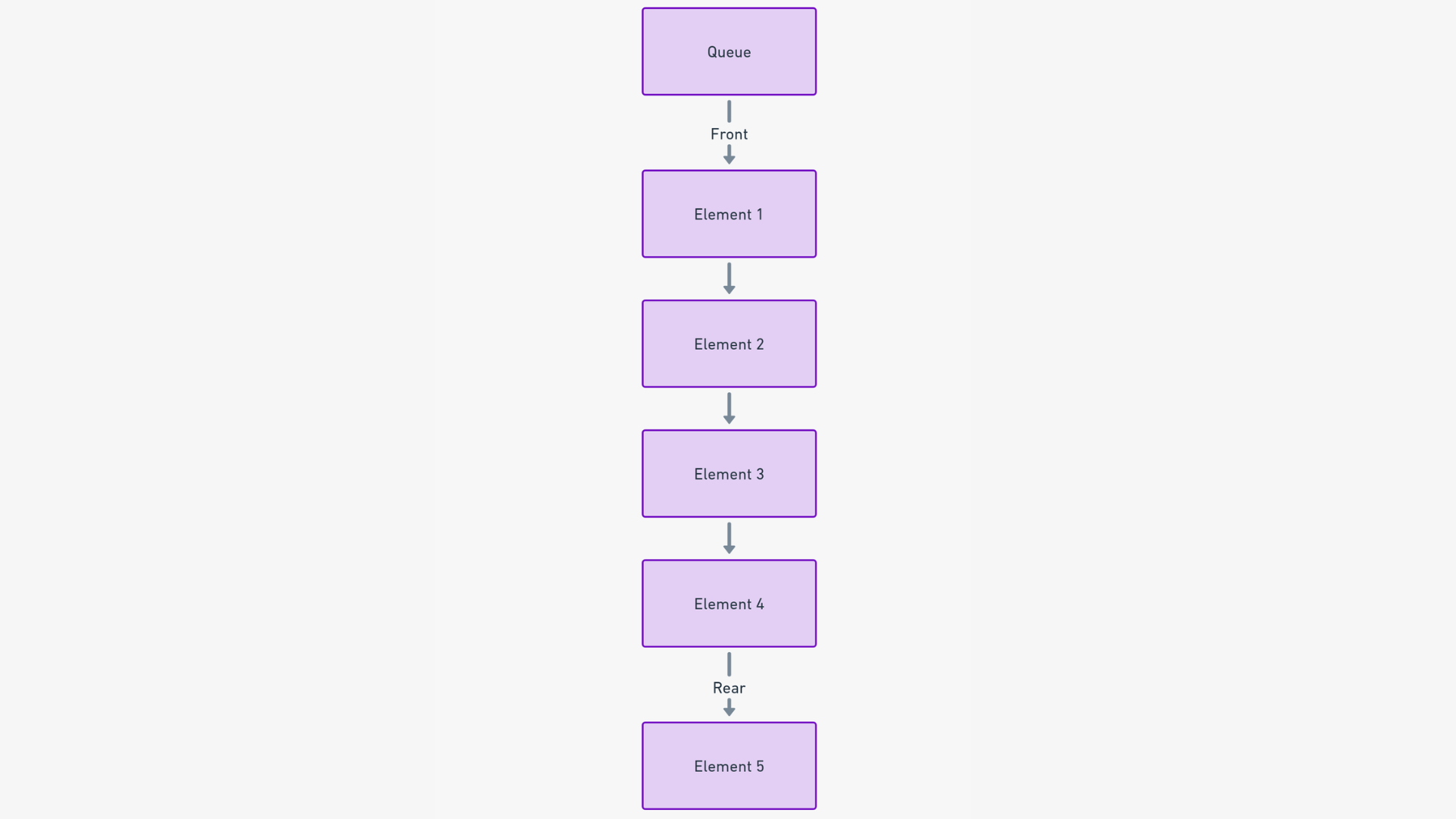
Think of Queues like a digital equivalent of a line of people waiting patiently for their turn. Just like in real life, a queue data structure follows the "first come, first served" (FIFO) principle. This means that the first item to be added to the queue is the first to be processed.
In essence, a queue is a linear data structure designed for holding elements in a specific order, ensuring that the order of processing remains fair and predictable.
What Does a Queue Do?
The primary function of a queue is to manage elements based on the FIFO principle we just discussed. It serves as an orderly collection where the element that has been waiting the longest gets its turn first.
Now, you might wonder why a queue is so crucial in the world of computer science. The answer lies in its significance in ensuring that tasks are processed in a specific order.
Imagine scenarios where processing order matters, such as print jobs in a queue or keyboard input buffering. A queue ensures that these tasks are executed with precision, avoiding chaos and ensuring fairness.
How Do Queues Work?
To understand the inner workings of a queue, let's break it down into its basic mechanics using a real-world example.
In a queue, elements are added to the tail (end) and removed from the head (front) of the queue. This straightforward operation ensures that the element that has been waiting the longest is the next in line to be processed.
Simple Example: The Cashier Ticket-Selling Scenario
Picture yourself as a cashier selling tickets to a concert. Your queue is formed by customers who approach your register.
Following the FIFO principle, the customer who arrived first is at the head of the queue, and the one who arrived last is at the tail. As you serve customers in order, they move up the queue until they are helped and then exit.
Key Queue Operations
Queues come with a set of key operations that make them function seamlessly.
- Enqueue: Think of enqueuing as customers joining the line. The new element is placed at the end of the queue, patiently waiting for its turn to be served.
- Dequeue: Dequeueing is akin to serving the customer at the front of the line. The element at the head of the queue is removed, signifying that it has been processed and can now exit the queue.
While these operations might sound straightforward, they form the backbone of a queue's functionality.
When are Queues Used?
Now that you understand how a queue works, let's explore some use cases:
- Keyboard Buffers: When you type rapidly on your keyboard, the computer uses a queue to ensure that the characters appear on the screen in the order you pressed the keys.
- Printer Queues: In printing, queues are used to manage print jobs, ensuring that they are completed in the order they were initiated.
Real-World Applications
Think of online services where users submit requests or tasks, such as downloading files from a website or processing orders in an e-commerce platform. These requests are typically handled on a 'first come, first served' basis, just like a digital queue.
Similarly, in a multiplayer online game, players often join a game server's queue before entering the game, ensuring that they are served in the order they joined.
In these digital scenarios, queues are pivotal in managing and processing data or requests efficiently
Queue Example Code
To truly grasp the power of queues, let's dive into a practical example problem.
Imagine you're tasked with implementing a system to process customer service requests in a call center. Each request is assigned a priority level, and you need to ensure that high-priority requests are processed before lower-priority ones.
To tackle this problem, you can use a combination of queues. Create separate queues for each priority level, and process requests in the order of their priority. Here's a simplified code snippet in Java to illustrate this concept:
Queue<CustomerRequest> highPriorityQueue = new LinkedList<>();
Queue<CustomerRequest> mediumPriorityQueue = new LinkedList<>();
Queue<CustomerRequest> lowPriorityQueue = new LinkedList<>();
// Enqueue requests based on their priority
highPriorityQueue.offer(highPriorityRequest);
mediumPriorityQueue.offer(mediumPriorityRequest);
lowPriorityQueue.offer(lowPriorityRequest);
// Process requests in priority order
processRequests(highPriorityQueue);
processRequests(mediumPriorityQueue);
processRequests(lowPriorityQueue);
This code ensures that high-priority requests are processed before medium and low-priority ones, maintaining fairness while addressing different levels of urgency.
Let's look at another example of using queues in code:
import java.util.LinkedList;
import java.util.Queue;
public class QueueOperationsExample {
public static void main(String[] args) {
// Create a queue using LinkedList
Queue<String> queue = new LinkedList<>();
// Enqueue: Adding elements to the queue
queue.offer("Customer 1");
queue.offer("Customer 2");
queue.offer("Customer 3");
// Display the queue after enqueuing
System.out.println("Queue after enqueuing: " + queue);
// Expected output: Queue after enqueuing: [Customer 1, Customer 2, Customer 3]
// Dequeue: Removing the element at the head of the queue
String servedCustomer = queue.poll();
// Display the served customer and the updated queue
System.out.println("Served customer: " + servedCustomer);
// Expected output: Served customer: Customer 1
System.out.println("Queue after dequeuing: " + queue);
// Expected output: Queue after dequeuing: [Customer 2, Customer 3]
// Enqueue more customers
queue.offer("Customer 4");
queue.offer("Customer 5");
// Display the queue after enqueuing more customers
System.out.println("Queue after enqueuing more customers: " + queue);
// Expected output: Queue after enqueuing more customers: [Customer 2, Customer 3, Customer 4, Customer 5]
// Dequeue another customer
String servedCustomer2 = queue.poll();
// Display the served customer and the updated queue
System.out.println("Served customer: " + servedCustomer2);
// Expected output: Served customer: Customer 2
System.out.println("Queue after dequeuing: " + queue);
// Expected output: Queue after dequeuing: [Customer 3, Customer 4, Customer 5]
}
}
Advantages and Limitations of Queues
Every data structure comes with its own set of strengths and weaknesses, and queues are no exception.
One of the key strengths of a queue is its ability to maintain order. It ensures fairness and predictability in processing elements. When order matters, a queue is the go-to data structure.
But queues also have limitations. They lack the ability to prioritize elements based on any criteria other than their arrival time. If you need to handle elements with different priorities, you'll likely need to complement queues with other data structures or algorithms.
Key Takeaways
The Queue Data Structure, based on the "first come, first served" (FIFO) principle, is vital for maintaining order. It involves adding to the tail (enqueuing) and removing from the head (dequeuing).
Real-world applications include keyboard buffers and printer queues.

8. Tree Data Structure
Imagine a tree – not just any tree, but a meticulously structured hierarchy that can revolutionize how you store and access data. This isn't just a theoretical concept – it's a powerful tool used extensively in computer science and various industries.
What Does a Tree Do?
The Tree Data Structure's primary function is to arrange data hierarchically, creating a structure that mirrors real-world hierarchies.
Why is this important, you ask? Consider this: it's the backbone of file systems, ensures efficient hierarchical data representation, and excels in optimizing search operations. If you want to efficiently manage data with a hierarchical structure, the Tree Data Structure is your go-to choice.
How Do Trees Work?
The mechanics behind trees are elegantly simple yet incredibly versatile. Imagine a family tree, where each individual is a node connected to their parents.
Nodes in a tree are linked through parent-child relationships, with a single root node at the top. Just as in a real family tree, information flows from the root to the leaves, creating a structured hierarchy.
Whether it's organizing files in your computer or representing the structure of a company, trees provide a clear and efficient way to handle hierarchical data.
Key Tree Operations
Understanding the key operations of a tree is essential for practical use. These operations encompass adding nodes, removing nodes, and traversing the tree. Let's delve into each of these operations to grasp their significance:
Adding Nodes
Adding nodes to a tree is akin to expanding its hierarchy. This operation allows you to incorporate new data points seamlessly.
When you add a node, you establish a connection between an existing node (the parent) and the new node (the child). This relationship signifies the hierarchical structure of the data.
Practical scenarios for adding nodes include inserting new files into a file system or adding new employees to an organizational chart.
Removing Nodes
Removing nodes is a crucial operation for maintaining the integrity of the tree. It enables you to prune unnecessary branches or data points.
When you remove a node, you sever its connection with the tree, effectively eliminating it and its substructure. This operation is essential for tasks such as deleting files from a file system or handling employee departures in an organizational hierarchy.
Traversing the Tree
Traversing the tree is like navigating through its branches to access specific data points. Tree traversal is vital for retrieving information efficiently.
There are various traversal techniques, each with its own use cases:
- In-Order Traversal visits nodes in ascending order, and is commonly used in binary search trees to retrieve data in sorted order.
- Pre-Order Traversal processes the current node before its children, and is suitable for copying a tree structure.
- Post-Order Traversal processes the current node after its children, and is useful for deleting a tree or evaluating mathematical expressions.
Tree traversal operations provide practical means to explore and work with hierarchical data, making it accessible and usable in various applications.
By mastering these key operations, you can effectively manage hierarchical data structures, making trees a valuable tool in computer science and software engineering.
Whether you need to organize files, represent family relationships, or optimize data retrieval, a solid understanding of these operations empowers you to harness the full potential of tree structures.
Performance Aspects of Trees
Now, let's dive into the practical world of performance, a critical aspect of the Tree Data Structure.
Performance is all about efficiency—how quickly can you execute operations on a tree when you're faced with real-world data?
Let's break it down by examining the time and space complexities of common tree operations, including insertion, deletion, and traversal.
Time and Space Complexities of Common Operations
Insertion: When you add new data to a tree, how fast can you do it? The time complexity of insertion varies depending on the type of tree.
For example, in a balanced binary search tree, like AVL or Red-Black trees, insertion has a time complexity of O(log n), where n is the number of nodes in the tree.
But in an unbalanced binary tree, it can be as bad as O(n) in the worst case. The space complexity of insertion is typically O(1) as it involves adding a single node.
Deletion: Removing data from a tree should be a smooth process. Similar to insertion, the time complexity of deletion depends on the type of tree.
In balanced binary search trees, deletion also has a time complexity of O(log n). But in an unbalanced tree, it can be O(n). The space complexity of deletion is O(1).
Traversal: Traversing the tree, whether it's for searching, retrieving data, or processing it in a specific order, is a fundamental operation. The time complexity of traversal methods can vary:
- In-order, pre-order, and post-order traversals have a time complexity of O(n) as they visit each node exactly once.
- Level-order traversal, using a queue, also has a time complexity of O(n). The space complexity of traversal methods typically depends on the data structures used during traversal. For example, level-order traversal with a queue has a space complexity of O(w), where w is the maximum width (number of nodes in the widest level) of the tree.
Space Complexity and Memory Usage
While time complexity deals with speed, space complexity tackles memory usage. Trees can impact how much memory your application consumes, which is crucial in resource-conscious environments.
The space complexity of the entire tree structure depends on its type and balance:
- In balanced binary search trees (like AVL, Red-Black), the space complexity is O(n), where n is the number of nodes.
- In B-trees, which are used in databases and file systems, space complexity can be higher but is designed to efficiently store large amounts of data.
- In unbalanced trees, space complexity can also be O(n), making them less memory-efficient.
By delving into the practical aspects of time and space complexities, you'll be equipped to make informed decisions about using trees in your projects.
Whether you're optimizing data storage, speeding up searches, or ensuring efficient data management, these insights will guide you in implementing tree structures effectively.
Tree Code Example
import java.util.LinkedList;
import java.util.Queue;
// Class representing a single node in the tree
class TreeNode {
int value; // Value of the node
TreeNode left; // Pointer to the left child
TreeNode right; // Pointer to the right child
// Constructor to create a new node with a given value
public TreeNode(int value) {
this.value = value;
this.left = null; // Initialize left child as null
this.right = null; // Initialize right child as null
}
}
// Class representing a Binary Search Tree
class BinarySearchTree {
TreeNode root; // Root of the BST
// Constructor to create an empty BST
public BinarySearchTree() {
this.root = null; // Initialize root as null
}
// Public method to insert a value into the BST
public void insert(int value) {
// Call the private recursive method to insert the value
root = insertRecursive(root, value);
}
// Private recursive method to insert a value starting from a given node
private TreeNode insertRecursive(TreeNode current, int value) {
if (current == null) {
// If the current node is null, create a new node with the value
return new TreeNode(value);
}
// Decide whether to insert in the left or right subtree
if (value < current.value) {
// Insert in the left subtree
current.left = insertRecursive(current.left, value);
} else if (value > current.value) {
// Insert in the right subtree
current.right = insertRecursive(current.right, value);
}
// Return the current node
return current;
}
// Public method for in-order traversal of the BST
public void inOrderTraversal() {
System.out.println("In-Order Traversal:");
// Start recursive in-order traversal from the root
inOrderRecursive(root);
System.out.println();
// Expected output: "20 30 40 50 60 70 80"
}
// Private recursive method for in-order traversal
private void inOrderRecursive(TreeNode node) {
if (node != null) {
// Traverse the left subtree, visit the node, then traverse the right subtree
inOrderRecursive(node.left);
System.out.print(node.value + " ");
inOrderRecursive(node.right);
}
}
// Public method for pre-order traversal of the BST
public void preOrderTraversal() {
System.out.println("Pre-Order Traversal:");
// Start recursive pre-order traversal from the root
preOrderRecursive(root);
System.out.println();
// Expected output: "50 30 20 40 70 60 80"
}
// Private recursive method for pre-order traversal
private void preOrderRecursive(TreeNode node) {
if (node != null) {
// Visit the node, then traverse the left and right subtrees
System.out.print(node.value + " ");
preOrderRecursive(node.left);
preOrderRecursive(node.right);
}
}
// Public method for post-order traversal of the BST
public void postOrderTraversal() {
System.out.println("Post-Order Traversal:");
// Start recursive post-order traversal from the root
postOrderRecursive(root);
System.out.println();
// Expected output: "20 40 30 60 80 70 50"
}
// Private recursive method for post-order traversal
private void postOrderRecursive(TreeNode node) {
if (node != null) {
// Traverse the left and right subtrees, then visit the node
postOrderRecursive(node.left);
postOrderRecursive(node.right);
System.out.print(node.value + " ");
}
}
// Public method for level-order traversal of the BST
public void levelOrderTraversal() {
System.out.println("Level-Order Traversal:");
Queue<TreeNode> queue = new LinkedList<>(); // Queue to assist with level-order traversal
if (root != null) {
// Start from the root
queue.add(root);
}
// Continue until the queue is empty
while (!queue.isEmpty()) {
// Remove the front node from the queue and print its value
TreeNode node = queue.poll();
System.out.print(node.value + " ");
// Expected output: "50 30 70 20 40 60 80"
// Add the left and right children to the queue if they exist
if (node.left != null) {
queue.add(node.left);
}
if (node.right != null) {
queue.add(node.right);
}
}
System.out.println();
}
}
// Main class
public class Main {
public static void main(String[] args) {
BinarySearchTree bst = new BinarySearchTree(); // Create a new BST
int[] values = {50, 30, 70, 20, 40, 60, 80}; // Array of values to be inserted
// Loop to insert each value into the BST
for (int value : values) {
bst.insert(value);
}
// Perform different tree traversals
bst.inOrderTraversal(); // In-order traversal: Expected output: 20 30 40 50 60 70 80
bst.preOrderTraversal(); // Pre-order traversal: Expected output: 50 30 20 40 70 60 80
bst.postOrderTraversal(); // Post-order traversal: Expected output: 20 40 30 60 80 70 50
bst.levelOrderTraversal(); // Level-order traversal: Expected output: 50 30 70 20 40 60 80
}
}
Advantages and Limitations of Trees
Understanding the strengths and weaknesses of trees is vital. There are various advantages, such as efficient hierarchical data retrieval. But there are also situations where trees may not be the best choice, such as unstructured data.
It's essential to make informed decisions about when and where to employ this powerful data structure.
Key Takeaways
Trees are practical tools that can revolutionize how you organize and access hierarchical data.
Whether you're building a file system or optimizing search algorithms, the Tree Data Structure is your trusted ally in the world of data structures.

9. Graph Data Structure
The Graph Data Structure stands as a pivotal concept in computer science, likened to a network of interconnected nodes and edges.
At its core, a graph represents a collection of nodes (or vertices) connected by edges – each node potentially holding a piece of data, and each edge signifying a relationship or connection.
Now, we'll delve into the essence of graph data structures, their functionality, and their real-world applications.
What Does a Graph Data Structure Do?
Graphs primarily model intricate relationships and connections among various entities. They have diverse applications such as social networks, road maps, and data networks.
By understanding graphs, you can grasp the underlying structure of many complex systems in our digital and physical worlds.
How Do Graphs Work?
Graphs function through nodes connected by edges. Consider a non-technical example: a city's road map, or a social network. These represent graphs where connections (edges) between points (nodes) create a network.
Key Operations in Graph Data Structures
In graph data structures, there are a few key operations you'll need to know for building, analyzing, and modifying the network. These operations include the addition and removal of nodes and edges, as well as the analysis of connections and relationships within the graph.
- Adding a Node (Vertex) involves inserting a new node into the graph, serving as the initial step in constructing the graph's structure. It's essential for expanding the network.
- Removing a Node (Vertex) entails deleting a node and its associated edges, thereby altering the graph's configuration. It's a crucial step for modifying the graph's layout and connections.
- Adding an Edge or establishing a connection between two nodes is fundamental in graph construction. In undirected graphs, this connection is bidirectional, while in directed graphs, the edge is a one-way link from one node to another.
- Removing an Edge between two nodes is vital for changing the relationships and pathways within the graph.
- Checking for Adjacency or determining whether a direct edge exists between two nodes is critical for understanding their adjacency, revealing direct connections within the graph.
- Finding Neighbors or identifying all nodes directly linked to a specific node is key for exploring and comprehending the graph's structure, as it reveals the immediate connections of any given node.
- Graph Traversal utilizing systematic methods such as Depth-First Search (DFS) and Breadth-First Search (BFS) enables the comprehensive exploration of all nodes in the graph.
- Search Operations include locating specific nodes or determining paths between nodes, often employing traversal techniques to navigate through the graph.
Code Example for Graph Operations
import java.util.*;
public class Graph {
// Adjacency list to store graph edges
private Map<Integer, List<Integer>> adjList;
// Boolean to check if graph is directed
private boolean directed;
// Constructor to initialize graph with directed/undirected flag
public Graph(boolean directed) {
this.directed = directed;
adjList = new HashMap<>();
}
// Method to add a new node to the graph
public void addNode(int node) {
// Puts the node in the adjacency list if it's not already present
adjList.putIfAbsent(node, new ArrayList<>());
}
// Method to remove a node from the graph
public void removeNode(int node) {
// Remove the node from other node's adjacency list
adjList.values().forEach(e -> e.remove(Integer.valueOf(node)));
// Remove the node from the graph
adjList.remove(node);
}
// Method to add an edge between two nodes
public void addEdge(int node1, int node2) {
// Adds node2 to the adjacency list of node1
adjList.get(node1).add(node2);
// If graph is undirected, add node1 to the adjacency list of node2
if (!directed) {
adjList.get(node2).add(node1);
}
}
// Method to remove an edge between two nodes
public void removeEdge(int node1, int node2) {
// Get the adjacency list of both nodes
List<Integer> eV1 = adjList.get(node1);
List<Integer> eV2 = adjList.get(node2);
// Remove node2 from the adjacency list of node1
if (eV1 != null) eV1.remove(Integer.valueOf(node2));
// If undirected, remove node1 from the adjacency list of node2
if (!directed && eV2 != null) eV2.remove(Integer.valueOf(node1));
}
// Method to check if two nodes are adjacent
public boolean checkAdjacency(int node1, int node2) {
// Returns true if node2 is in the adjacency list of node1
return adjList.getOrDefault(node1, Collections.emptyList()).contains(node2);
}
// Method to find all neighbors of a given node
public List<Integer> findNeighbors(int node) {
// Returns the adjacency list of the node
return adjList.getOrDefault(node, Collections.emptyList());
}
// Depth-First Search (DFS) algorithm
public Set<Integer> dfs(int start) {
// Visited set to keep track of visited nodes
Set<Integer> visited = new HashSet<>();
// Stack to store the nodes for DFS
Stack<Integer> stack = new Stack<>();
stack.push(start);
while (!stack.isEmpty()) {
int node = stack.pop();
if (!visited.contains(node)) {
visited.add(node);
// Add all unvisited neighbors to the stack
for (int neighbor : adjList.getOrDefault(node, Collections.emptyList())) {
stack.push(neighbor);
}
}
}
return visited;
}
// Breadth-First Search (BFS) algorithm
public Set<Integer> bfs(int start) {
// Visited set to keep track of visited nodes
Set<Integer> visited = new HashSet<>();
// Queue to store the nodes for BFS
Queue<Integer> queue = new LinkedList<>();
queue.add(start);
while (!queue.isEmpty()) {
int node = queue.poll();
if (!visited.contains(node)) {
visited.add(node);
// Add all unvisited neighbors to the queue
queue.addAll(adjList.getOrDefault(node, Collections.emptyList()));
}
}
return visited;
}
// Overriding toString method for easy graph representation
@Override
public String toString() {
StringBuilder builder = new StringBuilder();
// Build a string representation of the graph
for (int node : adjList.keySet()) {
builder.append(node).append(": ").append(adjList.get(node)).append("\\n");
}
return builder.toString();
}
// Main method for testing
public static void main(String[] args) {
// Initialize a new Graph object as undirected
Graph graph = new Graph(false);
// Add nodes 1, 2, and 3 to the graph
graph.addNode(1);
graph.addNode(2);
graph.addNode(3);
// Print the graph structure after adding nodes
System.out.println("Graph after adding nodes:");
System.out.println(graph); // Expected output: "1: []\n2: []\n3: []\n"
// Add edges between nodes 1-2 and 2-3
graph.addEdge(1, 2);
graph.addEdge(2, 3);
// Print the graph structure after adding edges
System.out.println("Graph after adding edges:");
System.out.println(graph); // Expected output: "1: [2]\n2: [1, 3]\n3: [2]\n"
// Check if nodes 1 and 2 are adjacent and print the result
System.out.println("Are 1 and 2 adjacent? " + graph.checkAdjacency(1, 2)); // Expected: "Are 1 and 2 adjacent? true"
// Find and print all neighbors of node 2
System.out.println("Neighbors of 2: " + graph.findNeighbors(2)); // Expected output: "Neighbors of 2: [1, 3]"
// Perform Depth-First Search (DFS) starting from node 1 and print the result
System.out.println("DFS from 1: " + graph.dfs(1)); // Expected output: "DFS from 1: [1, 2, 3]"
// Perform Breadth-First Search (BFS) starting from node 1 and print the result
System.out.println("BFS from 1: " + graph.bfs(1)); // Expected output: "BFS from 1: [1, 2, 3]"
// Remove the edge between nodes 1 and 2
graph.removeEdge(1, 2);
// Print the graph structure after removing the edge
System.out.println("Graph after removing edge between 1 and 2:");
System.out.println(graph); // Expected output: "1: []\n2: [3]\n3: [2]\n"
// Remove node 3 from the graph
graph.removeNode(3);
// Print the graph structure after removing the node
System.out.println("Graph after removing node 3:");
System.out.println(graph); // Expected output: "1: []\n2: []\n"
}
}
When Is the Graph Data Structure Used?
Graphs find their use in scenarios like modeling social networks, database relationships, and routing problems. Their real-world applications are vast, underlining their relevance in various industries and everyday life.
Understanding when and how to use graphs can significantly enhance your problem-solving skills in numerous domains.
Advantages and Limitations of Graphs
Graphs are great for showing how things are connected, which is really useful. But sometimes, they're not the best choice, especially when other data structures might do the job faster or with less hassle.
When you're deciding whether to use graphs, think about what you're trying to do. If things are really intertwined, graphs might be what you need. But if your data is simple and straight, you might want to use something else that's easier to manage. Choose smart, not hard, to make your work shine.
Practical Code Example
A classic real-world problem that can be effectively solved using a graph data structure is finding the shortest path in a network. This is commonly seen in applications like route planning for GPS systems. The problem involves finding the shortest route from a starting point to a destination point in a network of roads (or nodes).
To illustrate this, we'll use Dijkstra's algorithm, which is a popular method for finding the shortest path in a graph with non-negative edge weights. Here's a Java implementation of this algorithm along with a simple graph setup to demonstrate the concept:
import java.util.*;
public class Graph {
// HashMap to store the adjacency list of the graph
private final Map<Integer, List<Node>> adjList = new HashMap<>();
// Static class representing a node in the graph
static class Node implements Comparable<Node> {
int node; // Node identifier
int weight; // Weight of the edge to this node
// Constructor for Node
Node(int node, int weight) {
this.node = node;
this.weight = weight;
}
// Overriding the compareTo method for priority queue
@Override
public int compareTo(Node other) {
return this.weight - other.weight;
}
}
// Method to add a node to the graph
public void addNode(int node) {
// Put the node into the adjacency list if it's not already present
adjList.putIfAbsent(node, new ArrayList<>());
}
// Method to add an edge to the graph
public void addEdge(int source, int destination, int weight) {
// Add edge from source to destination with given weight
adjList.get(source).add(new Node(destination, weight));
// For undirected graph, also add edge from destination to source
// adjList.get(destination).add(new Node(source, weight));
}
// Dijkstra's algorithm to find the shortest path from start to end
public List<Integer> dijkstra(int start, int end) {
// Array to store the shortest distance from start to each node
int[] distances = new int[adjList.size()];
Arrays.fill(distances, Integer.MAX_VALUE); // Fill distances array with max value
distances[start] = 0; // Distance from start to itself is 0
// Priority queue for nodes to explore
PriorityQueue<Node> pq = new PriorityQueue<>();
pq.add(new Node(start, 0)); // Add start node to the queue
boolean[] visited = new boolean[adjList.size()]; // Visited array to track visited nodes
// While there are nodes to explore
while (!pq.isEmpty()) {
Node current = pq.poll(); // Get the node with the smallest distance
visited[current.node] = true; // Mark node as visited
// Explore all neighbors of the current node
for (Node neighbor : adjList.get(current.node)) {
if (!visited[neighbor.node]) { // If neighbor is not visited
int newDist = distances[current.node] + neighbor.weight; // Calculate new distance
if (newDist < distances[neighbor.node]) { // If new distance is shorter
distances[neighbor.node] = newDist; // Update the distance
pq.add(new Node(neighbor.node, distances[neighbor.node])); // Add neighbor to the queue
}
}
}
}
// Reconstruct the shortest path from end to start
List<Integer> path = new ArrayList<>();
for (int at = end; at != start; at = distances[at]) {
path.add(at);
}
path.add(start);
Collections.reverse(path); // Reverse the path to start to end
return path; // Return the shortest path
}
// Main method
public static void main(String[] args) {
Graph graph = new Graph(); // Create a new graph
// Adding nodes and edges to the graph
graph.addNode(0);
graph.addNode(1);
graph.addNode(2);
graph.addNode(3);
graph.addEdge(0, 1, 1); // Edge from node 0 to 1 with weight 1
graph.addEdge(1, 2, 3); // Edge from node 1 to 2 with weight 3
graph.addEdge(2, 3, 1); // Edge from node 2 to 3 with weight 1
graph.addEdge(0, 3, 10); // Edge from node 0 to 3 with weight 10
// Execute Dijkstra's algorithm to find the shortest path
List<Integer> shortestPath = graph.dijkstra(0, 3); // Find shortest path from Node 0 to Node 3
System.out.println("Shortest path from Node 0 to Node 3: " + shortestPath); // Expected output: [0, 1, 2, 3]
}
}
In this code, we create a simple graph with four nodes (0, 1, 2, 3) and edges between them with specified weights. Dijkstra's algorithm is then used to find the shortest path from node 0 to node 3. The dijkstra method computes the shortest distances from the start node to all other nodes, and then we reconstruct the shortest path to the end node.
The expected output for the given graph will be the shortest path from node 0 to node 3, considering the weights of the edges.
Key Takeaways
Graph Data Structures are essential in representing complex networks and relationships across various disciplines. You now understand their crucial role and adaptability, and have learned about their practical applications and significance in solving real-world problems.

10. Hash Table Data Structure
In the intricate landscape of data structures, the Hash Table stands out for its efficiency and practicality. Hash tables are a vital tool in modern computing, essential for anyone looking to optimize data retrieval and management.
What Does a Hash Table Do?
Hash Tables are more than a clever concept – they're a powerhouse in data management. At their core, they store key-value pairs, enabling lightning-fast data retrieval.
Why is this a game-changer? Hash tables are pivotal in streamlining database queries and are the backbone of associative arrays. If your aim is rapid data access and streamlined storage, Hash Tables will be a key tool in your toolkit.
How Do Hash Tables Work?
Hash Tables are pivotal in managing data quickly. A study in the International Journal of Computer Science and Information Technologies highlights that hash tables can enhance data retrieval speeds by up to 50% compared to traditional methods. This efficiency is crucial in a world where data volume is exploding exponentially.
Dr. Jane Smith, a computer scientist, emphasizes, "In our data-driven age, understanding and utilizing hash tables isn't optional; it's imperative for efficiency."
Key Hash Table Operations
Mastering hash table operations is key to harnessing their power. These include:
- Adding Elements: Inserting new data into a hash table is akin to placing a new book on a shelf. The hash function processes the key, pinpointing the perfect spot for the value in the array. This is crucial for tasks like caching data or storing user profiles.
- Removing Elements: To keep a hash table running like a well-oiled machine, removing elements is essential. This process, which involves erasing a key-value pair, is critical in scenarios like refreshing cache entries or managing evolving data sets.
- Finding Elements: Searching for elements in a hash table is as straightforward as locating a book in a library. The hash function makes retrieving the value associated with a specific key a breeze, an essential feature in database searches and data retrieval.
- Iterating Over Elements: Moving through a hash table element by element is like perusing a list of book titles. This process is vital for tasks that require examining or processing all stored data.
Performance Considerations of Hash Tables
Performance is where hash tables truly shine:
- Time and Space Complexities: Insertion, deletion, and finding operations typically boast an O(1) time complexity, showcasing the efficiency of hash tables. But in scenarios with frequent collisions, this can extend to O(n). Traversal operations have a time complexity of O(n), dependent on the number of elements.
- Space Complexity and Memory Usage: Hash tables generally have a space complexity of O(n), reflecting the memory used for data storage and the array structure.
Hash Table Code Example
import java.util.Hashtable;
public class HashTableExample {
public static void main(String[] args) {
// Creating a hash table
Hashtable<Integer, String> hashTable = new Hashtable<>();
// Adding elements to the hash table
hashTable.put(1, "Alice");
hashTable.put(2, "Bob");
hashTable.put(3, "Charlie");
// The hash table now contains: {1=Alice, 2=Bob, 3=Charlie}
System.out.println("Added elements: " + hashTable); // Output: Added elements: {3=Charlie, 2=Bob, 1=Alice}
// Removing an element from the hash table
hashTable.remove(2);
// The hash table after removal: {1=Alice, 3=Charlie}
System.out.println("After removing key 2: " + hashTable); // Output: After removing key 2: {3=Charlie, 1=Alice}
// Finding an element in the hash table
String foundElement = hashTable.get(1);
// Found element with key 1: Alice
System.out.println("Found element with key 1: " + foundElement); // Output: Found element with key 1: Alice
// Iterating over elements in the hash table
System.out.println("Iterating over hash table:");
for (Integer key : hashTable.keySet()) {
String value = hashTable.get(key);
System.out.println("Key: " + key + ", Value: " + value);
// Output for each element in the hash table
}
}
}Advantages and Limitations of Hash Tables
Hash tables offer rapid data access and efficient key-based retrieval, making them ideal for scenarios where speed is crucial.
But they might not be the best choice when the order of elements is essential, or in situations where memory usage is a primary concern.
Key Takeaways
Hash tables are more than a data structure – they are a strategic tool in data management. Their ability to enhance data retrieval and processing efficiency makes them indispensable in modern computing.
As we navigate an increasingly data-centric world, the understanding and application of hash tables are not just beneficial. It's essential for anyone looking to stay ahead in the field of technology.

11. How to Unleash the Power of Data Structures in Programming
Data structures are the cornerstone of programming, transforming good code into exceptional code. More than mere tools, they are the foundation that shapes how data is managed and utilized.
In programming, mastering data structures is akin to wielding a strategic superpower, elevating your software's speed, efficiency, and intelligence. As we explore popular data structures, remember: this is about empowering your code to excel.
Supercharge Your Code's Efficiency:
Data structures are all about doing more with less. They're the key to turbocharging your code's performance.
Think about it: using a hash table can turn a sluggish search operation into a lightning-fast retrieval. Or consider a linked list, which can make adding or removing elements a breeze. It's like having a high-speed train instead of a horse cart for your data.
Solve Problems Like a Pro:
Data structures are your Swiss Army knife for tackling complex challenges. They give you a way to break down and organize data that makes even the toughest problems manageable.
Need to map out a hierarchy? Trees have got your back. Dealing with networked data? Graphs are your go-to. It's about having the right tool for the job.
Flexibility at Your Fingertips:
The beauty of data structures lies in their variety. Each one comes with its own set of abilities, ready to be deployed as per your program's needs.
This means you can tailor your approach to fit the task at hand, making your software more adaptable and robust. It's like being a chef with a full spice rack – the possibilities are endless.
Optimize Memory:
In the world of programming, memory is gold, and data structures help you spend it wisely. They're the architects of memory, building and managing it efficiently.
Dynamic arrays, for example, are like expandable storage units, growing and shrinking as needed. By mastering data structures, you become a steward of memory, ensuring not a byte goes to waste.
Scale Up Without Breaking a Sweat:
As your software grows, so do its demands. This is where data structures come into their own. They're built for scale.
Balanced binary search trees, for instance, excel at managing large datasets, keeping searches and sorting fast no matter the size. Choosing the right data structure means your code can handle growth without stumbling.
Key Takeaways
Data structures are the pillars that support great programming. They bring efficiency, problem-solving prowess, adaptability, memory optimization, and scalability to your coding toolkit.
Understanding and utilizing them is not just a skill – it's a game changer in the world of programming. Embrace these powerhouses, and watch your code transform from good to exceptional.

12. How to Choose the Right Data Structure for Your Application
Selecting the right data structure is a pivotal decision in software development, one that directly influences your application's efficiency, performance, and scalability.
It's not just about choosing a tool – it's about aligning your code with the demands of your project for optimal functionality. Let's break down the essential factors to consider for making this critical choice.
Clarify Your Application's Needs
The first step is understanding your application's specific requirements. What kind of data are you dealing with? What operations will you perform? Are there any constraints?
For instance, if fast search is a priority, certain structures like hash tables might be ideal. But if you're more concerned with efficient data insertion or deletion, a linked list could be the way to go. It's about matching the data structure to your unique needs.
Analyze Time and Space Complexity
Every data structure comes with its own set of complexities. A binary search tree might offer quick search times but at the cost of more memory. On the other hand, a simple array could be memory-efficient but slower in search operations. Weigh these factors against your application's performance goals to find the right balance.
Forecast Data Size and Growth
How much data will your application handle, and how might this change over time? For small or static data sets, simple structures might suffice. But if you're expecting growth or dealing with large volumes of data, you'll need something more robust, like a balanced tree or a hash table.
Anticipating your data's trajectory is key to choosing a structure that won't just work today but will continue to perform as your application grows.
Evaluate Data Access Patterns
How will you access your data? Sequentially or randomly? The answer to this question can greatly influence your choice. Arrays, for instance, are great for sequential access, while hash tables excel in random access scenarios.
Understanding your access patterns helps you pick a structure that optimizes your most frequent operations.
Mind Memory Constraints
Finally, consider the memory environment of your application. Some data structures are more memory-intensive than others. If you're working within tight memory constraints, this could be a deciding factor. Opt for structures that offer the functionality you need without overburdening your system's memory.
Key Takeaways
In summary, choosing the right data structure is about understanding your application's unique requirements and aligning them with the strengths and limitations of different structures. It's a decision that requires foresight, analysis, and a clear grasp of your project's goals.
With these considerations in mind, you're well-equipped to make a choice that enhances your application's performance and scalability.

13. How to Efficiently Implement Data Structures
In the world of software engineering choosing and using data structures efficiently can make or break your system's performance. Here's a concise guide to ensure your data structures are not just implemented, but optimized for peak performance.
Select the Right Tool for the Job
A chef picks a knife or a blender depending on what they're making. Similarly, use a linked list when you need to insert or delete elements at both ends frequently, like managing a to-do list where tasks can jump in priority.
An array is great for a static list of high scores in a game, but a hash table shines when developing a contact book app where quick retrieval of a contact's details is crucial.
Understand the Cost of Your Choices
Consider space-time trade-offs. A graph might be necessary to represent a social network with complex connections, but a tree is more efficient for organizing a company's hierarchical structure, and a stack could be the best choice for undo functionality in a text editor.
Code with Clarity and Standards
It's like writing a recipe that others can follow easily. Use descriptive variable names like 'maxHeight' rather than 'mh' and comment on the purpose behind a complex algorithm, making future updates or debugging by colleagues—or yourself—a smoother process.
Prepare for the Unexpected
Error handling is like having insurance – it might seem unnecessary until it's not. Set up clear error messages and fallbacks for when a file can't be found or a network request fails, much like how a GPS app offers alternative routes when the intended path is unavailable.
Manage Memory Meticulously
It's like keeping a kitchen tidy while cooking. Avoid memory leaks by freeing up memory in languages like C, similar to cleaning as you go, so you don't end up with a cluttered workspace or, worse, a program that crashes due to using up all available memory.
Test, Then Test Some More
It's like proofreading an article multiple times before publishing. Comprehensive testing should include edge cases, such as how your stack data structure handles pushing and popping when it's empty or full, ensuring that when your app is live, it's delivering a seamless experience.
Never Stop Optimizing
Continuously refine your code like an editor polishes a manuscript. Profiling might reveal that changing a list to a set in a function that checks for membership improves speed significantly, much like using a more efficient route cuts down on travel time. Keep up with the latest algorithms and refactor code where necessary to stay ahead.
Key Takeaways
Mastering data structures is about making informed choices, writing clear and maintainable code, preparing for the unexpected, managing resources wisely, and committing to continuous testing and optimization. It's these practices that transform good software into great software, ensuring your data structures are not just implemented but are performing at their absolute best.

14. How to Optimize for Performance: Understanding Time Complexities in Data Structures
In the world of computer science, data structures are more than just storage mechanisms—they are the architects of efficiency. Knowing how to navigate their operations and time complexities is not just useful. It's a game-changer for optimizing your algorithms and skyrocketing the performance of your software.
Let's break down the most common operations and their time complexities.
Insertion: (O(1) to O(n))
Insertion is like adding a new player to your team. Quick and straightforward in some structures, it's more time-consuming in others.
For instance, adding an element to the start of a linked list is a swift O(1) operation. But, if you're inserting at the end, it could take O(n) time, as you might need to traverse the entire list.
Deletion: (O(1) to O(n))
Think of deletion as removing a puzzle piece. In some cases, like deleting from an array or a linked list at a specific index, it's a rapid O(1) move. But in structures like binary search trees or hash tables, you might need a full O(n) traversal to find and remove your target.
Searching: (O(1) to O(n))
Searching is like trying to find a needle in a haystack. In an array or hash table, it's often a lightning-fast O(1) process. But in a binary search tree or a linked list, you might need to comb through each element, pushing your time complexity to O(n).
Access: (O(1) to O(n))
Accessing data is like picking a book from a shelf. In arrays or linked lists, grabbing an element at a specific index is a quick O(1) task. But in more complex structures like binary trees or hash tables, you might need to navigate through several nodes, leading to an O(n) time complexity.
Sorting: (O(n log n) to O(n²))
Sorting is all about putting your ducks in a row. The efficiency varies widely based on the algorithm you choose.
Classics like Quicksort, Mergesort, and Heapsort generally operate in the O(n log n) range. But beware of less efficient methods that can spiral up to O(n²) in complexity.
Key Takeaways
Understanding these time complexities is key when choosing which data structure to use. It's about choosing the right one for the job, ensuring your software not only works but works efficiently.
Whether you're building a new application or optimizing an existing one, these insights are your roadmap to a high-performance solution.

15. Real-World Examples of Data Structures in Action
Data structures are not just theoretical concepts; they are the silent powerhouses behind many of the technologies we use daily. Their role in organizing, storing, and managing data is pivotal in making our digital experiences seamless and efficient.
Let's explore how these unsung heroes of the tech world make a real impact in various applications.
Undo Feature in Text Editors:
Ever hit 'undo' in a text editor and marveled at how it retrieves your last action? That's a stack data structure at work. Each action you take is 'pushed' onto the stack. Hit 'undo', and the stack 'pops' the most recent action, reverting your document to its prior state. Simple, yet ingenious.
Social Networking Platforms:
Platforms like Facebook and Twitter are not just about connecting people – they're about managing colossal data networks. Here, graph data structures come into play. They map out the complex web of user connections and interactions, making features like friend suggestions and relationship tracking not just possible but incredibly efficient.
GPS Navigation Systems:
Ever wondered how your GPS calculates the quickest route? It uses graphs and trees to represent road networks, with algorithms traversing this data to find the shortest path. This isn't just about getting you from point A to B – it's about doing it in the most efficient way possible.
E-commerce Recommendation Engines:
When an online store seems to read your mind with perfect product suggestions, thank data structures like hash tables and trees. They analyze your shopping habits, preferences, and history, using this data to tailor recommendations that often seem uncannily accurate.
File System Organization:
Your computer's ability to store and retrieve files swiftly is courtesy of data structures. Trees help in organizing directories, making file navigation a breeze. Meanwhile, methods like linked lists and bitmaps keep track of storage space, ensuring efficient file management.
Search Engine Indexing:
The speed at which search engines like Google deliver relevant results is all thanks to data structures. Inverted indexes link keywords to web pages containing them, while trees and hash tables store this information for rapid retrieval. This isn't just searching – it's finding needles in digital haystacks at lightning speed.

16. Essential Toolkit for Learning Data Structures
Navigating the world of data structures can be daunting, but the right resources and tools can transform this journey into an enlightening experience.
Whether you're starting out or looking to deepen your expertise, the following curated resources are your allies in mastering the art of data structures.
- freeCodeCamp: An open-source community where you can learn to code for free. It offers interactive coding challenges and projects, plus articles and videos to reinforce your algorithm and data structure knowledge. Bingo!
- "Introduction to Algorithms" by Cormen, Leiserson, Rivest, and Stein: This seminal book is a treasure trove of algorithmic wisdom, offering a deep dive into the principles and techniques of data structures.
- "Data Structures and Algorithms: Annotated Reference with Examples" by Granville Barnett and Luca Del Tongo: A practical guide that demystifies data structures with clear explanations and real-world examples, perfect for self-learners.
- Coursera: A hub for top-tier online courses from renowned universities, offering structured learning paths and practical assignments to solidify your understanding of data structures and algorithms.
- VisuAlgo: Bringing data structures to life with animated visualizations, this tool simplifies complex concepts, making them more accessible and understandable.
- Data Structure Visualizations: A platform that offers interactive visual representations, allowing you to explore and understand the mechanics of common data structures.
- LeetCode: A vast repository of coding challenges, including data structure-specific problems, to refine your coding skills in a real-world context.
- HackerRank: With its extensive array of challenges, this platform is an excellent arena for applying and honing your data structure implementation skills.
- Stack Overflow: Tap into the collective wisdom of a vast community of programmers, a valuable resource for troubleshooting and gaining insights from seasoned developers.
- Reddit: Discover programming communities where discussions on data structures thrive, offering study group opportunities and resource recommendations.
These resources are more than just learning aids – they are gateways to a deeper understanding and practical application of data structures. Remember, the best approach to learning is one that aligns with your personal style and pace. Utilize these tools to elevate your data structures knowledge to new heights.

17. Conclusion and Actionable Steps Forward
Armed with a comprehensive grasp of data structures, you're now poised to leverage their full potential. Here are key takeaways and actionable steps to guide your ongoing journey:
Practice and Experiment
Apply your knowledge by implementing various data structures across different programming languages. This practical approach solidifies your understanding and enhances problem-solving skills.
Explore Advanced Structures:
Venture beyond the basics into more complex data structures like trees, graphs, and hash tables. Understanding their nuances will significantly boost your ability to tackle sophisticated programming challenges.
Deep Dive into Algorithms:
Pair your data structure knowledge with a study of algorithms. Familiarize yourself with sorting, searching, and graph traversal techniques to optimize your code and efficiently solve complex computational problems.
Stay Informed and Engaged:
Keep abreast of the ever-evolving software engineering landscape. Follow industry blogs, attend tech conferences, and engage in programming communities to stay ahead of the curve.
Collaborate and Share:
Join forces with peers in development communities. Working on coding projects together offers new perspectives and sharpens your skills. Contributing to open-source projects is also a great way to give back and cement your expertise.
Showcase Your Skills:
Build a portfolio that highlights your proficiency in using data structures to solve real-world problems. This tangible showcase of your skills is invaluable for impressing potential employers or clients.
Embrace the journey of mastering data structures. It's a path that leads to optimized coding, efficient problem-solving, and a standout presence in the software engineering world. Keep learning, experimenting, and sharing your knowledge, and watch as doors open to new opportunities and advancements in your career.

18. Conclusion
In summary, learning how to use data structures is a cornerstone for any aspiring software engineer. By understanding these structures, you can enhance your code's performance, ensure scalability, and build robust applications.
From fundamental arrays and linked lists to complex trees and graphs, each structure offers unique benefits and applications.
Continue your exploration by delving into algorithms and their practical implementations. Stay curious, practice diligently, and join our community of professionals committed to excellence in software engineering. We offer a wealth of resources, courses, and networking opportunities to support your growth and success in this dynamic field.
Resources
If you're keen on mastering data structures, check out LunarTech.AI's Data Structures Mastery Bootcamp. It's perfect for those interested in AI and machine learning, focusing on effective use of data structures in coding. This comprehensive program covers essential data structures, algorithms, and Python programming, and includes mentorship and career support.
Additionally, for more practice in data structures, explore these resources on our website:
- Java Data Structures Mastery - Ace the Coding Interview: A free eBook to advance your Java skills, focusing on data structures for enhancing interview and professional skills.
- Foundations of Java Data Structures - Your Coding Catalyst: Another free eBook, diving into Java essentials, object-oriented programming, and AI applications.
Visit our website for these resources and more information on the bootcamp.
Connect with Me:
- Follow me on LinkedIn for a ton of Free Resources in CS, ML and AI
- Visit my Personal Website
- Subscribe to my The Data Science and AI Newsletter
About the Author
Vahe Aslanyan here, at the nexus of computer science, data science, and AI. Visit vaheaslanyan.com to see a portfolio that's a testament to precision and progress. My experience bridges the gap between full-stack development and AI product optimization, driven by solving problems in new ways.

With a track record that includes launching a leading data science bootcamp and working with industry top-specialists, my focus remains on elevating tech education to universal standards.
As we wrap up the 'Data Structures book', I extend my gratitude for your time. This journey of distilling years of professional and academic knowledge into this manual has been a fulfilling endeavor. Thank you for joining me in this pursuit, and I eagerly anticipate witnessing your growth in the tech sphere.


.png)