Dynamic Programming is an approach where the main problem is divided into smaller sub-problems, but these sub-problems are not solved independently.
For a problem to be solved using dynamic programming, the sub-problems must be overlapping. This means that two or more sub-problems will evaluate to give the same result.
So, we use the memoization technique to recall the result of the already solved sub-problems for future use. We then use cache storage to store this result, which is used when a similar sub-problem is encountered in the future.
Now let's look at this topic in more depth.
What is memoization?
Memoization is the technique of memorizing the results of certain specific states, which can then be accessed to solve similar sub-problems. In other words, it is a specific form of caching.
This ensures that the results already computed are stored generally as a hashmap. This decreases the run time significantly, and also leads to less complicated code.
But we know that any benefit comes at the cost of something. So, when we use dynamic programming, the time complexity decreases while space complexity increases.
Different approaches in DP
In dynamic programming, we can either use a top-down approach or a bottom-up approach.
The top-down approach involves solving the problem in a straightforward manner and checking if we have already calculated the solution to the sub-problem.
This approach includes recursive calls (repeated calls of the same function). It builds up a call stack, which leads to memory costs. It is also vulnerable to stack overflow errors.
The bottom-up approach includes first looking at the smaller sub-problems, and then solving the larger sub-problems using the solution to the smaller problems.
This approach avoids memory costs that result from recursion.
But both the top-down approach and bottom-up approach in dynamic programming have the same time and space complexity. So in the end, using either of these approaches does not make much difference.
Just a quick note: dynamic programming is not an algorithm. But I have seen some people confuse it as an algorithm (including myself at the beginning).
It is used only when we have an overlapping sub-problem or when extensive recursion calls are required. It is a way to improve the performance of existing slow algorithms.
This means, also, that the time and space complexity of dynamic programming varies according to the problem.
Dynamic Programming Example
Now let us solve a problem to get a better understanding of how dynamic programming actually works.
Consider the problem of finding the longest common sub-sequence from the given two sequences.
⇒ ‘gtcab’ and ‘gxtxab’
We can solve this problem using a naive approach, by generating all the sub-sequences for both and then find the longest common sub-sequence from them.
But the time complexity of this solution grows exponentially as the length of the input continues increasing.
So, how do we know that this problem can be solved using dynamic programming?
For the two strings we have taken, we use the below process to calculate the longest common sub-sequence (LCS).
As we can see, here we divide the main problem into smaller sub-problems. Let us check if any sub-problem is being repeated here.
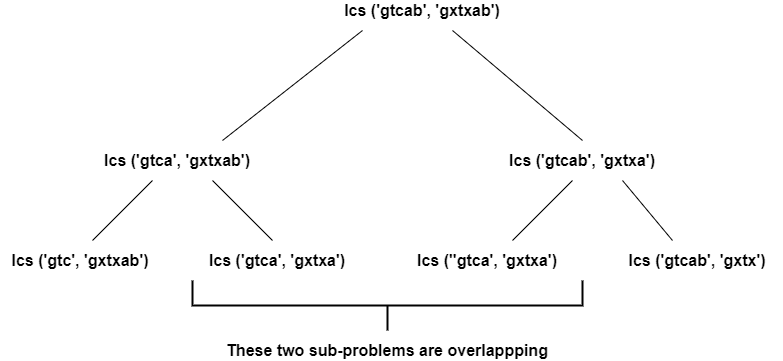
We can see here that two sub-problems are overlapping when we divide the problem at two levels.
If we further go on dividing the tree, we can see many more sub-problems that overlap. So we conclude that this can be solved using dynamic programming.
Next, let us look at the general approach through which we can find the longest common sub-sequence (LCS) using dynamic programming.
How to fill the matrix?
We will use the matrix method to understand the logic of solving the longest common sub-sequence using dynamic programming.
Here we will only discuss how to solve this problem – that is, the algorithm part. And for that we use the matrix method.
Look at the below matrix. We have filled the first row with the first sequence and the first column with the second sequence.
Then we populated the second row and the second column with zeros for the algorithm to start. We denote the rows with ‘i’ and columns with ‘j’.
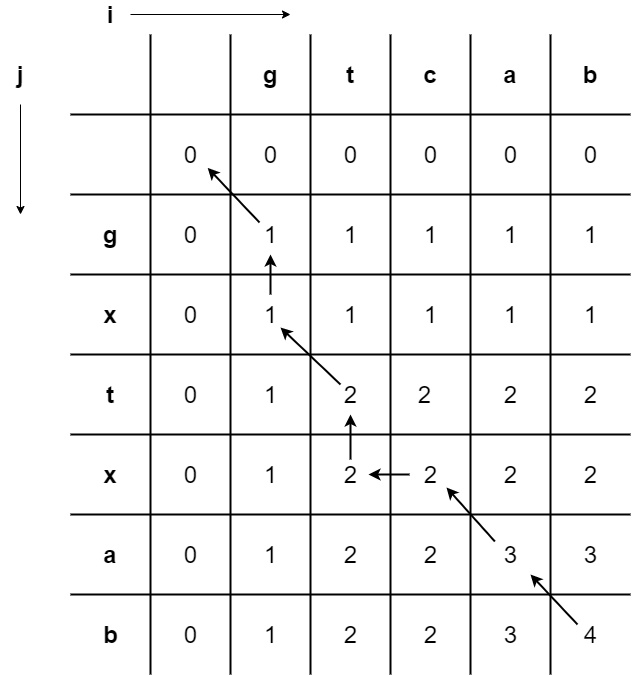
Now we move on to fill the cells of the matrix. Compare the two sequences until the particular cell where we are about to make the entry.
The length/count of common sub-sequences remains the same until the last character of both the sequences undergoing comparison becomes the same.
If the sequences we are comparing do not have their last character equal, then the entry will be the maximum of the entry in the column left of it and the entry of the row above it.
When the last characters of both sequences are equal, the entry is filled by incrementing the upper left diagonal entry of that particular cell by 1.
The logic we use here to fill the matrix is given below:
if(input[i]==input[j]) //Check if last characters are equal
T[i][j]=T[i-1][j-1]+1 //Entry is incremental of upper left element
else //If the last character are not equal
T[i][j]=max(T[i-1][j], T[i][j-1]) //Entry is max of element to its left and top
The bottom right entry of the whole matrix gives us the length of the longest common sub-sequence.
Finding the longest common sub-sequence
In order to get the longest common sub-sequence, we have to traverse from the bottom right corner of the matrix. Then we check from where the particular entry is coming.
That is, we can check whether it is the maximum of its left and top entry or else is it the incremental entry of the upper left diagonal element?
We repeat this process until we reach the top left corner of the matrix. The sub-sequence we get by combining the path we traverse (only consider those characters where the arrow moves diagonally) will be in the reverse order.
We have to reverse this obtained sequence to get the correct longest common sub-sequence. So in this particular example, the longest common sub-sequence is ‘gtab’.
I have made a detailed video on how we fill the matrix so that you can get a better understanding. You can find it here: Video Explanation.
What did we learn?
In this article, we learned what dynamic programming is and how to identify if a problem can be solved using dynamic programming.
Then we went on to study the complexity of a dynamic programming problem.
Next we learned how we can solve the longest common sub-sequence problem using dynamic programming.
I hope you enjoyed it and learned something useful from this article.
If you found this post helpful, please share it. If you have any feedback, feel free to contact me on Twitter.

