Euclidian Algorithm: GCD (Greatest Common Divisor) Explained with C++ and Java Examples

For this topic you must know about Greatest Common Divisor (GCD) and the MOD operation first.

Greatest Common Divisor (GCD)

The GCD of two or more integers is the largest integer that divides each of the integers such that their remainder is zero.

Example-
GCD of 20, 30 = 10  (10 is the largest number which divides 20 and 30 with remainder as 0)
GCD of 42, 120, 285 = 3  (3 is the largest number which divides 42, 120 and 285 with remainder as 0)

"mod" Operation

The mod operation gives you the remainder when two positive integers are divided. We write it as follows-
A mod B = R

This means, dividing A by B gives you the remainder R, this is different than your division operation which gives you the quotient.

Example-
7 mod 2 = 1  (Dividing 7 by 2 gives the remainder 1)
42 mod 7 = 0  (Dividing 42 by 7 gives the remainder 0)

With the above two concepts understood you will easily understand the Euclidean Algorithm.

Euclidean Algorithm for Greatest Common Divisor (GCD)

The Euclidean Algorithm finds the GCD of 2 numbers.

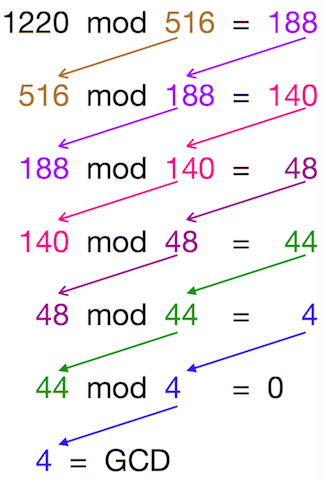
You will better understand this Algorithm by seeing it in action. Assuming you want to calculate the GCD of 1220 and 516, lets apply the Euclidean Algorithm-

Assuming you want to calculate the GCD of 1220 and 516, lets apply the Euclidean Algorithm-

Pseudo Code of the Algorithm-
Step 1:  Let  a, b  be the two numbers
Step 2:  a mod b = R
Step 3:  Let  a = b  and  b = R
Step 4:  Repeat Steps 2 and 3 until  a mod b  is greater than 0
Step 5:  GCD = b
Step 6: Finish

JavaScript Code to Perform GCD-

function gcd(a, b) {
  var R;
  while ((a % b) > 0)  {
    R = a % b;
    a = b;
    b = R;
  }
  return b;
}

JavaScript Code to Perform GCD using Recursion-

function gcd(a, b) {
  if (b == 0)
    return a;
  else
    return gcd(b, (a % b));
}

C code to perform GCD using recursion

int gcd(int a, int b) 
{ 
    // Everything divides 0  
    if (a == 0) 
       return b; 
    if (b == 0) 
       return a; 
  
    // base case 
    if (a == b) 
        return a; 
  
    // a is greater 
    if (a > b) 
        return gcd(a-b, b); 
    return gcd(a, b-a); 
}

C++ Code to Perform GCD-

int gcd(int a,int b) {
  int R;
  while ((a % b) > 0)  {
    R = a % b;
    a = b;
    b = R;
  }
  return b;
}

Python Code to Perform GCD using Recursion

def gcd(a, b):
  if b == 0:
    return a:
  else:
    return gcd(b, (a % b))

Java Code to Perform GCD using Recursion

static int gcd(int a, int b)
{
  if(b == 0)
  {
    return a;
  }
  return gcd(b, a % b);
}

You can also use the Euclidean Algorithm to find GCD of more than two numbers. Since, GCD is associative, the following operation is valid-  GCD(a,b,c) == GCD(GCD(a,b), c)

Calculate the GCD of the first two numbers, then find GCD of the result and the next number. Example-  GCD(203,91,77) == GCD(GCD(203,91),77) == GCD(7, 77) == 7

You can find GCD of  n  numbers in the same way.

What is the Extended Euclidean Algorithm?

This is an extension of Euclidean algorithm. It also calculates the coefficients x, y such that

ax+by = gcd(a,b)

x and y are also known as coefficients of Bézout's identity.

c code for Extended Euclidean algorithm

struct Triplet{
	int gcd;
	int x;
	int y;
};
Triplet gcdExtendedEuclid(int a,int b){
	//Base Case
	if(b==0){
		Triplet myAns;
		myAns.gcd = a;
		myAns.x = 1;
		myAns.y = 0;
		return myAns;

	}
	Triplet smallAns = gcdExtendedEuclid(b,a%b);
	//Extended euclid says

	Triplet myAns;
	myAns.gcd = smallAns.gcd;
	myAns.x  = smallAns.y;
	myAns.y = (smallAns.x - ((a/b)*(smallAns.y)));
	return myAns;	
}