The finite state machine (FSM) is a software design pattern where a given model transitions to other behavioral states through external input.
Understanding the Finite State Machine
A FSM is defined by its states, its initial state and the transitions.
The power of FSM comes from the ability to clearly define different behaviors in different conditions. Usually FSM is used with looping behavioral scripts which constantly evaluate the current situation in a loop or with events.
To help form an image of how this might be applied, a coffee machine will be used as an example of a finite state machine. We will also cover a state diagram to visualise the FSM and provide coding examples.
State Diagram
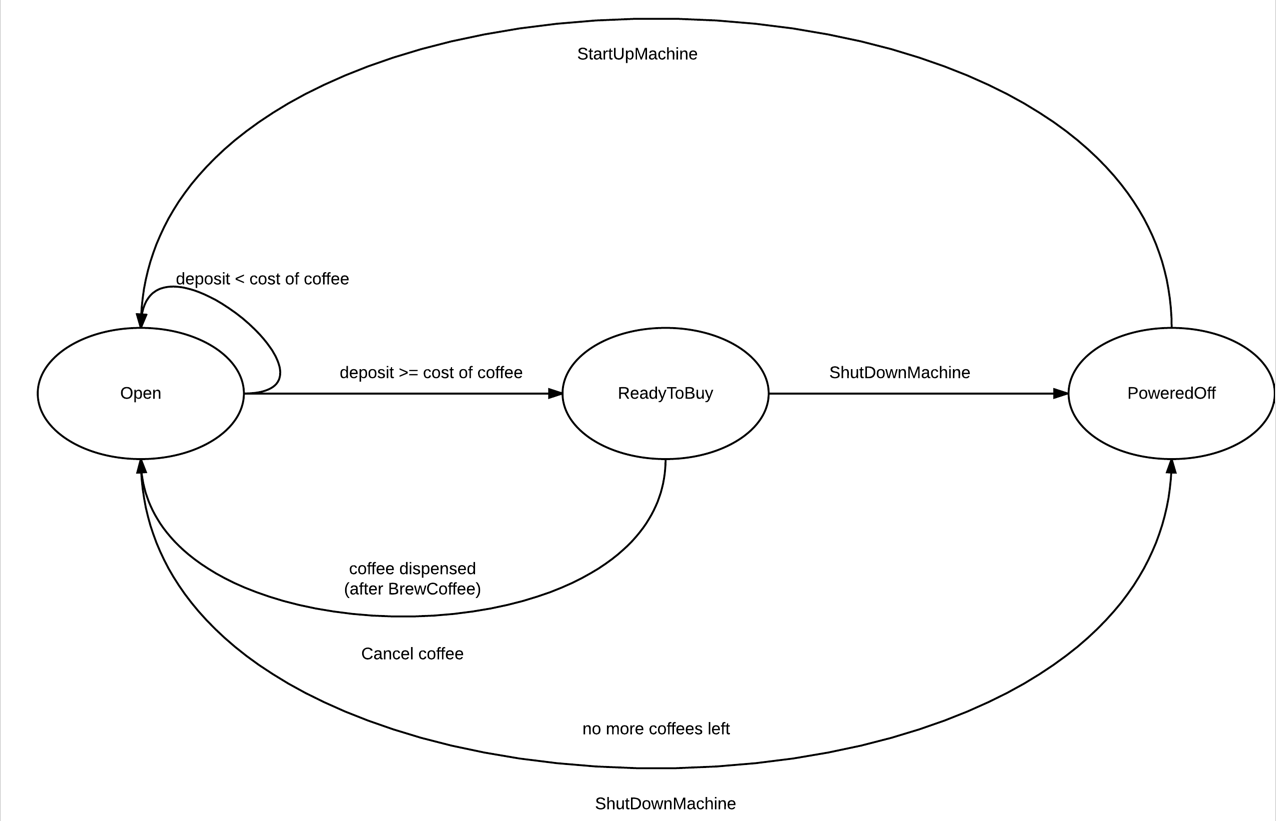
This diagram shows three possible states for the coffee machine:
- Open
- ReadyToBuy
- PoweredOff
The lines between these states show which transitions are possible between states and in which direction. These transitions have conditions for when the FSM needs to change between states.
- StartUpMachine From the PoweredOff state to the Open state the machine has to start up. This is done manually in this case.
- deposit >= cost of coffee The FSM evaluates the amount of deposited cash either in a loop or when the amount changes (recommended in this case) If you deposit enough cash into the coffee machine, the FSM will go from ‘Open’ to ‘ReadyToBuy’.
- ShutdownMachine The machine will automatically go from Open to PoweredOff through the ShutDownMachine method if the condition ‘no more coffees left’ is met.
- DispenseCoffee In the ReadyToBuy state the user can buy a coffee whereafter it will be brewed and dispensed. The condition is when the BuyCoffee event (!Link to observer pattern!) fires. (not shown in diagram)
- CancelCoffee If the user opts to cancel, the machine will go from ReadyToBuy to Open.
- ShutDownMachine The machine will go to PoweredOff state
States
In every state there is defined behavior which will only be executed when the object is in that state. For instance, during PoweredOff the coffee machine won’t brew coffee before it’s powered on, during the Open state it will wait either until there’s enough cash inserted, until the power down command is given, or until it runs out of coffee. During this Open state it can do routines such as cleaning which won’t happen in other states.
Initial State
Every FSM has an initial state, this means which state it starts in when it is created and has to be defined when constructed or instantiated. Of course it’s possible to directly change state if conditions are met.
Transitions
Every state either constantly evaluates if it should transition to another state or will transition to another state based on a triggered event.
DFA and NFA
There are two types of finite automaton, Deterministic (DFA) and Nondeterministic (NFA). Both of them accept regular languages and operate more or less in the same way described above however with some differences.
A DFA accepts or rejects a string of symbols and only produces one unique computation or automaton for each input string. Deterministic refers to the uniqueness of the computation. A Finite State Machine is called a DFA if it obeys the following rules:
- Each of its transitions is uniquely determined by its source state and input symbol
- Reading an input symbol is required for each state transition.
An NFA does not need to obey these restrictions, meaning that each DFA is also an NFA. And since they both only recognize regular languages, each NFA can be converted into an equivalent DFA using the powerset construction algorithm.
So what sort of rules can we expect to find in NFAs but not DFAs ?
- An NFA can have an empty string transition (generally denoted by an epsilon). Meaning that when at a certain state with an epsilon for a transition rule, the machine can transition to the next state without reading an input symbol
- In an NFA, each pair of state and transition symbol can have multiple destination states as opposed to the unique destinations of pairs in DFAs
- Each pair of state and transition symbol produces a ‘branch’ of computation for each of its possible destination creating some sort of a multithreaded system.
- A DFA will reject the input string if it lands on any state other than the acceptance state. In an NFA, we only need one ‘branch’ to land on an acceptance state in order to accept the string.
If you want to learn more, here's a great in-depth guide on state machines.
