Fraction Math: How to Do Fractions for Beginners

We deal with fractions every day. But what exactly is a fraction? How do we get to know them better? In this tutorial we will explore the basics and practice together, so fractions can become valuable helpers in everyday life and beyond.

Part 1. Fraction as a share

Let's imagine a whole pie divided into 4 equal parts. One part is shaded red.

One red part out of four equal parts means 1/4 of a whole is shaded. If we think of equal parts of a whole as shares, one share of a pie here is shaded red.

The number 1 above the line is called a Numerator. It shows how many shares are shaded. The number 4 below the line is called a Denominator. It shows how many equal shares a whole is divided into. Let's look at another example.

The new pie above is divided into 6 equal shares. Therefore, the denominator will equal 6. Out of these 6 equal shares 3 are shaded red. Therefore, the numerator will equal 3. In other words, 3/6 of the pie is shaded.

Now let's test what we have learned so far. As you know, there are 24 hours in a whole day. If you spent 6 hours studying, what fraction of the day did you spend studying?

A day is divided into 24 equal shares called hours. So the Denominator will be 24. Think of the 6 hours spent studying as 6 shaded shares of the pie. That will make the Numerator equal 6. The fraction we are looking for is 6/24.

Part 2. Simplifying fractions

Remember the pie from previous example? It had 3/6 of it shaded red. Let's add two new pies and look at them together.

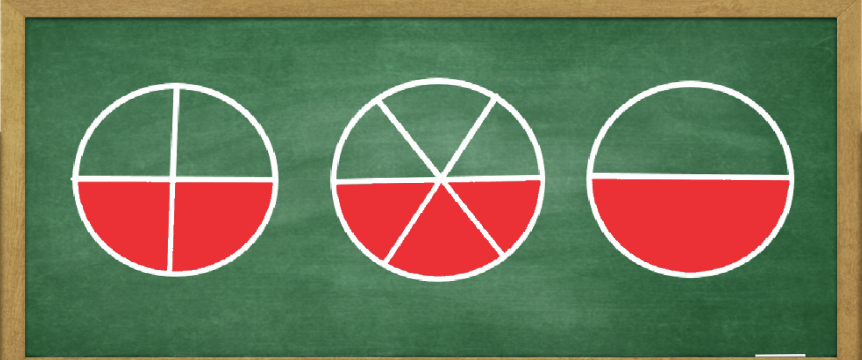
The first pie is divided into 4 shares and two are shaded red. But as we can see that's half the pie. The second pie is divided into 6 shares and three are shaded red. Half of the pie again. Finally, the third pie is divided into two halves and one half is shaded red.

Since it's half a pie that's shaded in either case, we can conclude that the fractions are equal: 2/4 = 3/6 = 1/2.

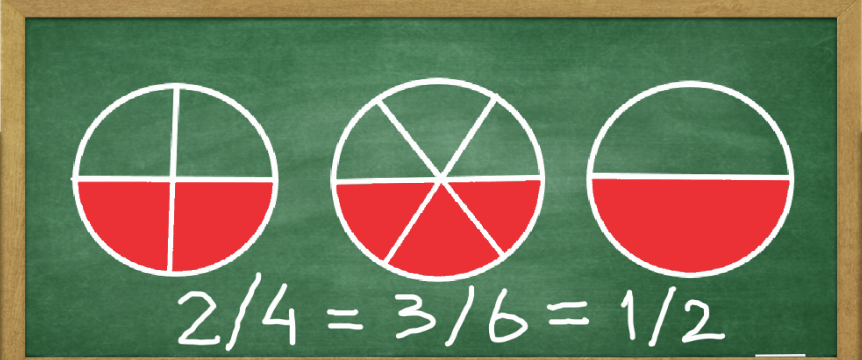
Finally, by multiplying or dividing both the numerator and denominator by the same number, the fraction will stay the same (except the case when division is by zero, which is outside of the scope of this article and will not be considered here).

This rule helps simplify fractions and makes using them easier. As an example, let's consider 4/12. Dividing numerator and denominator by 4 gives us (4 : 4) / (12 : 4) = 1 / 3. It's time to test your knowledge.

Part 3. Comparing fractions

When we see two pieces of a pie, we can usually tell which one is larger. Similarly with fractions, there is a simple way of comparing them to each other.

Say we need to compare 1/3 and 2/7. Since they have different denominators, they have a different number of parts. So the First step must be to find the common ground. We do it by finding a common denominator.

One of the methods for finding a common denominator of two or more fractions is to multiply the denominators with each other. 3 times 7 = 21.

Now that we found the common denominator, we need to replace each fraction's own denominator with the common denominator.

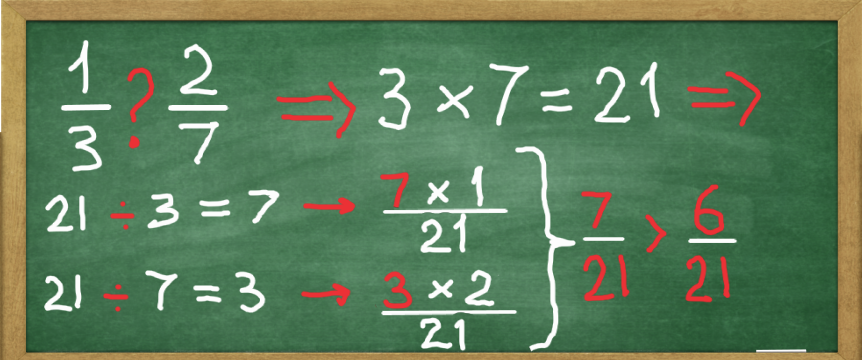
The first fraction is 1/3, so we divide 21 by 3 and resulting 7 gets multiplied by that fractions numerator. Since the numerator equals 1, we get 7 times 1 = 7.

The second fraction is 2/7, so 21 divided by 7 results in 3. Multiplying 3 times this fractions numerator, gives us 3 times 2 = 6.  

Now that the fractions have the same denominator, we can finally compare them. 7 shares is more than 6 shares, therefore 7/21 is greater than 6/21.

The mathematical symbol denoting our result is the > sign. 7/21 > 6/21. It is read as  "greater-than." The symbol denoting lesser-than looks like this: <. We can rewrite our result like this: 6/21 < 7/21.

Part 4. Adding fractions

To add fractions, we again need to find a common denominator. Let's look at the following example.

We need to add 2/7 and 3/9. The common denominator is 7 times 9 = 63. The next step would be to replace each fraction's own denominator with the common one.

For the first fraction, 63 divided by 7 = 9 and 9 times 2 = 18. The result is 18/63. For the second one, 63 divided by 9 = 7 and 7 times 3 = 21. The result is 21/63.

Next, we add the numerators. 18 plus 21 = 39, which leaves us with the sum of 39/63.

As a useful habit, always check if the resulting fraction can be further simplified.

We know that 39 is evenly divisible by 3. 63 is also evenly divisible by 3. Since both numerator and denominator are divided by the same number, the fraction will remain the same. 39 divided by 3 = 13 and 63 divided by 3 = 21. Our final result is 13/21.

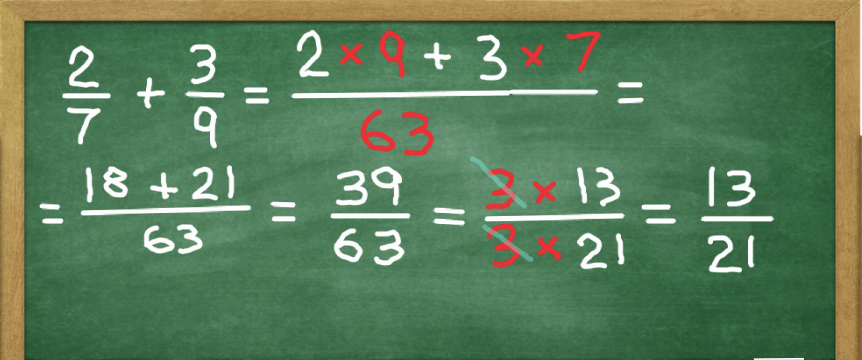
What if we need to add mixed numbers? To add mixed numbers, we first add the whole numbers together and then the fractions.

For example, to add 1 and a half to 2 and a half, add 1 and 2 = 3, then add 1/2 and 1/2 = 1. Finally, add 3 and 1 = 4. Let's have some practice and remember how to simplify results.

Part 5. Subtracting fractions

We'll start with two simple fractions. Subtract 1/3 from 3/5. As in the case of addition, we need to find a common denominator. So if we multiply our denominators, that equals 3 times 5 = 15.

Next, we replace old denominators with the common one.  

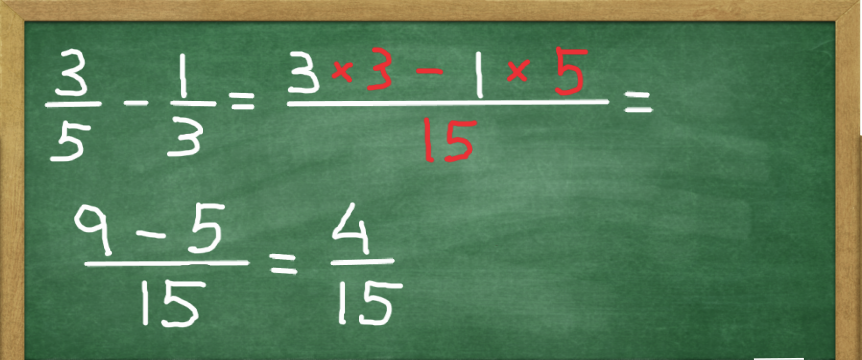
Then we need to find our numerators. For the first fraction, 15 divided by 5 = 3 and 3 times 3 = 9. The result is 9/15. For the second one, 15 divided by 3 = 5 and 5 times 1 = 5. The result is 5/15.

The last step is to subtract the adjusted numerators: 9 minus 5 = 4. The resulting fraction equals 4/15.  

Let's now look at the case when we need to subtract a fraction from a whole number. Let's begin with 1 - 2/7.

You remember from previous sections that a whole number is like a pie that is completely shaded. Thus, if a pie is divided into 3 parts, all 3 parts are shaded. If it is divided into 7 parts, then 7 parts will be shaded. So, 1 = 3/3 = 7/7 etc.

Since we need to subtract 2/7, we'll turn 1 whole into 7/7 to make our task easy. 7/7 minus 2/7 = 5/7. If the whole number is other than 1, we write it as a mixed number and follow the steps from the last example.

So let's subtract 2/7 from 3.

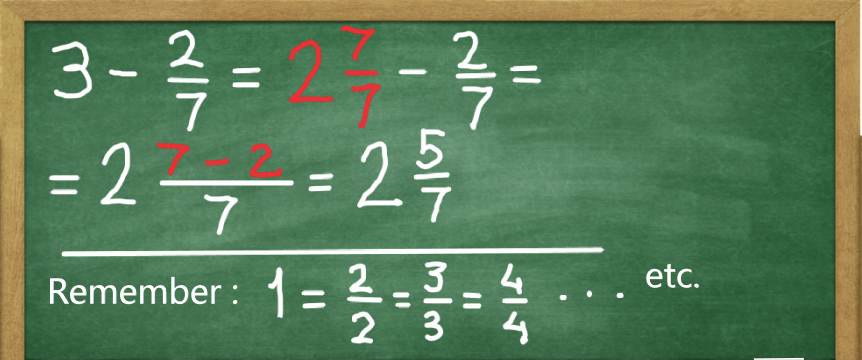
Often, as a result of calculations, we may end up with a fraction where the numerator is greater than or equal to the denominator. Such fractions are called improper fractions. For example 5/3 (five thirds), 7/2 (seven halves) and so on. They can be converted to mixed numbers and vice versa.

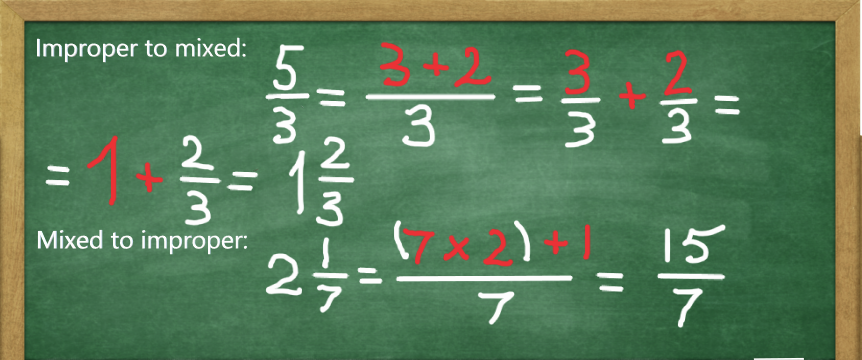
All the rules covered so far apply to improper fractions as well.

Part 6. Multiplying fractions

Suppose we need to multiply two fractions, 2/5 times 3/7. The numerator of the product will be the product of the numerators of these fractions: 2 times 3 = 6. The denominator of the product will be the product of denominators of these fractions: 5 times 7 = 35. Thus, 2/5 times 3/7 = 6/35.

If we need to multiply a fraction by a whole number, the numerator of the product will be the product of the numerator of the fraction and that whole number. The denominator of the product will remain the same as the denominator of the fraction.

For example, 3/10 times 5 = 15/10. To simplify, we divide the numerator and denominator by 5 and get 3/2.

Finally, if we need to multiply mixed numbers, first we convert them to improper fractions, then multiply them as we did above. The example below shows the steps.

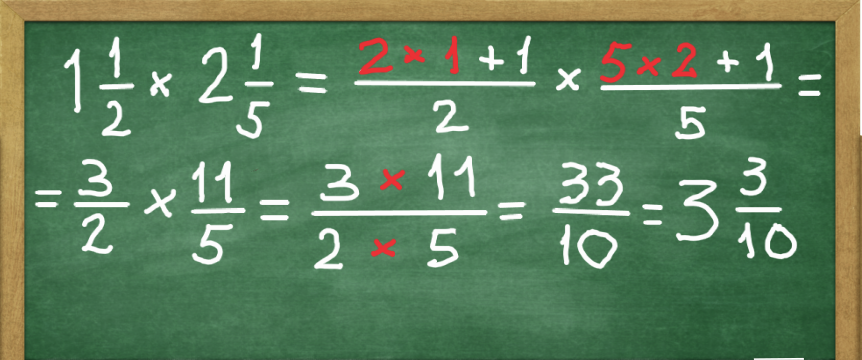
Part 7. Dividing fractions

To divide fractions, flip the divisor so its numerator becomes the new denominator and denominator becomes the new numerator. Then just multiply the fractions like we did before.

For example, divide 3/7 by 2/5. After flipping, 2/5 becomes 5/2 and we end up multiplying 3/7 times 5/2 = 15/14.

To divide fraction by a whole number, we invert that number and it becomes 1 divided by that number.

For instance, 2 becomes 1/2, 9 becomes 1/9 etc. Next, we multiply as above. As you probably guessed already, dividing mixed numbers works the same way. Let's look at the example below.

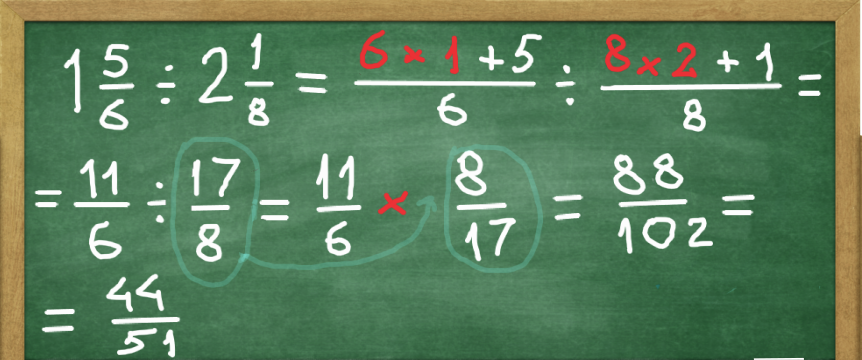
Let's test your knowledge.

Part 8. Some practical examples

In order to find a fraction of some number, we need to multiply the given number by that fraction.

Imagine, your school textbook has 200 pages. If you read 3/5 of the textbook, how many pages have you read? We are given the number which equals 200. To find 3/5 of 200, we multiply 200 times 3/5 and get  120 pages.

Solve the next question on your own. My birthday cake had 12 pieces. A few friends came by and enjoyed 2/3 of the cake. How many pieces did my friends have?

Finally, there is one more case I want to explore. What if we know what a given fraction of some number equals and we need to find that number?

For example, we know my friends had 8 pieces of the birthday cake and that was 2/3 of the whole cake. How many pieces did the cake have in the beginning? In order to find that whole number, we need to divide 8 by 2/3, which is 12.

Solve the next question on your own. A race car drove 900 meters on a track, which is 3/5 of the whole distance. What's the length of the race track?