by Subhan Nadeem
How Bitcoin mining really works

As Bitcoin approaches mainstream adoption and recognition, its fundamental security model, characterized as mining, is being put under the spotlight and scrutinized more and more everyday.
People are increasingly concerned about and interested in the environmental impact of Bitcoin mining, the security and degree of decentralization of the underlying model, and even the potential impact of a quantum computing breakthrough on the future of Bitcoin and other cryptocurrencies.
Often times, proof-of-work is described as a “cryptographic puzzle,” but what is that puzzle, really?
In order to truly understand these questions (and any possible answers), you need to have a fundamental understanding Bitcoin mining itself and its evolution.
This article will explore all the technical components and moving parts of proof-of-work, and how they seamlessly synchronize with one another to allow Bitcoin to be the decentralized platform it is today.
Why Mining Works: Cryptographic One-Way Hashing
The Bitcoin blockchain is often described as a database that is cryptographically secure and, subsequently, immutable. The underlying technology that powers this immutability and security is cryptographic hashing.
A cryptographic hash function is a mathematical function that, simply put, takes any input and maps it to a fixed-size string.
However, there are four special properties of these functions that make them invaluable to the Bitcoin network. They are:
- Deterministic — for any input into the cryptographic hash function, the resulting output will always be the same.
- Fast — Computing the output of the hash function, given any input, is a relatively fast process (doesn’t need heavy computation)
- Unique — Every input into the function should result in a completely random and unique output (in other words, no two inputs result in the same output)
- Irreversible — Given an output of a hash function, the original input is unable to be obtained
These rules provide the foundation that enables Bitcoin mining to secure the network.
In particular, the creator of the Bitcoin protocol, Satoshi Nakomoto, chose to use the SHA-256 hash function as the basis for Bitcoin mining. This is a specific cryptographic hash function that has been mathematically proven to hold the above properties. It always outputs a 256 bit number (the most basic unit of computation), which is usually represented in the hexadecimal number system with 64 characters for human-readability.
The output of the SHA-256 function is usually referred to as the hash of its input.
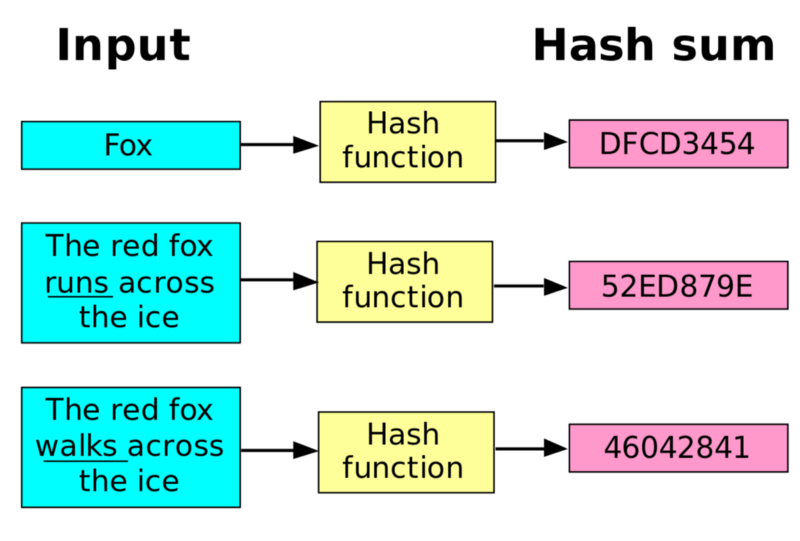
Here is an example of a SHA-256 function input and output (you can try it out yourself here):
Input to SHA-256:
<Bitcoin Transaction>
Output to SHA-256:
77077b1f4c3ad44c83dc0bdb8d937e9b71c0ef07a35c2664bb7da85be738eacfInterestingly enough, in the majority of places where hashing is used in the Bitcoin protocol, double hashing is used. This means that the output of the original SHA-256 function is then put right back into the SHA-256 function to obtain another output. Here is what that process looks like:
Input to SHA-256(first round):
<Bitcoin Transaction>
Output (first round):
77077b1f4c3ad44c83dc0bdb8d937e9b71c0ef07a35c2664bb7da85be738eacf
Input to SHA-256 (second round):
77077b1f4c3ad44c83dc0bdb8d937e9b71c0ef07a35c2664bb7da85be738eacf
Output (second round and final result):
3c6c55b0e4b607b672b50f04e028a6951aed6dc97b91e103fb0f348c3f1dfa00Double hashing is used to safeguard against birthday attacks. A birthday attack is a scenario where an attacker is able to produce the same hash as another input by using a completely different input (called a collision). This breaks the third property of uniqueness. Without it, two completely different Bitcoin blocks may be represented by the exact same hash, allowing attackers to potentially switch out blocks.
With the SHA-256 function, the probability of this attack happening is infinitely small. If it wasn’t close to impossible, SHA-256 would be considered broken.
However, other hash functions have been “broken” in the past. In order to safeguard against this happening to SHA-256 in the future (and effectively breaking the security model of Bitcoin) it’s best to hash the hash. This halves the probability of a collision occurring, making the protocol that much more secure.
At a very high level, Bitcoin mining is a system in which all Bitcoin transactions are sent to Bitcoin miners. Miners select one megabyte worth of transactions, bundle them as an input into the SHA-256 function, and attempt to find a specific output the network accepts. The first miner to find this output and publish the block to the network receives a reward in the form of transaction fees and the creation of new Bitcoin.
Let’s take things a step further and dive into the Bitcoin blockchain itself to see what exactly it is that miners do to make the network secure.
Bitcoin Mining: A Technical Introduction
Mining was introduced as the solution to the double-spend problem. If I have 1 Bitcoin and I send it to Bob, and then try sending that same Bitcoin to Alice, the network ensures that only one transaction will be accepted. It does this through the well-known process called mining.
Before diving into the technical details, its important to understand why mining is necessary to secure the network. As fiat currency exists now, the currency we hold is created and validated by a federal reserve. Because Bitcoin operates under the rigid assumption of decentralization and consensus, no central authority can exist that validates and time-stamps the issuance of that currency and validation of any transactions that occur with that currency.
Satoshi Nakamoto proposed the only known solution at the time to solving this validation problem in a consensus-oriented system. Titled in the Bitcoin whitepaper as proof-of-work, this scheme elegantly justifies that transactions are validated by those who are willing to expend enough physical computational energy and time to do so, while simultaneously introducing an incentive to induce market competition. This competition enables the property of decentralization to emerge and thrive organically within the ecosystem.
A Look Inside a Block
A Bitcoin block consists primarily of two components:
1. Transactions, in the form of a merkle tree
Mining computers collect enough transactions to fill a block and bundle them into a merkle tree.
A merkle tree is a relatively simple concept: transactions lie at the bottom of the tree as leaves and are hashed using the SHA-256 function. The combination of two leaf transactions are hashed again using the SHA-256 function to form a parent of the leaves. This parent is continuously hashed upwards in combination with other parents of hashed transactions, until a single root is created. The hash of this root is effectively a unique representation of the transactions that are underneath it.
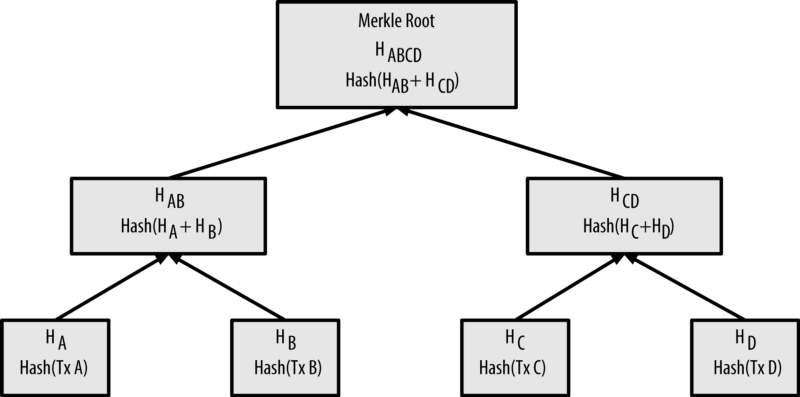
The root of the merkle tree is a combination of the hashes of every transaction in the tree.
Recall that for any any input to a hash function, the output is entirely unique. Therefore, once most nodes on the network receive a mined block, the root of the merkle tree hash acts as an unchangeable summary of all the transactions in that given block.
If a malicious actor were to try and change the contents of a transaction in a block, its hash would be changed. This change of a hash would be propagated up the transaction’s merkle tree until the hash of the root is changed. Any node can then quickly catch this malicious act by comparing the root of the changed block’s merkle tree to that of a valid block’s merkle tree.
2. The block header
The block header is a summary of the contents of the block itself. It contains the following six components:
- The version of software the Bitcoin client is running
- The timestamp of the block
- The root of its containing transactions' merkle tree
- The hash of the block before it
- A nonce
- The target
Remember that the root of the transaction merkle tree acts as an effective summary of every transaction in the block without having to look at each transaction.
The hash of the previous block before it allows the network to properly place the block in chronological order. This is where the term blockchain is derived from — each block is chained to a previous block.
The nonce and target are what make mining tick. They are the basis for solving the SHA-256 puzzle that miners need to solve.
Please note that all of this data in the block header is compressed into 80 bytes using a notation called little-endian, making the transfer of block headers between nodes a trivially efficient process. For the purposes of this explanation, we’ll ignore this compression and assume data is in its original form.
Explaining the Mining Problem
The target stored in the block header is simply a numeric value stored in bits. In traditional base 10 notation, this target ranges anywhere between 0 to somewhere in the range of 2²²⁴ (a 67+ digit number), depending on how many miners are competing to solve this problem at the same time.
Recall that the output of SHA-256 is just a number. The goal of a miner is to take the current block’s header, add a random number to it called the nonce, and calculate its hash. This numeric value of the hash must be smaller than the target value.
That’s all there is to it. But it’s much easier said than done.
Recall the first property of SHA-256: an input into a hash function will always result in the same output. Therefore, if the miner took the block header, hashed it, and realized that the hash value wasn’t less than the target, they would have to change the input somehow in order to try finding a hash below the target value.
This is where the nonce comes in.
The miner adds a number (starting from 0), called the nonce, to the block header, and hashes that value. If the hash value isn’t less than the target, the miner will increment the nonce by 1, add it again to the block header, and hash that changed value. This process is repeated continuously until a hash less than the target value is found.
A Mining Example
Here’s a rough approximation of what made up the first block header:
- The merkle root of the transaction in the Genesis block:
Merkle Root:
4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b- The first known Bitcoin version:
0.1.0 - The timestamp of the block:
2009–01–03 18:15:05 - The target (this is also the highest the target will ever be):
Target:
0x00000000FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF- No previous block hash — this was the first block, and so this is a unique case
The final block header after adding its components together:
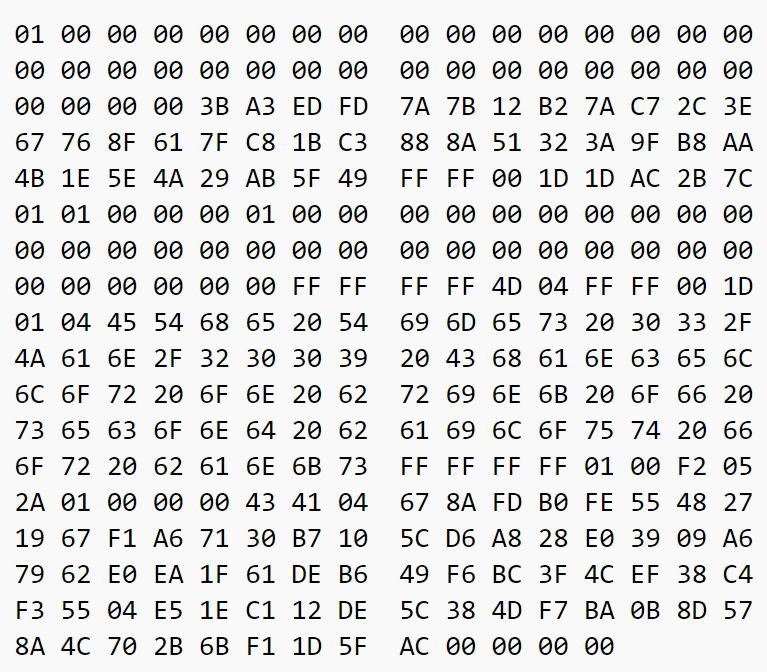
Let’s take this large header and compute the double-hash:
SHA-256 of header:
7d80bd12dfdccbdde2c41c9f406edfc05afb3320f5affc4f510b05a3394e1c91
SHA-256 of the previous result (final result):
c5aa3150f61b752c8fb39525f911981e2f9982c8b9bc907c73914585ad2ef12bBoth the target and the output hash are incredibly large numbers when converted to base 10 (remember, over 67 digits long). Instead of trying to demonstrate the comparison of the two here, the following Python function handles the comparison instead:
def isBlockHashLessThanTarget(blockHash, target):
return int(blockHash, 16) < int(target, 16)True is returned if the hash is less than the target, false otherwise.
Here is the result with our target and block hash:

Now we take the original block hexadecimal value and add 1 to it. Here is the following result:

We then run the same hashing algorithm and comparison on this changed data. If its not below the target, keep repeating.
Once a successful hash is found, the latest nonce used to find this solution is saved within the block.
The listed nonce on the Genesis block is 2,083,236,893.
This means Satoshi Nakomoto iterated through this process over 2 billion times before he found a hash that was acceptable.
I’ve written a small Python implementation of this Genesis block mining process that can be found on my GitHub.
subhan-nadeem/bitcoin-mining-python
bitcoin-mining-python - A Python implementation of the Bitcoin mining algorithm
github.com
See how long it would take for you to successfully mine the Genesis block!
A Caveat: extraNonce
The nonce value in a block header is stored as a 32-bit number. This means that the highest nonce anybody is able to achieve is 2³² (approximately 4 billion). After 4 billion iterations, the nonce is exhausted, and if a solution is not found, miners are once again stuck.
The solution to this is to add a field to the coinbase (the transaction contents of a block, stored as the merkle tree) called the extraNonce. The size of this extraNonce is only limited by the size of block itself, and so it can be as large as miners wish as long as the block size is within protocol limits.
If all 4 billion possible values of the nonce are exhausted, the extraNonce is added and incremented to the coinbase. A new merkle root and subsequently new block header are calculated, and the nonce is iterated over once again. This process is repeated until a sufficient hash is found.
It’s best to avoid adding the extraNonce until the nonce is exhausted, because any change to the extraNonce changes the merkle tree. This requires extra computation in order to propagate the change upwards until a new root of the merkle tree is calculated.
The Miner Reward
A miner who successfully publishes a block the fastest is rewarded brand new Bitcoin, created out of thin air. That reward currently stands at 12.5 BTC. Just how do these Bitcoins come into existence?
Each miner simply adds a new output transaction to their block that attributes 12.5 Bitcoins to themselves before beginning to mine the block. The network protocol will accept this special transaction as valid upon receiving a newly validated block. This special transaction is called a generation transaction.
Its the miner’s responsibility to add this transaction into the block before mining it. There has been at least one case where miners forgot to add the reward to the transaction before mining a block, effectively destroying 12.5 BTC!
Validating Proof-of-Work
Let’s say our miner has found a hash that is less than the target. All this miner has to do is publish the mined block with the original six components to any connected nodes.
This node receiving the block will first verify the transaction set, ensuring all transactions are valid (for example, all transactions are appropriately signed, and coins aren’t being double-spent and/or being created out of thin air).
It will then simply double-hash the block header and ensure the value is below the block’s included target value. Once the block is deemed valid, the new node will continue to propagate this block across the network until every node has an up-to-date ledger.
As you can see, newly published blocks can easily be verified by any given node. However, publishing a valid block to the network requires an incredibly large amount of computational power (thus, electricity and time). This asymmetry is what allows the network to be secured while simultaneously allowing individuals who wish to conduct economic activity on the network to do so in a relatively seamless manner.
The Block Time and Adjusting the Target
As the first miners began mining, they each monitored the block time. Each Bitcoin block has a set block time of 10 minutes. What this means is that given the current level of computing power (network hashrate) on the network, nodes will always expect newly validated blocks to be produced every 10 minutes on average.
We can reasonably expect blocks to be produced within 10 minutes because the probability of finding a block, given the network hashrate, is known.
For example, let’s take the easiest target that’s ever existed in Bitcoin: the genesis block. The probability of any single hash being less than the easiest target is 1 in 2³². That’s one in over four billion. Therefore, we can reasonably expect somebody to run 2³² iterations of the mining problem in order to find a proper hash. Nodes on the network expected four billion of these iterations to be run across all miners on the network every 10 minutes.
If, over a large sample size of blocks, blocks start appearing faster than 10 minutes, this is a pretty clear indication that nodes on the network are iterating through four billion hashes much faster than 10 minutes. This situation prompts every node to adjust the target proportionally based on the increase (or decrease) in network power to ensure blocks continue to be produced every 10 minutes.
In actuality, nodes on the network monitor the block time across 2016 blocks, which comes out to exactly two weeks. Every two weeks, the total block time is compared to the expected block time (which is 20160 minutes).
To obtain the new target, simply multiply the existing target by the ratio of the total actual block time over the last two weeks to get the expected block time. This will adjust the target proportionally to the amount of entering or exiting computing power on the network.

The block time and the ability to easily calculate the probability of finding a valid block lets nodes easily monitor and determine the total hashpower on the network and adjust the network. No matter how much computing power is added to the network or how quickly its added, on average the block time will always remain at 10 minutes.
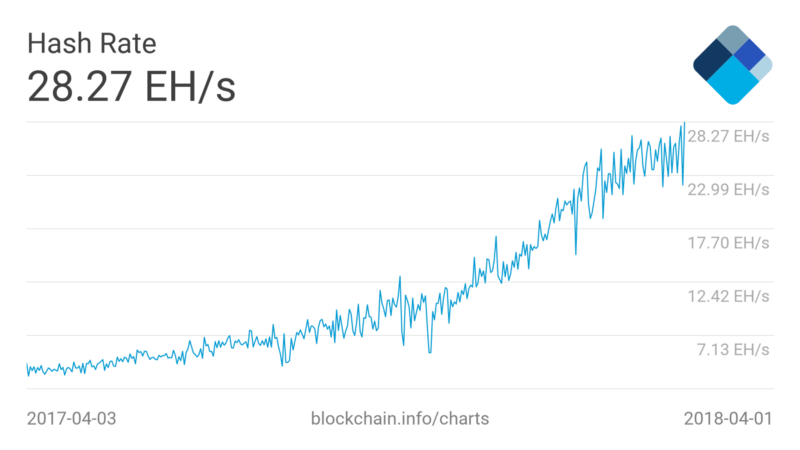
The current total hash rate on the network is 28.27 exahash per second. That’s 28.27 x 10¹⁸ hashes run every second across all computers on the network.
In summary
We have now comprehensively covered the following:
- Why cryptographic one way hashing is vital to proof-of-work
- A breakdown of the construction of a Bitcoin block
- The actual mining process and iteration itself
- How nodes can easily validate other blocks
- How the network manages to maintain the algorithm and competitiveness by monitoring the block time and adjusting the target
You should now be able to understand and explain how proof-of-work actually functions and why it is considered to be an entirely secure algorithm that enables decentralization and consensus!
Follow me on Twitter and Medium if you’re interested in more in-depth and informative write-ups like these in the future!
