“In order to understand recursion, one must first understand recursion.”
Recursion can be tough to understand — especially for new programmers. In its simplest form, a recursive function is one that calls itself. Let me try to explain with an example.
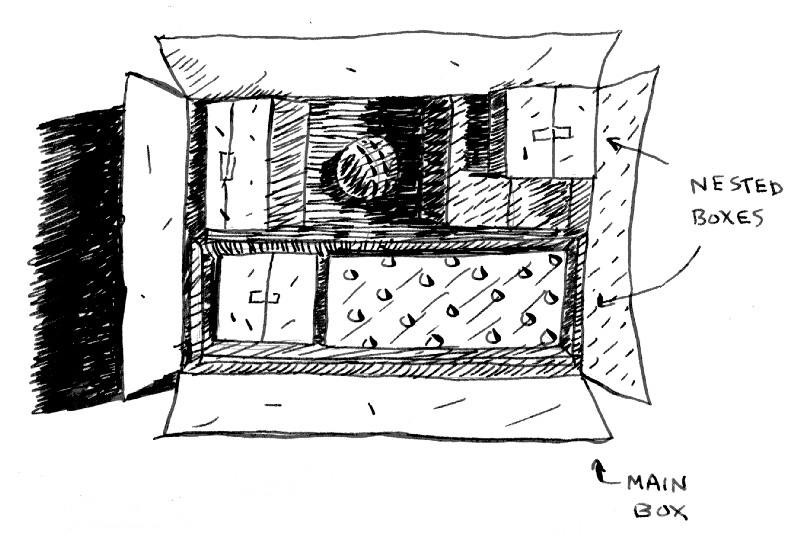
Imagine you go to open your bedroom door and it’s locked. Your three-year-old son pops in from around the corner and lets you know he hid the only key in a box. (“Just like him,” you think.) You're late for work and you really need to get in the room to get your shirt.
You open the box only to find… more boxes. Boxes inside of boxes. And you don’t know which one has the key! You need to get that shirt soon, so you have to think of a good algorithm to find that key.
There are two main approaches to create an algorithm for this problem: iterative and recursive. Here are both approaches as flow charts:
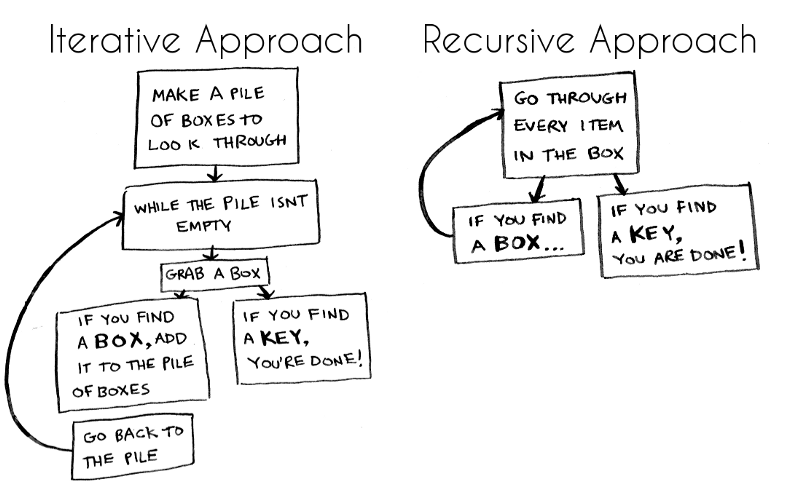
Which approach seems easier to you?
The first approach uses a while loop. While the pile isn’t empty, grab a box and look through it. Here’s some JavaScript-inspired pseudocode that shows what is happening. (Pseudocode is written like code, but meant to be more like human speech.)
function look_for_key(main_box) {
let pile = main_box.make_a_pile_to_look_through();
while (pile is not empty) {
box = pile.grab_a_box();
for (item in box) {
if (item.is_a_box()) {
pile.append(item)
} else if (item.is_a_key()) {
console.log("found the key!")
}
}
}}The second way uses recursion. Remember, recursion is where a function calls itself. Here’s the second way in pseudocode.
function look_for_key(box) {
for (item in box) {
if (item.is_a_box()) {
look_for_key(item);
} else if (item.is_a_key()) {
console.log("found the key!")
}
}
}Both approaches accomplish the same thing. The main purpose for using the recursive approach is that once you understand it, it can be clearer to read. There is actually no performance benefit to using recursion. The iterative approach with loops can sometimes be faster. But mainly the simplicity of recursion is sometimes preferred.
Also, since a lot of algorithms use recursion, it’s important to understand how it works. If recursion still doesn’t seem simple to you, don’t worry: I’m going to go over a few more examples.
Base case and recursive case
Something you have to look out for when writing a recursive function is an infinite loop. This is when the function keeps calling itself… and never stops calling itself!
For instance, you may want to write a count down function. You could write it recursively in JavaScript like this:
// WARNING: This function contains an infinite loop!
function countdown(i) { console.log(i) countdown(i - 1)}
countdown(5); // This is the initial call to the function.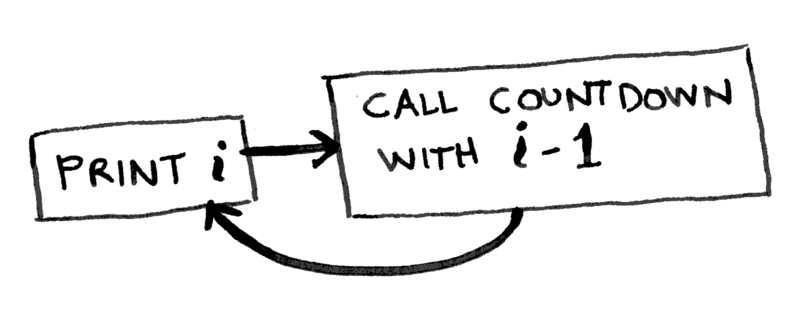
This function will keep counting down forever. If you do accidentally run code with an infinite loop you can press “Ctrl-C” to kill your script. (Or, if you sometimes use CodePen like me, you have to add “?turn_off_js=true” to the end of the URL.)
A recursive function always has to say when to stop repeating itself. There should always be two parts to a recursive function: the recursive case and the base case. The recursive case is when the function calls itself. The base case is when the function stops calling itself. This prevents infinite loops.
Here is the countdown function again, with a base case:
function countdown(i) {
console.log(i) if (i <= 1) { // base case
return;
} else { // recursive case
countdown(i - 1);
}
}
countdown(5); // This is the initial call to the function.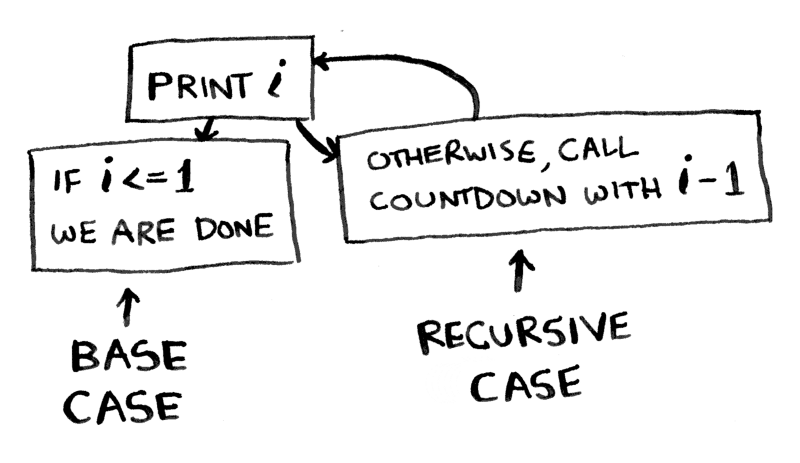
It may not be obvious exactly what is happening in this function. I’ll walk through what happens when you call the countdown function passing in “5”.
We start by printing out the number 5 using console.log. Since five is not less than or equal to zero, we go to the else statement. There we call the countdown function again with the number four (5–1=4 ?).
We log the number 4. Again, i is not less that or equal to zero so we go to the else statement and call countdown with 3. This continues until i equals zero. When that happens, we log the number zero and then i is less than or equal to zero. We finally get to the return statement and pop out of the function.
The Call Stack
Recursive functions use something called “the call stack.” When a program calls a function, that function goes on top of the call stack. This is similar to a stack of books. You add things one at a time. Then, when you are ready to take something off, you always take off the top item.
I will show you the call stack in action with the factorial function. factorial(5) is written as 5! and it is defined like this: 5! = 5 * 4 * 3 * 2 * 1. Here is a recursive function to calculate the factorial of a number:
function fact(x) {
if (x == 1) {
return 1;
} else {
return x * fact(x-1);
}
}Now let’s see what happens if you call fact(3) The illustration bellow shows how the stack changes, line by line. The topmost box in the stack tells you what call to fact you’re currently on.
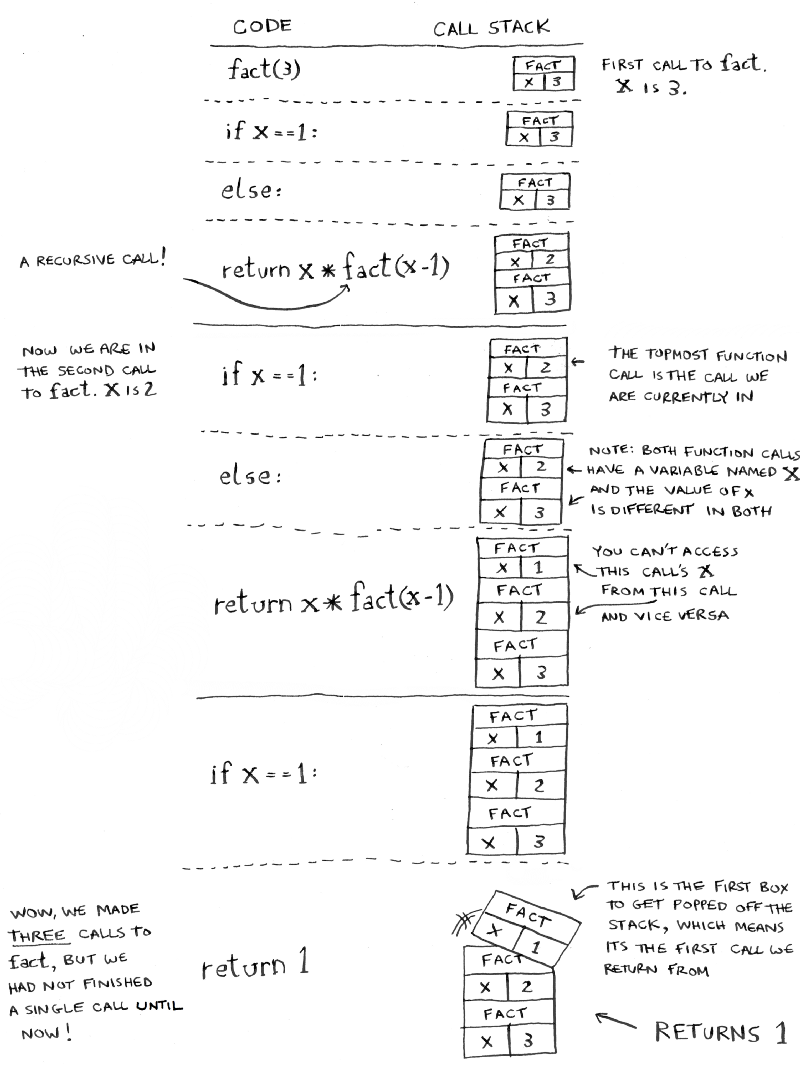
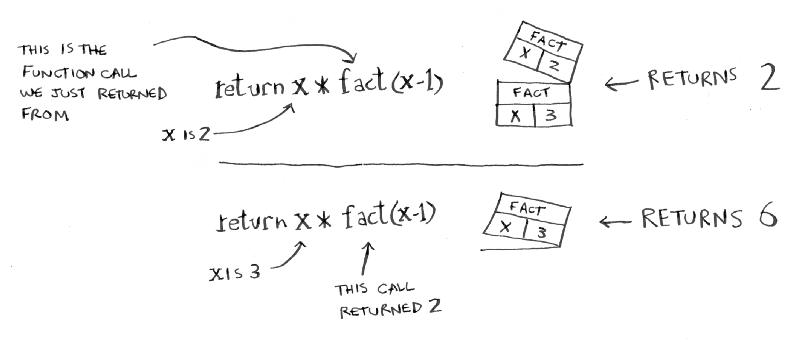
Notice how each call to fact has its own copy of x. This is very important to making recursion work. You can’t access a different function’s copy of x.
Did you find the key yet?
Let’s briefly go back to the original example about looking in nested boxes for a key. Remember, the first method was iterative using loops. With that method, you make a pile of boxes to search through, so you always know what boxes you still need to search.
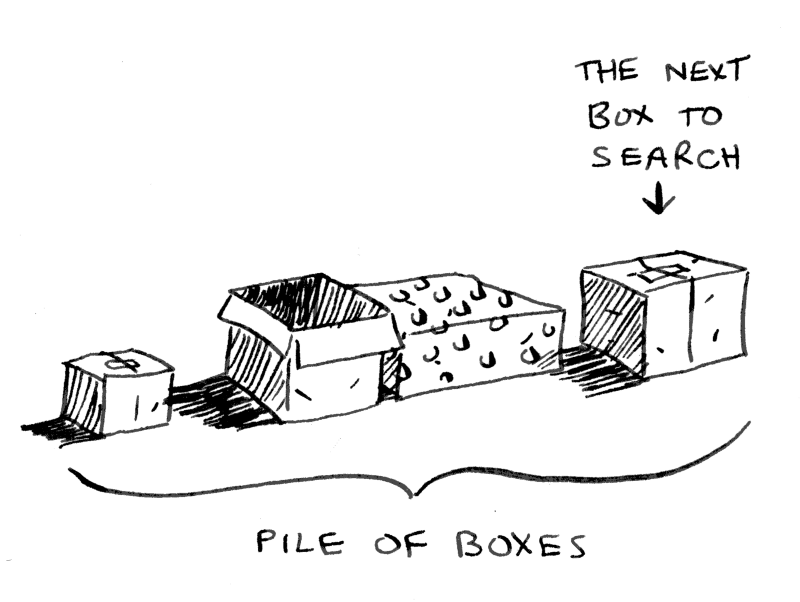
But there is no pile in the recursive approach. How does your algorithm know which boxes you still have to look though? The “pile of boxes” is saved on the stack. This is a stack of half-completed function calls, each with its own half-complete list of boxes to look through. The stack keeps track of the pile of boxes for you!
And thanks to recursion, you can finally find the key and get your shirt!
You can also watch this 5-minute video I made about recursion. It should reinforce these recursion concepts.
Conclusion
I hope this article brought you more clarity about recursion in programming. This article is based on a lesson in my new video course from Manning Publications called Algorithms in Motion. The course (and also this article) is based on the amazing book Grokking Algorithms by Adit Bhargava. He’s the one who drew all the fun illustrations in this article.
If you learn best through books, get the book! If you learn best through videos, consider buying my course.
Get 39% off my course by using code ‘39carnes’!

And finally, to truly understand recursion, you must read this article again. ?
