A code-free guide to Artificial Intelligence
So about a year ago, I read this fantastic article by Trask.
If you didn’t click the link, do it now.
Did you? Ok, good.
Now here’s the thing — The article requires you to know a little bit of python, which you probably do.
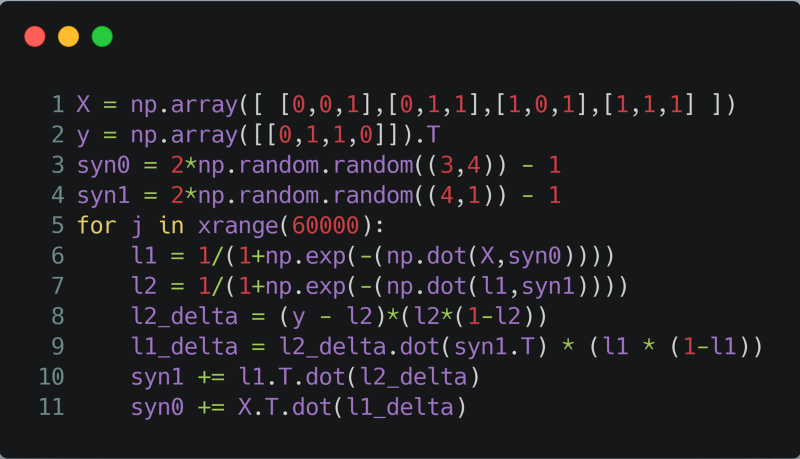
On the off-chance that you’re interested in Neural Networks (if that phrase sounds utterly foreign to you, watch this YouTube playlist) and haven’t learned python yet, congratulations, you’re in the right spot.
But regardless of where you are in the vast landscape of deep learning, I think that once in a while, it’s nice to go back to the basics and revisit the fundamental mathematical ideas that brought us Siri, Alexa, and endless hours of Netflix binge-watching.

So without any further ado, I present to you the three equations that make up what I’ll call the “fundamental theorem of deep learning.”
1. Linear Regression
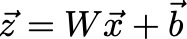
The first equation is pretty basic. I guess the others are as well, but we’ll get to them in due time.
For now, all we’re doing is computing a vector z (from the equation above), where W is a matrix that is initially just filled with a bunch of random numbers, b is a vector that is initially just filled with a bunch of random numbers, and x vector that is not initially filled with a bunch of random numbers.
x is a training example from our dataset. For example, if you’re training a neural net to predict someone’s age given their gender and height, you’d first need a few (or preferably a lot, the more, the merrier) examples of data in the form [[height, gender], age]. The vector [height, gender] is what we’re calling x.
2. Activation Functions
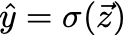
On the left-hand side, we have our predicted values of y, which is the variable that I’m using to denote the labels on our data.
The hat on top means that this value of y is a predicted value, as opposed to the ground truth labels from our dataset.
The z in this equation is the same one that we computed above. The sigma represents the sigmoid activation function, which looks like this:
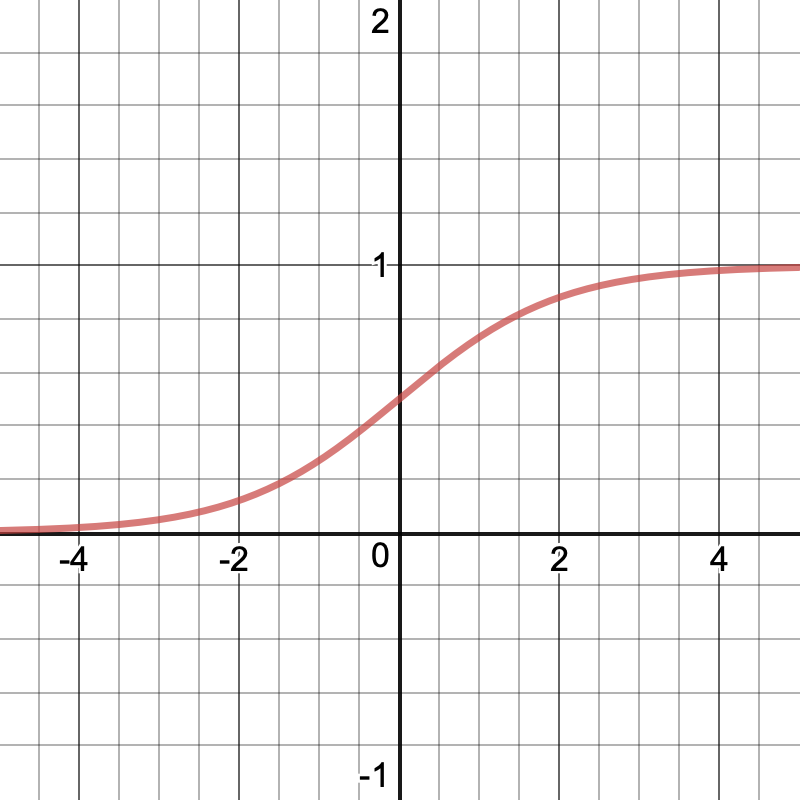
So in plain English, we’re taking z, a vector of real numbers that can be arbitrarily large or small, and squishing its components to be between 0 and 1.
Having a number between 0 and 1 is useful because if we’re trying to build a classifier, let’s say that predicts if an image is a cat or a dog, we can let 1 represent dogs, and we can let 0 be for cats. Or the other way around if you like cats more.

But suppose we’re not doing dogs and cats (yeah right, like there’s any other better use case for machine learning). Let’s go back to our age predictor. Over there, we can’t merely predict 1’s and 0’s.
In general, you could use whatever function you like, not necessarily just a sigmoid. But a bunch of smart people noticed that the sigmoid worked pretty well. So we’re stuck with it.
However, it’s a different story when we’re dealing with labels that are actual numbers, and not classes. For our age predictor, we need to use a different activation function.
Enter ReLU.
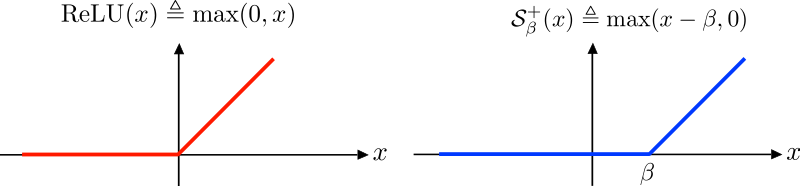
Let me say upfront that I think that this is the most boring part of deep learning. I mean, seriously, just a boring ol’ straightforward-looking function? Where’s the fun in that?
Looks can be deceiving though. While it’s pretty dull — ReLU(x) is just max(0,x) — the ReLU function works really well in practice. So hey, live with it.
3. Back-propagation And Gradient Descent
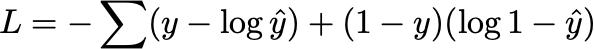
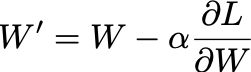
Ok, you got me. I cheated. It’s technically four lines of math. But hey, you could condense steps 1 and 2 into a single step, so I guess I come out victorious.
Now to digest all of that (literal) Greek stuff.
In the first equation, we’re doing that fancy stuff to y and y-hat to compute a single number called the loss, denoted by L.
As can be inferred by the name, the loss measures how badly we’ve lost in our vicious battle to conquer the machine learning grimoire.

In particular, our L here is measuring something called the binary cross entropy loss, which is a shortcut to sounding like you have a math Ph.D. when you’re actually just measuring how far y is from y-hat. Nevertheless, there’s a lot more under the surface of the equation, so check out Daniel Godoy’s article on the topic.
All you need to know to get the intuition behind this stuff is that L gets big if our predicted values are far away from the ground truth values, and L gets tiny when our predictions and reality match.
The sum is there so that we can add up all the messed-up-ness for each of the training examples, so that our neural net understands how messed-up it is overall.
Now, the actual “learning” part of deep learning begins.

The final step in our stack is to update the matrix W and the vector b so that our loss goes down. By doing this, we are effectively minimizing how far are predictions are from the ground truth values, and thus, our model is getting more accurate.
Here’s the equation again:
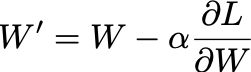
W’ is the matrix with updated numbers that gets us closer to the ground truth. Alpha is a constant that we get to choose. That last term you’re looking at is the gradient of the loss with respect to a parameter. Put simply, it’s a measure of much our loss changes for a small tweak in the numbers in the W matrix.
Again, I’m not going to go too in-depth into gradient descent (the process of updating our numbers in the matrix) since there are already a lot of great resources on the topic. I’d highly recommend this article by Sebastian Ruder.
By the way, we can do the same thing for the initially random values in the b vector. Just tweak them by the right amount in the right direction, and BOOM! We just got closer to an all time low loss.
Conclusion
And there you have it. The three great equations that make up the foundations of the neural networks that we use today.
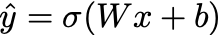
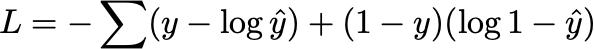
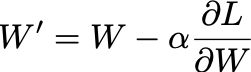
Pause and ponder for a second. What you just saw is a compilation of humanity’s understanding of the intricacies of intelligence.
Sure, this is a pretty basic vanilla neural net that we just looked at, and there have been countless improvements in learning algorithms over the years that have resulted in significant breakthroughs. When coupled with the unprecedented explosion of data and computing power over the years, it seems, to a degree, almost inevitable that well-thought out mathematics is able to grasp the subtle art of distinguishing cats and dogs.
But still. This is where it all began.
In a way, the heart and soul of this decade’s (arguably) most significant technological advancement lie right before your eyes. So take a second. Pause and ponder.

