Previously I wrote about an algorithm for finding out the height of a binary tree using iteration. Though that method gets the job done (in 7 steps no less), the same can be accomplished in a much simpler way.
In my opinion, one of the most powerful programming techniques is recursion. For readers new to programming — it is simply a function or method calling itself. To make the introduction simpler we have a method below that calls another method:
def outer_method(name) (R1)
inner_method + name
end
def inner_method (R2)
"Hello "
end
print outer_method("Steve") -> #"Hello Steve"In the above method outer_method, which takes in a string as argument, calls inner_method, which simply returns the string “Hello “ inside it. Recursion is similar in that, say in this case, outer_method simply calls itself:
def outer_method(name) (R3)
outer_method("hello ") + name
end (R3)One caveat, though, with code R3 above — it will run until the computer complains that resources are not enough to keep processing the method. It’s like running an infinite loop except that infinite loops don’t necessarily raise exceptions. The reason for this is that code R3 doesn’t have a ‘terminal state’ or a point where it doesn’t ‘recurse’ anymore.
We can solve this by including a terminal state:
def outer_method(name) (R4)
return name if name == "hello "
outer_method("hello ") + name
endThe first line inside the method definition simply states that if the argument name is equal to ‘hello’ then simply return name. That will then ignore any line after it. Therefore in the second line, the code outer_method(“hello “) will simply give the string “hello “ to be added to whatever name is in the main argument. So the same print outer_method(“Steve”) will result in the output “hello Steve” as well.
OK then, that may not be the best example for describing recursion (as the recursive version in this case doesn’t have that much advantage over the non-recursive one). But working on the binary tree height problem, we will see that recursion is so much simpler to understand and faster to run.
For this discussion let me put again the same example as I showed in the previous article:
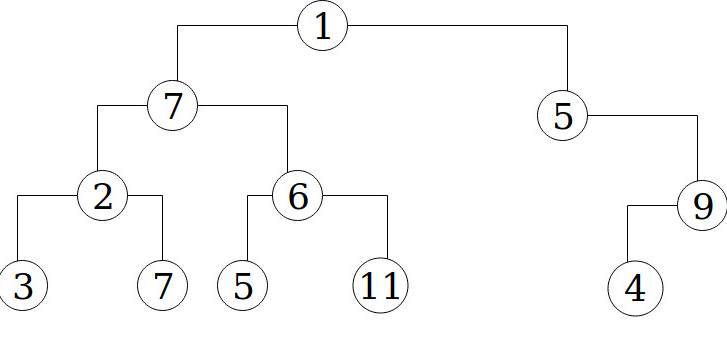
which we can represent as the following array:
tree = [1, 7, 5, 2, 6, 0, 9, 3, 7, 5, 11, 0, 0, 4, 0] (T0)The indices of the left and right children of any sub tree can be determined as follows:
left child of tree[i] is at index 2*i + 1 (T1)
right child of tree[i] is at index 2*i + 2 (T2)If you’re puzzled about how the figure above became the array following it, I’ll direct you to read the previous article on the iterative method for clarification.
And again the formula for calculating the height of a binary tree, as well as the heights of any of its sub trees, is:
height = 1 + max of(left_child_height, right_child_height) (T3)
Now with these we can outline the steps to develop a recursive program.
Step 0: Set default values — To make the initial method call simple, I always like setting default values for the arguments that will change during each recursive call. Since we will repetitively compute heights, our indices will always change.
For instance, to find the height of the root’s (tree[0]) left child we will need to call the method on that left child (whose index is at 2*(0) + 1). Therefore, our method definition will be:
def tree_height_recursive(tree_array,i=0) (S0.1)to indicate that for the initial call we are calling it on the root element. This will simply allow us to call tree_height_recursive by inputting only the tree_array. However, this also means, as we will see in the simulation afterwards, we can find the height of any sub tree by simply including its index as the second argument in the method call.
Step 1: Find terminal state — At which point do we simply return a value and not do any further recursive calls? In our binary tree problem, the terminal state is at:
return 0 if tree[i].nil or tree[i] == 0 (S1.1)It simply says that if the element at index i does not exist or if its value is 0 then simply return 0. Logically, a non-existing sub tree will not have any height.
Step 2: Find the height of the left child — this is where the magic of recursion starts to benefit us. We don’t need any fancy code. No more declaring another array to hold the height of each element. No more multiple variable definitions for height indices and the heights themselves, just:
right_child_height = tree_height_recursive(tree_array, 2*i + 2)
We simply pass the index of the left child as second argument. Can you see why?
We do the same for finding the right child’s height next.
Step 3: Find the height of right child — Likewise, we simply do a recursive call to our method but passing the index of the right child as second argument:
right_child_height = tree_height_recursive(tree_array, 2*i + 2)
Now that we have the heights of the left and right children, we can now compute the total height.
Step 4: Calculate and return total height — As code T3 states, we just add 1 and the height of whichever is taller between the left and right children.
total_height = 1 + [left_child_height, right_child_height].max (S4.1)Since S.4 will be the last statement in our method, then the evaluated total_height will be returned. Remember that if the conditions in S1.1 hold true (our terminal state) then none of Steps 2–4 will run and the method will simply return 0.
The full method below:
Comparing this to the iterative method, the recursive version took 3 fewer steps and 4 fewer variable definitions. The code also (excluding empty spaces and comments) is 7 lines fewer. On top of it, the recursive code will run 2x faster (using the benchmark built-in Ruby module). This is a big advantage if we’re running the method on binary trees hundreds of levels tall.
Now let’s do the same simulation as we did before. For the tree at T0 we run the recursive method:
tree = [1, 7, 5, 2, 6, 0, 9, 3, 7, 5, 11, 0, 0, 4, 0]puts tree_height_recursive(tree_array)-> #should give us 4Note that since we have a default i=0 in our method definition we don’t need to specify the index here because we are finding the height of the whole tree. To make this simulation more intuitive we shall create an imaginary array called call_stack where push every call to tree_height_recursive.
So then when we call the method the first time (the main call), we store it in a temporary variable ht_0 and push it to call_stack:
ht_0 = height of tree[0] = tree_height_recursive(tree_array,i=0)call_stack = [ht_0]We then run Step 1:
tree[0].nil? -> #falsetree[0] == 0 -> #false, it is 2Since this results in false, we go ahead to Step 2:
since i= 0, then 2*i + 1 = 2*0 + 1 = 1:left_child_height = tree_height_recursive(tree_array,1)Since we cannot readily determine this height so then we push it again to call_stack:
ht_1 = left_child_height = tree_height_recursive(tree_array,1)call_stack = [ht_0,ht_1]Then upon doing Step 3:
ht_2 = right_child_height = left_child_height = tree_height_recursive(tree_array,)call_stack = [ht0,ht1,ht2]We cannot proceed to Step 4 until all the items in call_stack have been evaluated by our program and popped off from call_stack (which should happen for every time each height has been evaluated).
So we will also do the same for each of the succeeding heights. For instance, to compute ht1 we know that we have to compute for its own left and right children’s heights too. So that means the method will be called for them too. So as not to prolong this article, the reader is invited to try this on paper.
Ultimately, the method will be called recursively with i = 14 as second argument. Thus, at this point, call_stack will be:
call_stack = [ht0,ht1,ht2,ht3,ht4,ht5,ht6,ht7,ht8,ht9,ht10,ht11,ht12,ht13,ht14]Now we will evaluate each. Note that from tree[7] up to tree[14] the elements don’t have any children. So we can simply evaluate their heights as 1 or 0 (depending on whether tree[i] is 0 or not (where i ≥ 7):
ht14 = 0ht13 = 1ht12 = 0ht11 = 0ht10 = 1ht9 = 1ht8 = 1ht7 = 1Again, when these heights are evaluated we simply pop them off successively from call_stack. After which, call_stack will appear as follows:
call_stack = [ht0, ht1, ht2, ht3, ht4, ht5, ht6]Now, to evaluate ht6 we must remember that it is the call to tree_height_recursive(tree_array, 6). Inside this call we also call on the method to compute for the heights of the left and right children of tree[6]. These we previously already evaluated as ht13 and ht14. So then:
ht6 = 1 + [ht13, ht14].max = 1 + [1,0] = 1 + 1 = 2So we now evaluate ht5, which is the height of tree[5]. We know the heights of its children are ht11 and ht12
ht5 = 1 + [ht11,ht12].max = 1 + [0,0].max = 1 + 0 = 1Doing the same for ht4 to h1 (again the reader is invited to do the confirmation on paper):
ht4 = 1 + [ht9,ht10].max = 1 + [1,1].max = 1 + 1 = 2ht3 = 1 + [ht7, ht8].max = 1 + [1, 1].max = 1 + 1 = 2ht2 = 1 + [ht5, ht6].max = 1 + [1,2].max = 1 + 2 = 3ht1 = 1 + [ht3, ht4].max = 1 + [2,2].max = 1 + 3 = 3Again, we pop out each height from call_stack as we evaluate it so after evaluating ht1 the call_stack appears as follows:
call_stack = [ht0]Now evaluating ht0 is returning to the main call to tree_height_recursive, so this is the remaining Step 4:
ht0 = 1 + [ht1, ht2].max = 1 + [3, 3].max = 1 + 3 = 4ortotal_height = 1 + [left_child_height, right_child_height].maxWhich will return 4 as the result of the main method call.
As I keep mentioning, doing this on paper whether during the algorithm formulation or during simulation will help a lot in understanding it. This same method can also be used to determine the height of any of the sub trees inside the tree_array, for instance to determine only the height of the tree’s left child:
puts tree_height_recursive(tree_array, 1) -> #will print out 3Or any of the lower sub trees:
puts tree_height_recursive(tree_array, 3) -> #will print out 2Wrapping up
The key takeaway in creating a recursive algorithm, in my perspective, is setting the terminal state. Again, this is the scenario wherein the main method will not have to do any recursive call to itself. Without this, the method will just keep calling itself until the computer blows up (hyperbolically speaking…). When we have the terminal state we can easily set the arguments for the recursive calls and know that our method will safely return the value we expect.
Finally, working on algorithms challenge our minds to think. As software engineers, or even engineers in general, our main task is to solve problems. We, therefore, need to develop our critical thinking skills.
If for a problem, our first option is always ‘google it’ and copy/paste other people’s code without fully understanding the problem and the copied solution, then we are defeating ourselves.
So my suggestion is always have pen and paper ready and not immediately type code when faced with an algorithm challenge. Simulate the problem for simple inputs then come up with the code after you determine the steps (like I outlined them above).

