As technology evolves and game contents become more algorithmically generated, it’s not difficult to imagine the creation of a life-like simulation with unique experiences for each player.
Technological breakthroughs, patience, and refined skills will get us there, but the first step is to understand procedural content generation.
Though many out-of-the-box solutions for map generation exist, this tutorial will teach you to make your own two-dimensional dungeon map generator from scratch using JavaScript.
There are many two-dimensional map types, and all have the following characteristics:
1. Accessible and inaccessible areas (tunnels and walls).
2. A connected route the player can navigate.
The algorithm in this tutorial comes from the Random Walk Algorithm, one of the simplest solutions for map generation.
After making a grid-like map of walls, this algorithm starts from a random place on the map. It keeps making tunnels and taking random turns to complete its desired number of tunnels.
To see a demo, open the CodePen project below, click on the map to create a new map, and change the following values:
- Dimensions: the width and height of the map.
- MaxTunnels: the greatest number of turns the algorithm can take while making the map.
- MaxLength: the greatest length of each tunnel the algorithm will choose before making a horizontal or vertical turn.
Note: the larger the maxTurn is compared to the dimensions, the denser the map will be. The larger the maxLength is compared to the dimensions, the more “tunnel-y” it will look.
Next, let’s go through the map generation algorithm to see how it:
- Makes a two dimensional map of walls
- Chooses a random starting point on the map
- While the number of tunnels is not zero
- Chooses a random length from maximum allowed length
- Chooses a random direction to turn to (right, left, up, down)
- Draws a tunnel in that direction while avoiding the edges of the map
- Decrements the number of tunnels and repeats the while loop
- Returns the map with the changes
This loop continues until the number of tunnels is zero.
The Algorithm in Code
Since the map consists of tunnel and wall cells, we could describe it as zeros and ones in a two-dimensional array like the following:
map = [[1,1,1,1,0],
[1,0,0,0,0],
[1,0,1,1,1],
[1,0,0,0,1],
[1,1,1,0,1]]Since every cell is in a two-dimensional array, we can access its value by knowing its row and column such as map [row][column].
Before writing the algorithm, you need a helper function that takes a character and dimension as arguments and returns a two-dimensional array.
createArray(num, dimensions) {
var array = [];
for (var i = 0; i < dimensions; i++) {
array.push([]);
for (var j = 0; j < dimensions; j++) {
array[i].push(num);
}
}
return array;
}
To implement the Random Walk Algorithm, set the dimensions of the map (width and height), themaxTunnels variable, and themaxLength variable.
createMap(){
let dimensions = 5,
maxTunnels = 3,
maxLength = 3;
Next, make a two-dimensional array using the predefined helper function (two dimensional array of ones).
let map = createArray(1, dimensions);Set up a random column and random row to create a random starting point for the first tunnel.
let currentRow = Math.floor(Math.random() * dimensions),
currentColumn = Math.floor(Math.random() * dimensions);To avoid the complexity of diagonal turns, the algorithm needs to specify the horizontal and vertical directions. Every cell sits in a two-dimensional array and could be identified with its row and column. Because of this, the directions could be defined as subtractions from and/or additions to the column and row numbers.
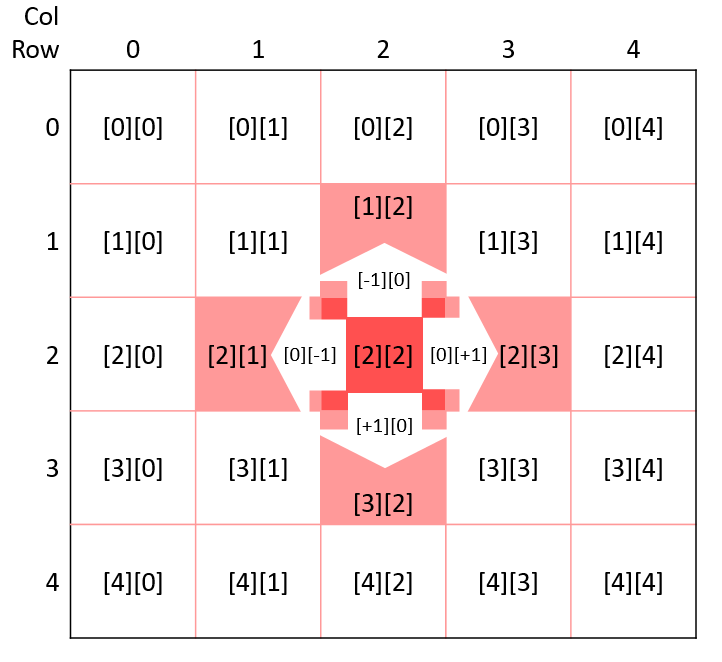
For example, to go to a cell around the cell [2][2], you could perform the following operations:
- to go up, subtract 1 from its row [1][2]
- to go down, add 1 to its row [3][2]
- to go right, add 1 to its column [2][3]
- to go left, subtract 1 from its column [2][1]
The following map illustrates these operations:
Now, set the directions variable to the following values that the algorithm will choose from before creating each tunnel:
let directions = [[-1, 0], [1, 0], [0, -1], [0, 1]];Finally, initiate randomDirection variable to hold a random value from the directions array, and set the lastDirection variable to an empty array which will hold the older randomDirection value.
Note: the lastDirection array is empty on the first loop because there is no older randomDirection value.
let lastDirection = [],
randomDirection;Next, make sure maxTunnel is not zero and the dimensions and maxLengthvalues have been received. Continue finding random directions until you find one that isn’t reverse or identical to lastDirection. This do while loop helps to prevent overwriting the recently-drawn tunnel or drawing two tunnels back-to-back.
For example, if your lastTurn is [0, 1], the do while loop prevents the function from moving forward until randomDirection is set to a value that is not [0, 1] or the opposite [0, -1].
do {
randomDirection = directions[Math.floor(Math.random() * directions.length)];
} while ((randomDirection[0] === -lastDirection[0] &&
randomDirection[1] === -lastDirection[1]) ||
(randomDirection[0] === lastDirection[0] &&
randomDirection[1] === lastDirection[1]));
In the do while loop, there are two main conditions that are divided by an || (OR) sign. The first part of the condition also consists of two conditions. The first one checks if the randomDirection’s first item is the reverse of the lastDirection’s first item. The second one checks if the randomDirection’s second item is the reverse of the lastTurn’s second item.
To illustrate, if the lastDirection is [0,1] and randomDirection is [0,-1], the first part of the condition checks if randomDirection[0] === — lastDirection[0]), which equates to 0 === — 0, and is true.
Then, it checks if (randomDirection[1] === — lastDirection[1]) which equates to (-1 === -1) and is also true. Since both conditions are true, the algorithm goes back to find another randomDirection.
The second part of the condition checks if the first and second values of both arrays are the same.
After choosing a randomDirection that satisfies the conditions, set a variable to randomly choose a length from maxLength. Set tunnelLength variable to zero to server as an iterator.
let randomLength = Math.ceil(Math.random() * maxLength),
tunnelLength = 0;Make a tunnel by turning the value of cells from one to zero while the tunnelLength is smaller than randomLength. If within the loop the tunnel hits the edges of the map, the loop should break.
while (tunnelLength < randomLength) {
if(((currentRow === 0) && (randomDirection[0] === -1))||
((currentColumn === 0) && (randomDirection[1] === -1))||
((currentRow === dimensions — 1) && (randomDirection[0] ===1))||
((currentColumn === dimensions — 1) && (randomDirection[1] === 1)))
{ break; }Else set the current cell of the map to zero using currentRow and currentColumn. Add the values in the randomDirection array by setting currentRow and currentColumn where they need to be in the upcoming iteration of the loop. Now, increment the tunnelLength iterator.
else{
map[currentRow][currentColumn] = 0;
currentRow += randomDirection[0];
currentColumn += randomDirection[1];
tunnelLength++;
}
}
After the loop makes a tunnel or breaks by hitting an edge of the map, check if the tunnel is at least one block long. If so, set the lastDirection to the randomDirection and decrement maxTunnels and go back to make another tunnel with another randomDirection.
if (tunnelLength) {
lastDirection = randomDirection;
maxTunnels--;
}
This IF statement prevents the for loop that hit the edge of the map and did not make a tunnel of at least one cell to decrement the maxTunnel and change the lastDirection. When that happens, the algorithm goes to find another randomDirection to continue.
When it finishes drawing tunnels and maxTunnels is zero, return the resulting map with all its turns and tunnels.
}
return map;
};You can see the complete algorithm in the following snippet:
Congratulations for reading through this tutorial. You are now well-equipped to make your own map generator or improve upon this version. Check out the project on CodePen and on GitHub as a react application.
Thanks for reading! If you liked this story, don't forget to share it on social media.
Special thanks to Tom for co-writing this article.

