by David Mack
How to pick the best learning rate for your machine learning project

A common problem we all face when working on deep learning projects is choosing a learning rate and optimizer (the hyper-parameters). If you’re like me, you find yourself guessing an optimizer and learning rate, then checking if they work (and we’re not alone).
To better understand the affect of optimizer and learning rate choice, I trained the same model 500 times. The results show that the right hyper-parameters are crucial to training success, yet can be hard to find.
In this article, I’ll discuss solutions to this problem using automated methods to choose optimal hyper-parameters.
Experimental setup
I trained the basic convolutional neural network from TensorFlow’s tutorial series, which learns to recognize MNIST digits. This is a reasonably small network, with two convolutional layers and two dense layers, a total of roughly 3,400 weights to train. The same random seed is used for each training.
It should be noted that the results below are for one specific model and dataset. The ideal hyper-parameters for other models and datasets will differ.
(If you’d like to donate some GPU time to run a larger version of this experiment on CIFAR-10, please get in touch).
Which learning rate works best?
The first thing we’ll explore is how learning rate affects model training. In each run, the same model is trained from scratch, varying only the optimizer and learning rate.
The model was trained with 6 different optimizers: Gradient Descent, Adam, Adagrad, Adadelta, RMS Prop, and Momentum. For each optimizer, it was trained with 48 different learning rates, from 0.000001 to 100 at logarithmic intervals.
In each run, the network is trained until it achieves at least 97% train accuracy. The maximum time allowed was 120 seconds. The experiments were run on an Nvidia Tesla K80, hosted by FloydHub. The source code is available for download.
Here is the training time for each choice of learning rate and optimizer:
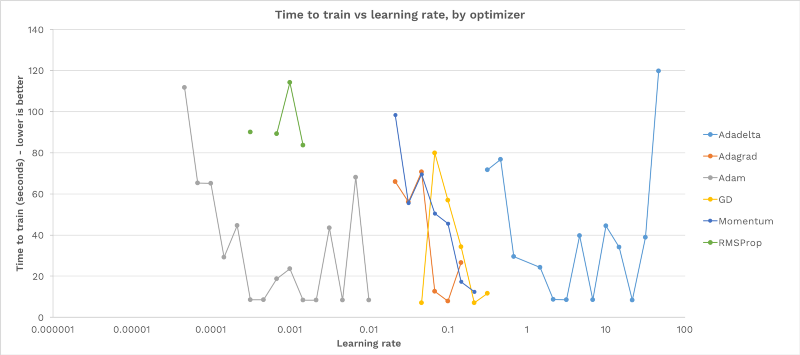
The above graph is interesting. We can see that:
- For every optimizer, the majority of learning rates fail to train the model.
- There is a valley shape for each optimizer: too low a learning rate never progresses, and too high a learning rate causes instability and never converges. In between, there is a band of “just right” learning rates that successfully train.
- There is no learning rate that works for all optimizers.
- Learning rate can affect training time by an order of magnitude.
To summarize the above, it’s crucial that you choose the correct learning rate. Otherwise your network will either fail to train, or take much longer to converge.
To illustrate how each optimizer differs in its optimal learning rate, here is the the fastest and slowest model to train for each learning rate, across all optimizers. Notice that the maximum time is 120s (for example, network failed to train) across the whole graph — there is no single learning rate that works for every optimizer:
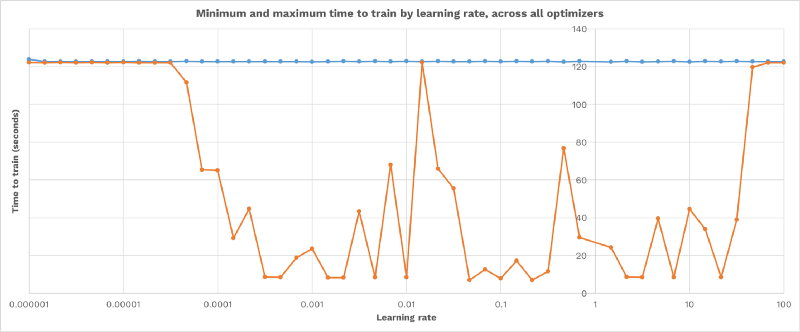
Check out the wide range of learning rates (from 0.001 to 30) that achieve success with at least one optimizer from the above graph.
Which optimizer performs best?
Now that we’ve identified the best learning rates for each optimizer, let’s compare the performance of each optimizer training with the best learning rate found for it in the previous section.
Here is the validation accuracy of each optimizer over time. This lets us observe how quickly, accurately, and stably each performs:
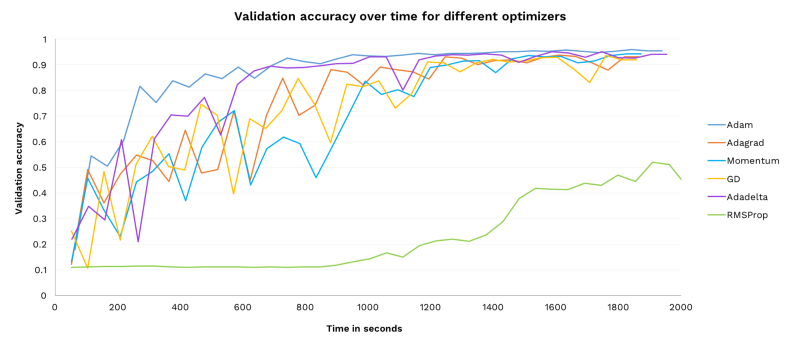
A few observations:
- All of the optimizers, apart from RMSProp (see final point), manage to converge in a reasonable time.
- Adam learns the fastest.
- Adam is more stable than the other optimizers, and it doesn’t suffer any major decreases in accuracy.
- RMSProp was run with the default arguments from TensorFlow (decay rate 0.9, epsilon 1e-10, momentum 0.0) and it could be the case that these do not work well for this task. This is a good use case for automated hyper-parameter search (see the last section for more about that).
Adam also had a relatively wide range of successful learning rates in the previous experiment. Overall, Adam is the best choice of our six optimizers for this model and dataset.
How does model size affect training time?
Now lets look at how the size of the model affects how it trains.
We’ll vary the model size by a linear factor. That factor will linearly scale the number of convolutional filters and the width of the first dense layer, thus approximately linearly scaling the total number of weights in the model.
There are two aspects we’ll investigate:
- How does the training time change as the model grows, for a fixed optimizer and training rate?
- Which learning rate trains fastest on each size of model, for a fixed optimizer?
How does training time change as the model grows?
Below shows the time taken to achieve 96% training accuracy on the model, increasing its size from 1x to 10x. We’ve used one of our most successful hyper-parameters from earlier:
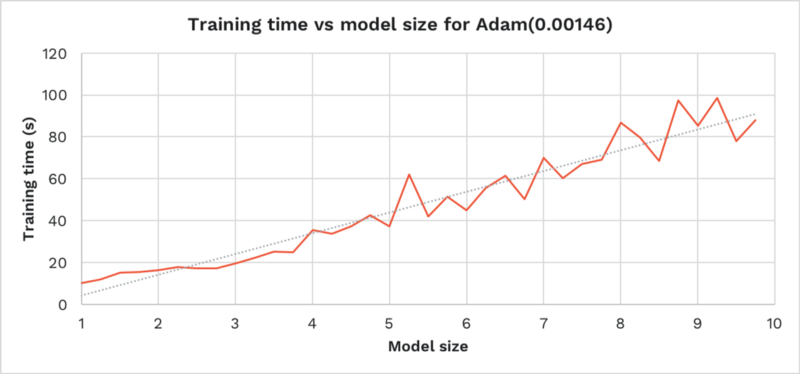
- The time to train grows linearly with the model size.
- The same learning rate successfully trains the network across all model sizes.
(Note: the following results can only be relied upon for the dataset and models tested here, but could be worth testing for your experiments.)
This is a nice result. Our choice of hyper-parameters was not invalidated by linearly scaling the model. This may hint that hyper-parameter search can be performed on a scaled-down version of a network, to save on computation time.
This also shows that, as the network gets bigger, it doesn’t incur any O(n²) work in converging the model (the linear growth in time can be explained by the extra operations incurred for each weight’s training).
This result is further reassuring, as it shows our deep learning framework (here TensorFlow) scales efficiently.
Which learning rate performs best for different sizes of model?
Let’s run the same experiment for multiple learning rates and see how training time responds to model size:
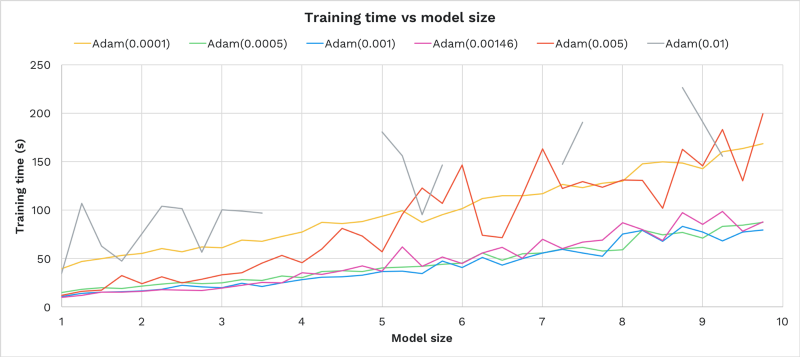
- Learning rates 0.0005, 0.001, 0.00146 performed best — these also performed best in the first experiment. We see here the same “sweet spot” band as in the first experiment.
- Each learning rate’s time to train grows linearly with model size.
- Learning rate performance did not depend on model size. The same rates that performed best for 1x size performed best for 10x size.
- Above 0.001, increasing the learning rate increased the time to train and also increased the variance in training time (as compared to a linear function of model size).
- Time to train can roughly be modeled as c + kn for a model with n weights, fixed cost c and learning constant k=f(learning rate).
In summary, the best performing learning rate for size 1x was also the best learning rate for size 10x.
Automating choice of learning rate
As the earlier results show, it’s crucial for model training to have an good choice of optimizer and learning rate.
Manually choosing these hyper-parameters is time-consuming and error-prone. As your model changes, the previous choice of hyper-parameters may no longer be ideal. It is impractical to continually perform new searches by hand.
There are a number of ways to automatically pick hyper-parameters. I’ll outline a couple of different approaches here.
Grid search
Grid search is what we performed in the first experiment — for each hyper-parameter, create a list of possible values. Then for each combination of possible hyper-parameter values, train the network and measure how it performs. The best hyper-parameters are those that give the best observed performance.
Grid search is very easy to implement and understand. It’s also easy to verify that you’ve searched a sufficiently broad section of the parameter search. It’s very popular in research because of these reasons.
Population-based training
Population-based training (DeepMind) is an elegant implementation of using a genetic algorithm for hyper-parameter choice.
In PBT, a population of models are created. They are all continuously trained in parallel. When any member of the population has had sufficiently long to train to show improvement, its validation accuracy is compared to the rest of the population. If its performance is in the lowest 20%, then it copies and mutates the hyper-parameters and variables of one of the top 20% performers.
In this way, the most successful hyper-parameters spawn many slightly mutated variants of themselves and the best hyper-parameters are likely discovered.
Next steps
Thanks for reading this investigation into learning rates. I began these experiments out of my own curiosity and frustration around hyper-parameter turning, and I hope you enjoy the results and conclusions as much as I have.
If there is a particular topic or extension you’re interested in seeing, let me know. Also, if you’re interested in donating some GPU time to run a much bigger version of this experiment, I’d love to talk.
These writings are part of a year-long exploration of AI architecture topics. Follow this publication (and give this article some applause!) to get updates when the next pieces come out.
