How to Sort a List Recursively in Python

When you want to sort a list or array in Python, there are many sorting algorithms you can use.

Some use looping concepts like Insertion Sort, Bubble Sort, and Selection Sort. On the other hand, you can also sort the same list or array using Merge Sort with the help of recursion.

In this article, you will learn how the Merge Sort algorithm works. You will also learn how recursion plays an important role in Merge Sort.

How Recursion Works

As a prerequisite, we will first understand how recursion works, as it's the backbone of the merge sort algorithm.

First, you should know that a recursive function is one that calls itself until it reaches its desired outcome.

Now, unless you set some condition to stop this process, it'll go on forever – or until your JS code throws an error. This is known as a base case, and it will stop the function from calling itself when its condition is met.

Now that you know the basics of recursion, let's get into the weeds a bit and understand how it works under the hood:

In general, recursion works based on a concept called Principal Mathematical Induction (PMI). In simple words, PMI is a technique which is used to prove certain statements from a basic set of proven statements.

Usually, there are three steps in this process.

Let's prove that the formula of n natural number is P(n)= n*(n+1)/2 using PMI:

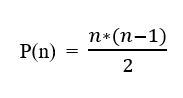
Step 1: The first step is also known as the base case. During this step, you specify the proven statements. Universally, we know that the sum of the first 1 natural number is 1. Let's consider it the left-hand side of the equation (LHS).

When we apply n = 1 in the the formula, we get p(1) = 1*(1+1)/2 => 1 as the right-hand side (RHS).

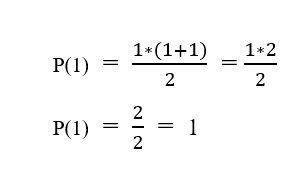
This means that LHS = RHS. This step confirms it's a valid base case.

Step 2: This step is known as the Induction Hypothesis. In this step, we simply assume that this formula is true for some integer k where 1 < k < n. So, we substitute k in the formula and we get p(k) = k*(k+1)/2:

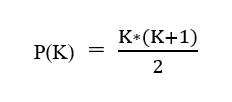
Step 3: This step is known as the Induction Step. At this point, we have to prove that this will work for the integer k+1.

When we substitute k + 1 in the formula and consider it as the LHS, then we get the following:

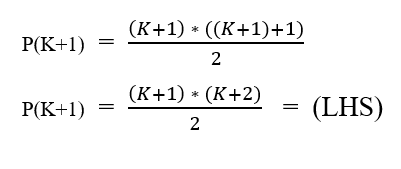
For the RHS, we know that the sum of the natural number k+1 integer is equal to the sum of the natural number of k integer and k+1th integer. We can write it like this:

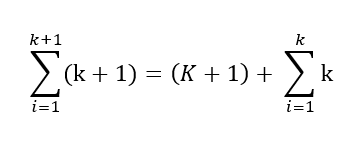
The above equation can be rewritten like this:

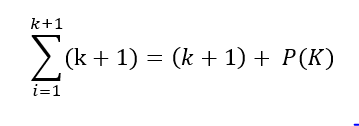
At this point, we know the value of p(k) from step-2 (Induction Hypothesis). When we substitute the value of p(k), we get this:

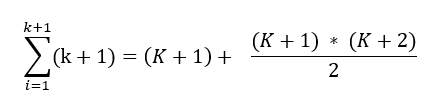
We can take the common denominator and simplify the equation, and we get:

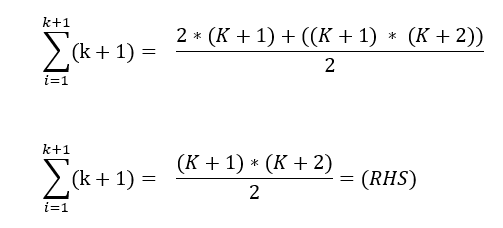
On comparing the LHS and RHS, we get the same result and we have proved that this formula works for k+1 integers.

Also, when we substitute n in the place of k+1, we get the end result as:

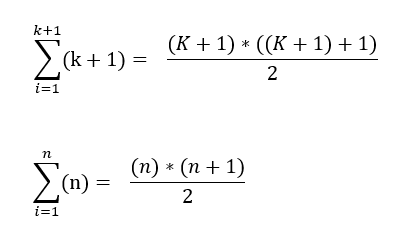
We have proven that formula for n natural number is n*(n+1)/2.

When we observe all the steps in PMI, we did a simple assumption at step-2 and and therefore, we proved the statement at step-3.

This is how recursion works: we initialize a base case for a problem at the start of the function and we assume that this function works for small values of the same problem. Then as the final step, we prove that this works for the existing problem.

How the Merge Sort Algorithm Works

The Merge Sort algorithm works by breaking down an unsorted list into two halves. You then call the merge sort on each of these two parts.

Since, we know recursion works based on Principal Mathematical Induction (PMI), we assume that the smaller lists gets sorted on calling merge sort on these 2 smaller lists.

Note: Before calling recursion in smaller lists, it's more important to define a base case for the function as it acts as a stopping point for the recursive call.

Here, the base case for the merge sort will be if the length of the list is 1. In that case (if the length is 1, it means there's only one item in the list), the list is already sorted so we have to just return the list as it is.

For more clarity, let's take an example and implement merge sort over the unsorted list.

my_list = [3,8,2,7,1,4,5] 

In the code above, you can see that the variable my_list contains a list which is unsorted.

Now, since the length of my_list is not 1, we can't assume that it is sorted. So, we call merge sort on first half list1 = [3,8,2] and also call merge sort on second half list2 = [7,1,4,5].

We assume that list1 and list2 are sorted as per the induction step. Now, the list looks like list1 = [2,3,8] and list2 = [1,4,5,7]. Now, all we have to do is just merge those two sorted lists into one using the two pointer technique.

In order to combine and sort the two smaller sorted lists, we take 2 pointers, pointing at the start of each list.

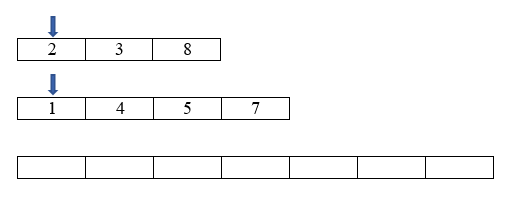
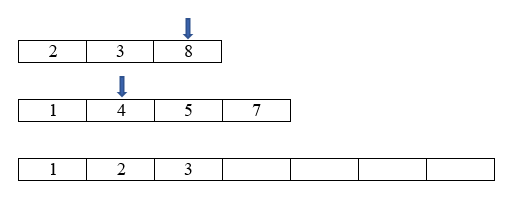
We are comparing the value at each place the pointer points, and whichever is smaller we append that value next in the final list. Then we move the pointer place to the next index.

After looping through this process, when we reach the first final index (in one of the two loops we're joining) we stop the loop. Then we append all the values in the other list (if any remain) to the final list.

Using this technique, we can merge and sort the two small pre-sorted lists.

When we're using recursion, we assume that it works when we call the same function for a smaller problem. This assumption comes from the induction hypothesis step in PMI.

So when we declare the base case for the problem, we similarly assume that the function will return the correct answer for smaller problems. All we have to do is prove that this works for larger problems, too.

In this algorithm, we declared that the base case is that for a list length of 1, the list is sorted. In the induction hypothesis step, we assumed that algorithm would work for half of the list. In the third step, we just merged the sorted list and proved that this will work on a larger list.

Python Code for the Merge Sort Algorithm

def merge_sort(my_list):

	# Base Case
    if len(my_list) <= 1:
        return my_list
   
    list_1 = my_list[0:len(my_list) // 2]
    list_2 = my_list[len(my_list) // 2:]
    
   	# Induction Step
    ans_1 = merge_sort(list_1)
    ans_2 = merge_sort(list_2)
    
    # Sorting and merging two sorted list
    sort_list = sort_two_list(ans_1, ans_2)
    return sort_list



# Separate Function to sort and merge 2 sorted lists
def sort_two_list(list_1, list_2):
    final_list = []
    i = 0
    j = 0
    while i < len(list_1) and j < len(list_2):
        if list_1[i] <= list_2[j]:
            final_list.append(list_1[i])
            i += 1
            continue
        final_list.append(list_2[j])
        j += 1

    while i < len(list_1):
        final_list.append(list_1[i])
        i = i + 1
        
    while j < len(list_2):
        final_list.append(list_2[j])
        j = j + 1
        
    return final_list


my_list = [3, 8, 2, 7, 1, 4, 5]
ans = merge_sort(my_list)
print(ans)
# prints [1, 2, 3, 4, 5, 7, 8]

As you see in the above code, I have implemented two separate functions for sorting and merging the two sorted lists. This leads to better readability and easier code reviews.

The main drawback in merge sort is it uses more space. This is because, at every recursive call, a new list gets created and recursion is called on that new list. So space complexity for the worst case scenario is O(n) and time complexity is O(n log n).

Conclusion

Merge Sort is pretty quick in sorting a list recursively from a time complexity perspective. This is useful for counting inversions in lists and it's widely used for external sorting applications than other sorting algorithms.

Happy programming...