Data structures play a vital role in computer science. They are essential for designing efficient software infrastructure.
Simply put, a data structure is a way of organizing and storing data in a computer so that it can be accessed and manipulated reliably. Also, it provides a set of operations such as inserting, deleting, or searching, with their respective computational costs.
Why Are Data Structures Useful?
The value of data structures lies in their ability to approach complex problems in a simpler and more comprehensive way. As they allow for the storage and retrieval of large amounts of data, they become especially important in today's world. Data is being generated at an unprecedented rate. And that data is later processed to extract valuable insights with the goal of developing new products and services that make our lives easier.
Another one of the main advantages of data structures is their ability to reduce the time complexity of certain algorithms. By using the appropriate data structure, you can perform operations such as searching, sorting, and inserting data in sub-linear time.
For example, using a Hash Table instead of a Linked List to store data enables us to access any element of the structure in constant time, reducing the complexity from O(n) to O(1).
In this context, one of the most important aspects of data structures is their ability to organize data in a way that allows for efficient memory usage and reduces the time required to perform specific tasks.
Choosing the right data structure for a large-scale problem is a critical decision that can greatly impact the performance of an algorithm or software application. They also serve as the foundation for many core computer science concepts, such as algorithms, databases, and compilers.
So, in order to fully grasp their significance, you need to understand their inner workings and analyze their strengths and weaknesses.
Different Types of Data Structures
There are numerous types of data structures, including the previously mentioned linked lists, arrays, stacks, queues, trees, and graphs. And each has its own set of use cases and benefits.
What is a Trie Data Structure?
One particularly interesting data structure we will focus on in this article is the Trie, a tree-like data structure employed to store a dynamic set or associative array where the keys are typically strings.
Commonly, we use tries in tasks such as searching and auto-completion, where a large dataset of strings needs to be efficiently stored, checked, or searched.
The Trie is particularly efficient for tasks that involve searching through a large set of strings, as it can perform these tasks with a time complexity of O(m), where m is the length of the searched string. This makes the Trie an attractive choice for applications such as dictionaries, autocomplete features, and IP routing tables.
Despite the numerous advantages offered by Tries, one of the main challenges associated with their implementation is their potential complexity, particularly in their instantiation and visualization.
The visualization of data structures is an essential aspect of understanding their basis and evaluating their performance. But visualizing Tries can become increasingly difficult as the number of nodes and branches grows.
This can lead to confusion and misunderstandings, making it harder for developers and researchers to comprehensively understand the Trie's behavior and throughput. For this reason, this article shows you how to automate the visualization of Trie data structures.
Benefits of Automating the Visualization Process
By automating the visualization process, we unlock a multitude of advantages that can positively impact the overall software development process, transcending the boundaries of traditional visualization techniques.
First and foremost, automation brings with it the gift of efficiency. By eliminating the need for manual visualization and enabling the instantaneous generation of visual representations, we drastically reduce the time spent on creating and understanding Trie diagrams.
This newfound efficiency frees up valuable time for other tasks, allowing us to focus on optimizing and tackling major abstract challenges, ultimately driving progress in the field.
In addition, automation paves the way for consistency and accuracy in visualizing Tries. The human element is prone to errors, leading to misunderstandings and misinterpretations of the underlying data structure. Automating the visualization process removes these potential pitfalls, ensuring that the visual representations generated are trustworthy, precise, and true to the data structure.
Also, automation empowers scalability, enabling the visualization of even the most complex and large-scale datasets. As the size of a Trie increases, so does the difficulty of manual visualization. Automation sidesteps this issue by generating visual representations regardless of the complexity or size of the Trie. This grants researchers and developers an unprecedented level of insight into their systems.
Lastly, automation fosters accessibility and inclusivity in the world of data structure visualization.
Traditionally, creating and interpreting visualizations required a certain level of expertise and experience. But by automating this process, we democratize access to the benefits of visualization. This makes it possible for individuals with varying levels of expertise to analyze and understand Trie data structures.
This, in turn, can inspire collaboration and innovation across a wide range of disciplines and industries.
Here's what we'll cover in this guide:
- What is a Trie?
- Main Components of a Trie Data Structure
- Operations You Can Perform on a Trie
- How to Implement a Trie
- How to Visualize a Trie
What is a Trie?
A Trie is a unique and powerful data structure in computer science. It's used to store and manipulate associative arrays or dynamic sets where the keys are typically strings. It is also known as a prefix, radix, or digital tree.
Originating from the term "retrieval," the Trie is a tree-like structure that efficiently organizes and searches through large sets of strings based on their prefixes. This makes it an ideal choice for applications such as dictionaries or spell-checking features.
The Trie comprises nodes connected by branches, each one representing a single character in a string. The root node is usually empty or holds a special value, while the leaf nodes signify the end of a string.
As we traverse from the root node to a leaf node, we construct the string by concatenating the characters represented by each node.
Advantages of the Trie Data Structure
Unlike other tree data structures like binary search trees, Tries don't store the actual keys associated with the nodes. Instead, the position of a node within the Trie structure defines the key.
One of the main advantages of Tries compared to other alternatives like BSTs (Binary Search Trees) is their ability to perform search, insert, and delete operations with a time complexity of O(m). In this case, m is the length of the key (word) being searched, inserted, or deleted.
This is particularly efficient when working with large datasets, as the complexity is independent of the number of keys stored in the Trie. In other words, the performance of these operations does not degrade as the Trie grows in size.
Tries have several other notable features, including:
- Prefix sharing: A Trie stores strings by sharing their common prefixes, reducing memory usage and providing a compact dataset representation. This feature is particularly beneficial when working with large sets of strings that share many common prefixes.
- Alphabet-independent size: The size of a Trie is not dependent on the size of the alphabet of the words it contains, making it well-suited for a wide range of applications and datasets.
- Support for advanced search operations: Tries can perform advanced search operations, such as prefix matching, autocomplete suggestions, and approximate string matching, which are difficult or inefficient to implement using other data structures.
- Space optimization with compressed Tries: Variations of the Trie data structure, such as Radix Tries, can further optimize memory usage by collapsing multiple nodes with single child nodes into a single node, resulting in a more compact structure.
Still, Tries are not without their drawbacks. One primary concern is their potential space inefficiency. Tries can consume a considerable amount of memory, particularly when working with large alphabets or datasets with few shared prefixes. This issue can be mitigated to some extent through compression techniques and alternative Trie implementations.
In summary, when deciding whether or not to use a Trie, you should consider the specific requirements of your application carefully, the nature of your dataset, and the trade-offs between performance, memory usage, and complexity.
Main Components of a Trie Data Structure
A Trie consists of several fundamental components that work together to compose its basis. Understanding these elements is crucial for solidly comprehending Tries and their full potential.
Here, we will discuss the main parts of a trie, some of them previously mentioned:
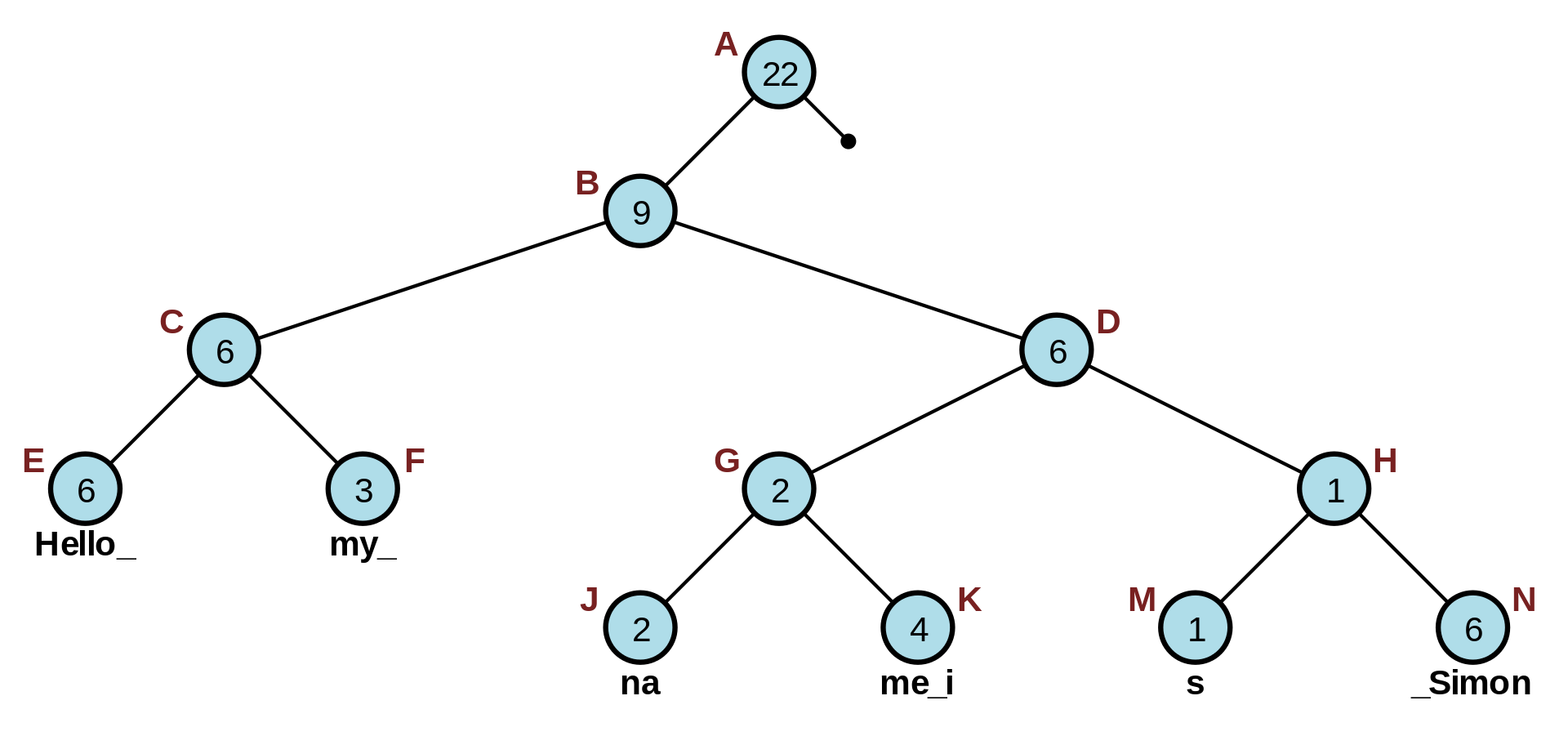
- Nodes: A Trie consists of nodes, each representing a single character in a string. Every Trie has a root node, above colored in red, which is typically empty or holds a special value. The other nodes in the Trie correspond to individual characters of the stored strings.
- Edges: Edges, or branches, connect the nodes in a Trie. Each edge links a parent node to a child node and represents a transition between two characters in a string. The edges help form the paths from the root node to the leaf nodes, which correspond to complete strings.
- Leaf Nodes: Leaf nodes (colored in green) are the terminal nodes, signifying the end of a string. Depending on the specific application, they may contain additional information, such as the string's frequency, value, or associated data.
- Pointers: Each node in a Trie typically contains an array or set of pointers, one for each possible character in the alphabet. These pointers reference the child nodes corresponding to a string's next character. If a pointer is null or is not contained in the set, it indicates that there is no child node for that character.
- Common Prefixes: One of Trie's defining characteristics is its ability to share common prefixes among stored strings. This feature (optional depending on the applied problem) provides support when performing prefix-based operations and searches.
- End-of-Word Flag: A marker or end flag is often used to differentiate between complete strings and prefixes. This boolean value is set in a node to indicate that the path from the root node to that node represents a complete string in the Trie.
Operations You Can Perform on a Trie
Now that you've seen the fundamental elements of a Trie, you have a broad idea about their underlying operations. You also understand the trie's value as a data structure.
At this point, you should try to understand technically the complexity of each operation that can be performed on them.
How to Insert a String into a Trie
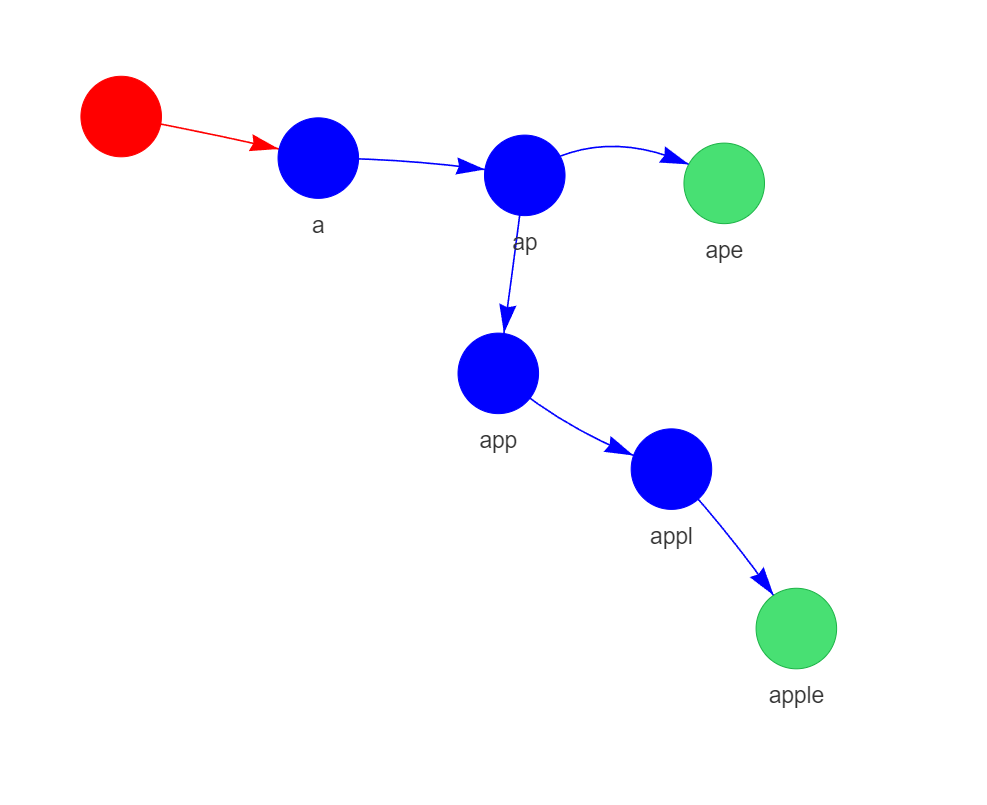
Imagine the Trie as a tree with many branches, starting from a root node. To insert a string, begin at the root and follow these steps:
- For each character in the string, check if there's an edge (branch) corresponding to the character.
- If there is, move to the child node connected by the edge.
- If not, create a new node for the character, connect it to the current node with an edge, and move to the new node.
- Once you reach the end of the string, mark the final node as the end of a word.
Example: Insert "apple" and "ape" into an empty Trie
How to Search for a String in a Trie
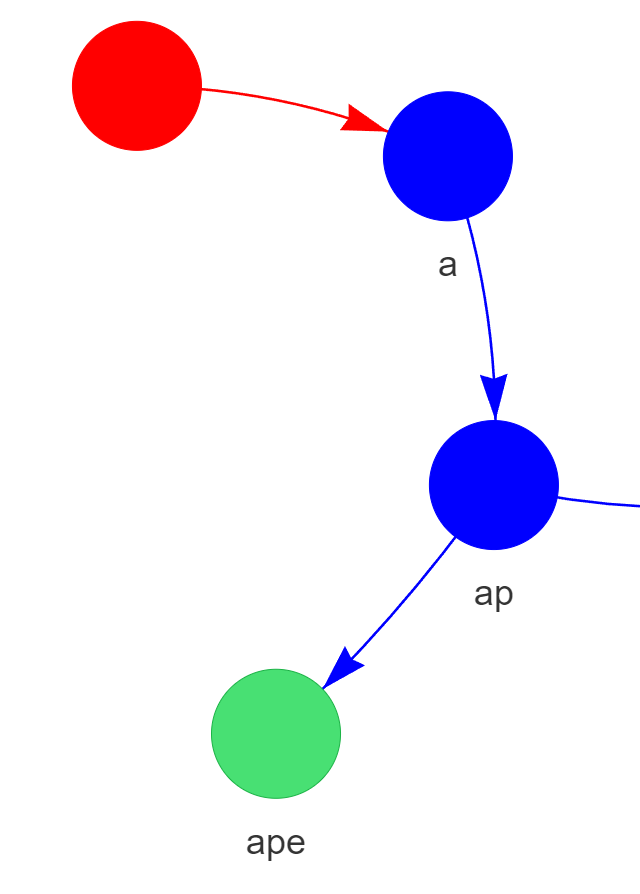
To search for a string in a Trie, start at the root and follow these steps:
- For each character in the string, check if there's an edge corresponding to the character.
- If there is, move to the child node connected by the edge.
- If there isn't, the string is not in the Trie, and the search fails.
- If you reach the end of the string, check if the final node is marked as the end of a word. If it is, the search is successful.
Example: Search for "ape" in the Trie containing "apple" and "ape"
How to Delete a String from a Trie
To delete a string from a Trie, start at the root and follow this process:
- Search for the string, keeping track of the nodes and edges traversed.
- If the string is not found, the deletion fails.
- Remove the end flag from the final node if the string is found.
- Starting from the final node, move back toward the root, deleting nodes and edges that don't have other children or don't belong to other complete words.
Example: Delete "ape" from the Trie containing "apple" and "ape"

By thinking about these operations as traversals through the Trie's branches, we can then more easily account for the memory and time complexity of each one. They are equivalent to tree (or linked list) traversal tasks.
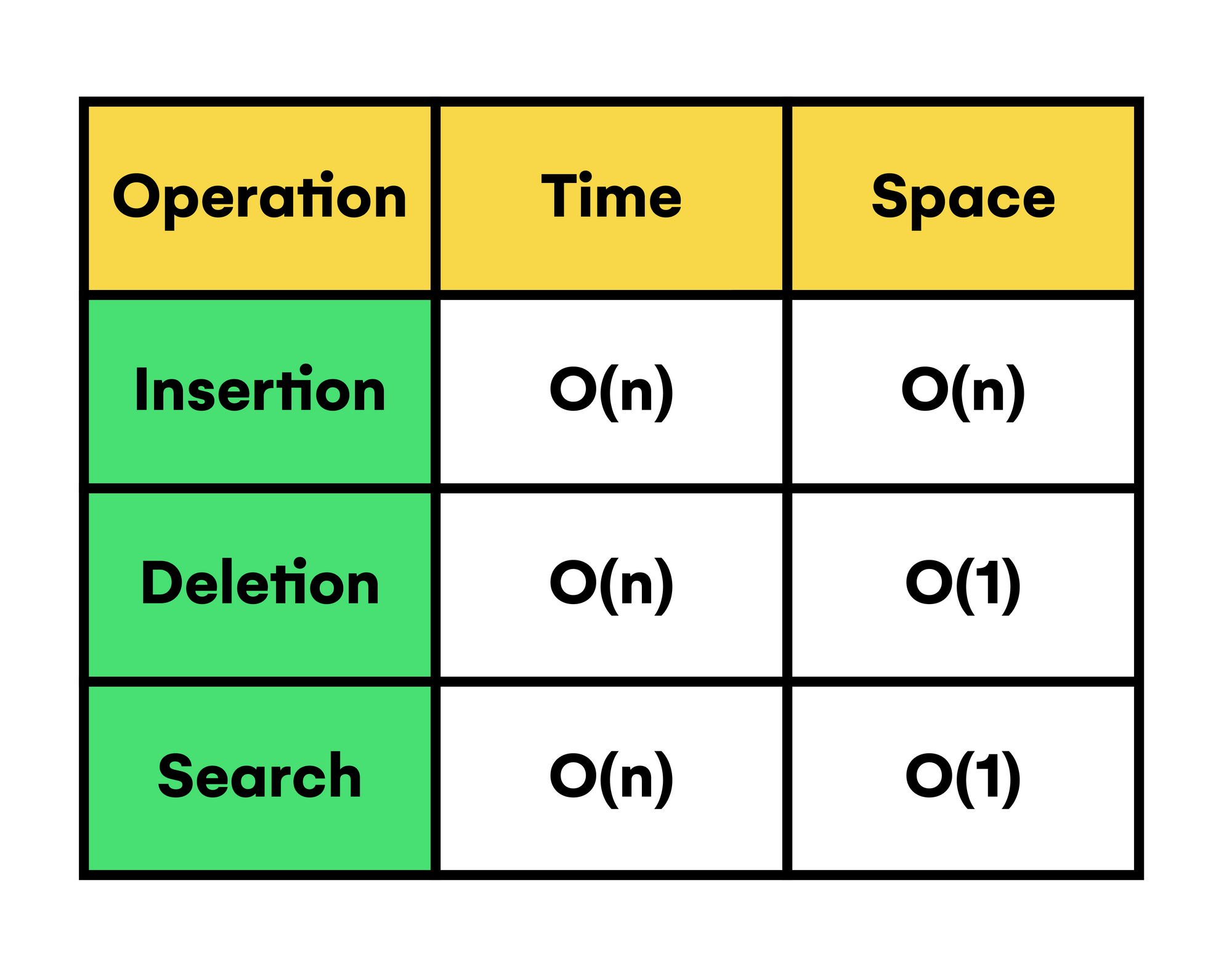
As seen in the table, all the operations have the same linear time complexity (being n the length of the word being processed). This means that they only require performing a single traversal across the word's characters to achieve the desired result.
But in terms of space, deletion and search don't need additional memory. This means that they have a constant complexity.
Finally, it is worth pointing out that the worst-case time complexity of the deletion operation could be in the order of O(2n), having to traverse through the branch where the word to be deleted resides once more in order to remove possible unused nodes in the Trie.
How to Implement a Trie
Now we will use Python to implement a Trie specifically designed for a validation problem (but you can tailor it for any given application).
The sample problem our implementation will solve is the following: given a board with NxN squares, we want a user to be able to introduce the coordinates of a specific square using a text message in order to select and operate with it.
For this purpose, the input will consist of a series of alphabetical characters to refer to the board's vertical axis, followed by another set of numerical characters to select the remaining axis.

In this case, we can use regular expressions or similar techniques to validate if the user's input matches the required structure and format. But if we don't mind our program consuming more memory, we have the alternative of using a Trie.
This choice may, at first glance, seem overly inefficient in terms of memory since we must create and use a specific data structure that consumes space during the entire execution of the program.
But using a Trie provides a constant validation time for all possible inputs, and since in this example the coordinates are short length strings, storing them in memory proves to be reasonable.
Note that in this example, the Trie search operation (validation) runs in "constant" time due to the fixed length of all its words. That is, as the board won't scale up during the program execution, the time complexity for searching a string remains constant.
import random
import math
import urllib, json
from pyvis.network import Network
import matplotlib.pyplot as plt
class TrieNode:
def __init__(self, inputChar):
self.char = inputChar
self.end = False
self.children = {}
class Trie():
def __init__(self, startingElements=None):
self.root = TrieNode("")
if startingElements!=None:
for i in startingElements: self.insert(i)
def insert(self, word):
node = self.root
for char in word:
if char in node.children:
node = node.children[char]
else:
new_node = TrieNode(char)
node.children[char] = new_node
node = new_node
node.end = True
def searchAndSplit(self, x):
node = self.root
output = ["", ""]
for char in x:
if char in node.children:
node = node.children[char]
else:
return []
output[1 if node.end else 0] += node.char
return output if node.end else []
def remove(self, root, word, index = 0):
if not root:
return None
if index==len(word):
if root.end:
root.end = False
if root.children=={}:
del root
root = None
return root
root.children[word[index]] = self.remove(root.children[word[index]], word, index + 1)
if (root.children=={}) and not root.end:
del root
root = None
return rootAbove, you can see the whole implementation. In short, it consists of two classes, TrieNode and Trie, which define the Trie's nodes and Trie structure itself, respectively.
The Trie class provides methods for inserting, searching, splitting (which is a custom feature we will discuss in the visualization section), and removing words from the Trie. The TrieNode class represents individual nodes and their associated attributes. In this case, they are a string containing the corresponding node character and a hash table of characters associated with the pointers to the Trie's subbranches.
How to Visualize a Trie
Finally, after functionally implementing the Trie, we will use the Python library pyvis to define a function inside the Trie class that automatically produces a graph visualization of the data structure. This will result in an HTML file in which we can interact with the elements it contains.
def toGraph(self):
g = Network(directed =True)
g.show_buttons()
nodeIndex = 1
currentNode = 0
q = [self.root]
g.add_node(currentNode, label="", color="red")
tempLabels = {0:""}
while q!=[]:
n = q.pop(0)
for i in n.children.values():
if i:
tempLabels[nodeIndex] = tempLabels[currentNode]+i.char
g.add_node(nodeIndex, label=tempLabels[currentNode]+i.char, color="#48e073" if i.end else "blue")
g.add_edge(currentNode, nodeIndex)
nodeIndex+=1
q.append(i)
currentNode+=1
g.show('nx.html')As you can observe in the toGraph() function, we perform a Breadth-First Search all over the Trie while creating the necessary nodes and edges (connections between them) inside a pyvis.network.Network object.
Also, it gives the end nodes a different color from the rest. This will help us understand the benefits that this visualization provides so we can simplify the execution of functions related to the processing and validation of strings in the previous example.
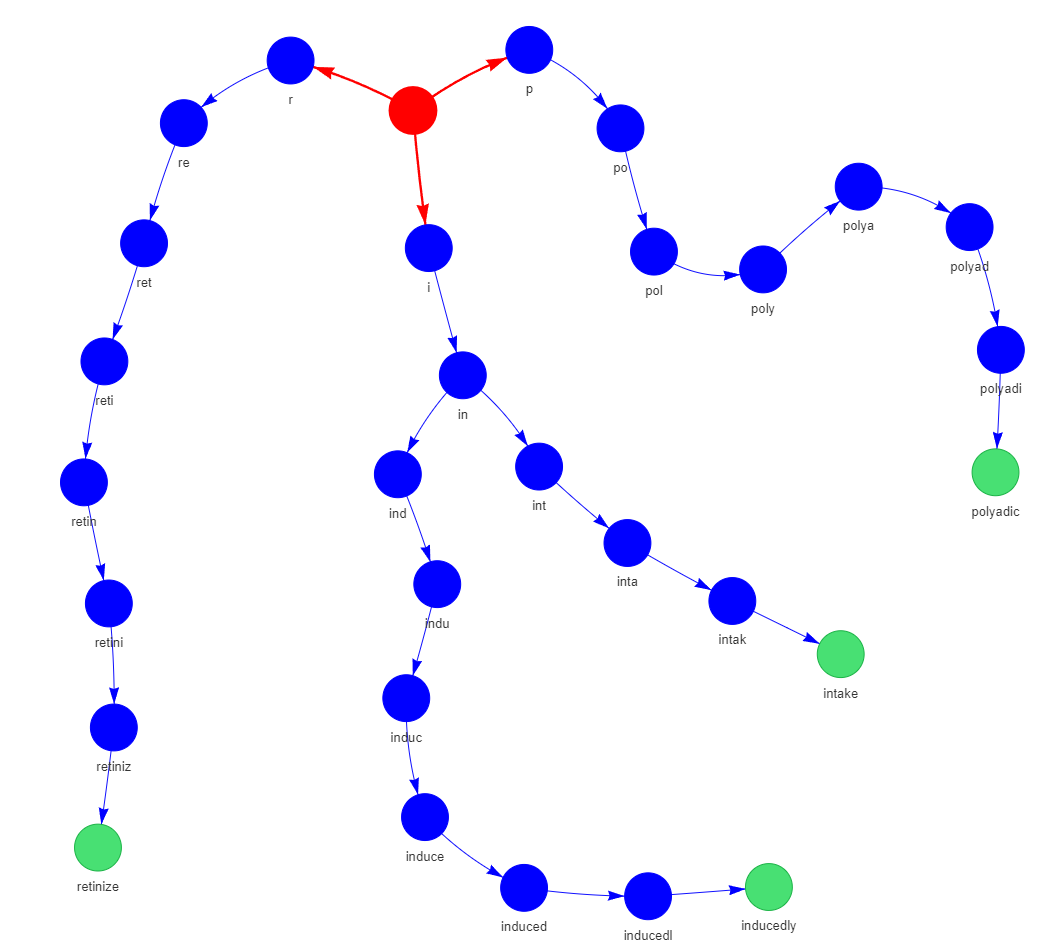
So to instantiate a Trie with the string coordinates of the example 6x6 board, we will pass a generator Python object to the Trie's constructor to insert each string into the data structure and plot it into a graph:
tr = Trie((''.join(chr(97+int(j)) for j in str(i))+str(k) for k in range(6) for i in range(6)))
tr.toGraph()
According to the coloring rules of the toGraph() function, all nodes containing only an alphabetic character are colored in blue, while all other nodes except the root one are colored in green.
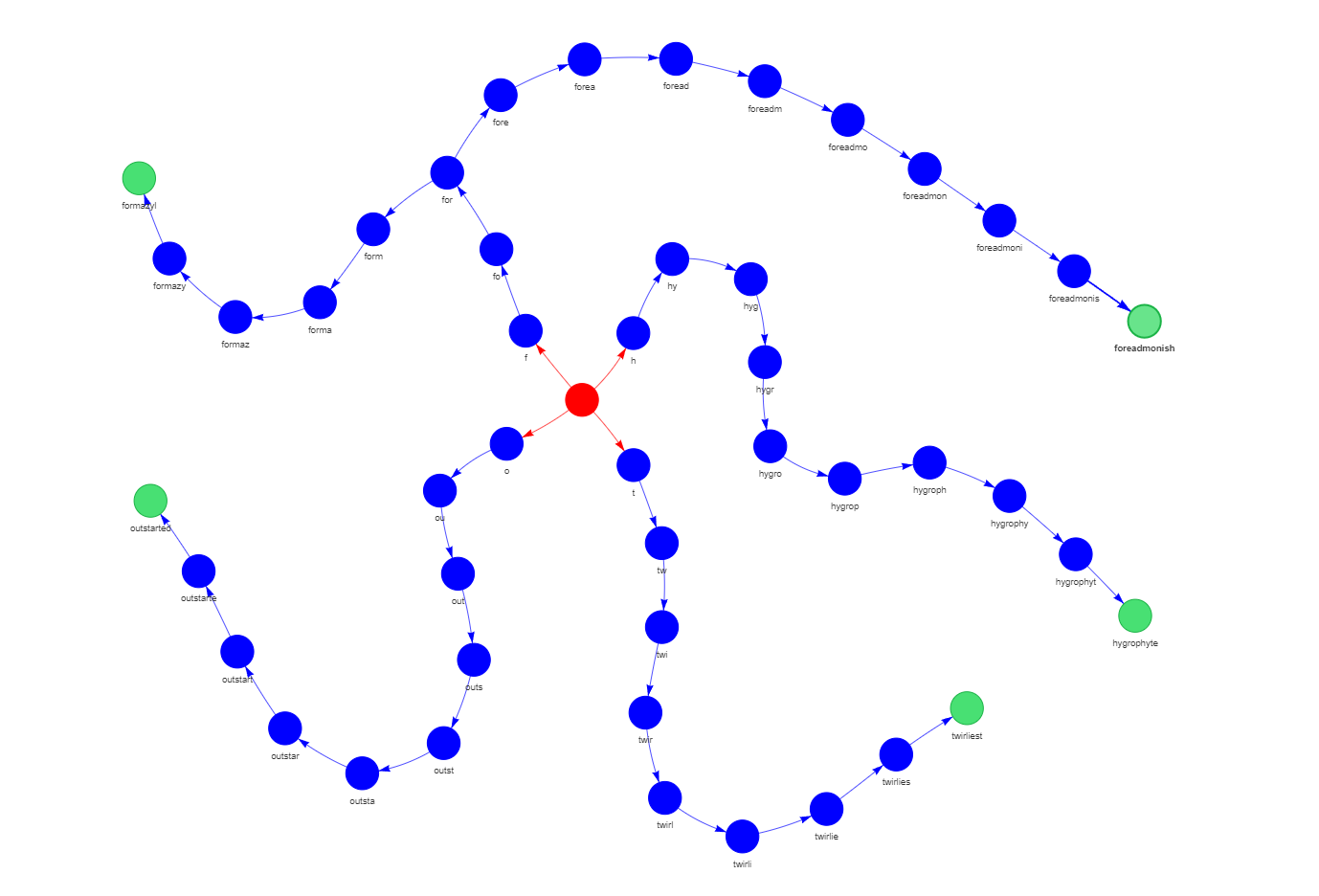
If we increase the board size, we will notice that all the end nodes will have a different color than the nodes with alphabetic characters, as shown in the following graph section of a 16x16 board:
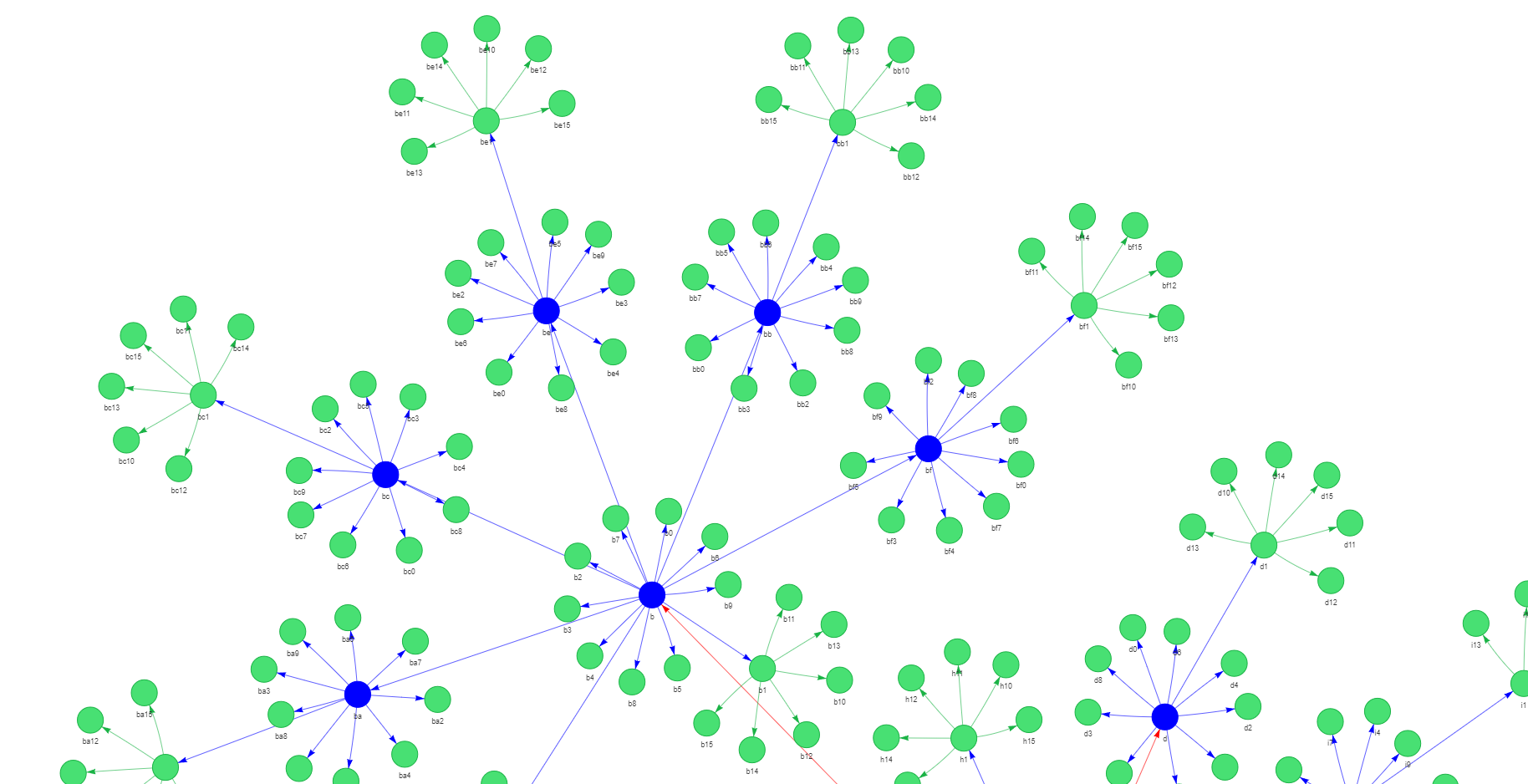
Thus, when performing a search or a BFS traversal, we can take advantage of the end flag to split the coordinates between alphabetic and numeric characters. This avoids an extra post-processing step after validating the user input.
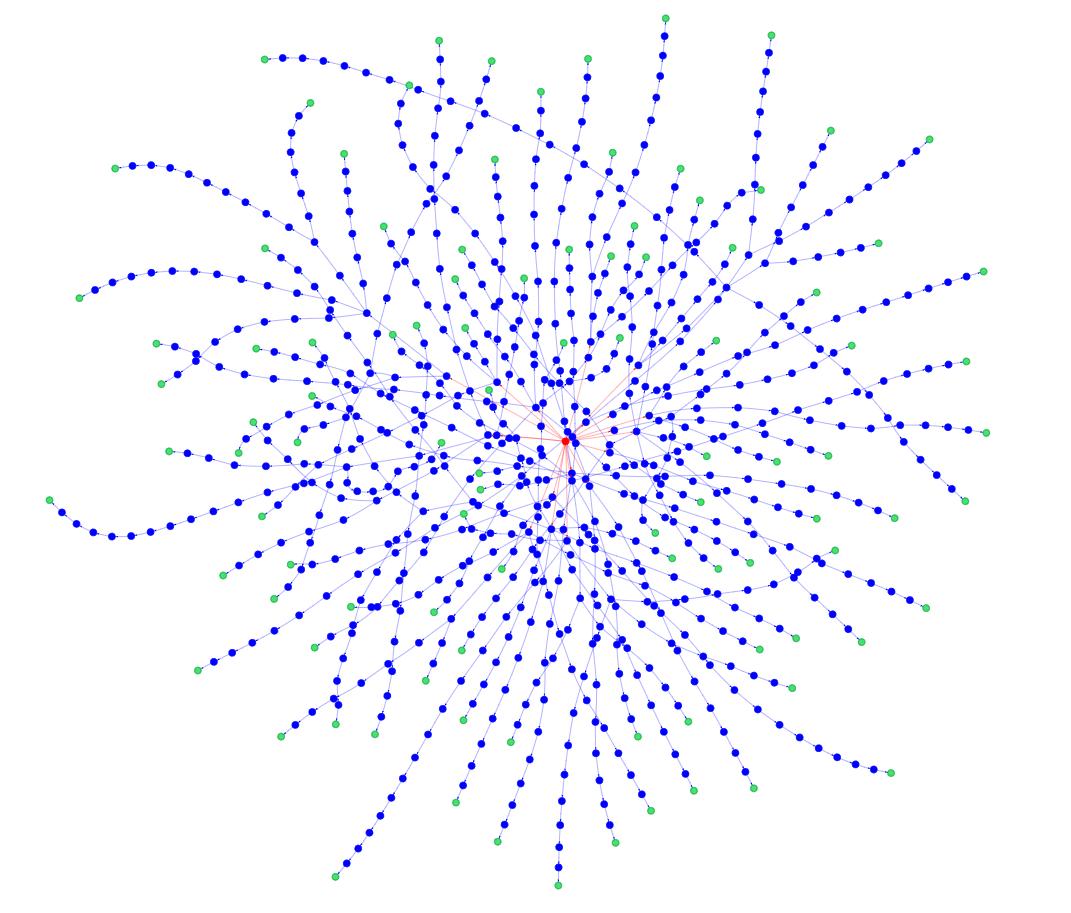
Lastly, we can create a bigger Trie to see how it behaves on a larger scale.
data = json.loads(urllib.request.urlopen("https://raw.githubusercontent.com/dwyl/english-words/master/words_dictionary.json").read())
data = list(data.keys())
tr = Trie(random.sample(data, 100))
tr.toGraph()By using this code, we are accessing an open-source English words dataset, selecting 100 random words, and inserting them into a new Trie. It gives as visualization output the following graph:

If you would like to work and customize Tries for specific projects interactively, you can access the complete code in the Colab Notebook provided below:
Conclusion
We have seen how visualizing a data structure or a problem input data can significantly enhance our understanding of its relationships and intricacies. It also offers us the chance to introduce new features that otherwise could not have been developed so easily without a proper and automated visioning.
In addition to Tries, the benefits of visualization can be extended to other data structures and algorithms. And it can foster a deeper understanding of the underlying logic and functionality.
Incorporating visualization techniques into the development process can significantly improve the efficiency and creativity of our work in computer science and data analysis.
In conclusion, by embracing visualization as a key component of our development process, we can unlock new opportunities for optimizing, troubleshooting and exploring the full potential of data structures and algorithms in various applications.