A guided tour on implementing visualization modules with dynamic datasets
It is common to remove the existing Scalable Vector Graphics (SVG) element by calling d3.select('#chart').remove(), before rendering a new chart.
However, there may be scenarios when you have to produce dynamic visualizations from sources such as external APIs. This article will show you how to do this using D3.js.
D3.js handles dynamic data by adopting the general update pattern. This is commonly described as a data-join, followed by operations on the enter, update and exit selections. Mastering these selection methods will enable you to produce seamless transitions between states, allowing you to tell meaningful stories with data.
Getting Started
Requirements
We will be building a graph that illustrates the movement of a few Exchange-Traded Funds (ETFs) over the second half of 2018. The graph consists of the following tools:
- Closing price line chart
- Trade volume bar chart
- 50-day simple moving average
- Bollinger Bands (20-day simple moving average, with standard deviation set at 2.0)
- Open-high-low-close (OHLC) chart
- Candlesticks
These tools are commonly utilized in the technical analysis of stocks, commodities, and other securities. For example, traders may make use of the Bollinger Bands and Candlesticks to derive patterns which represent buy or sell signals.
This is how the graph will look like:
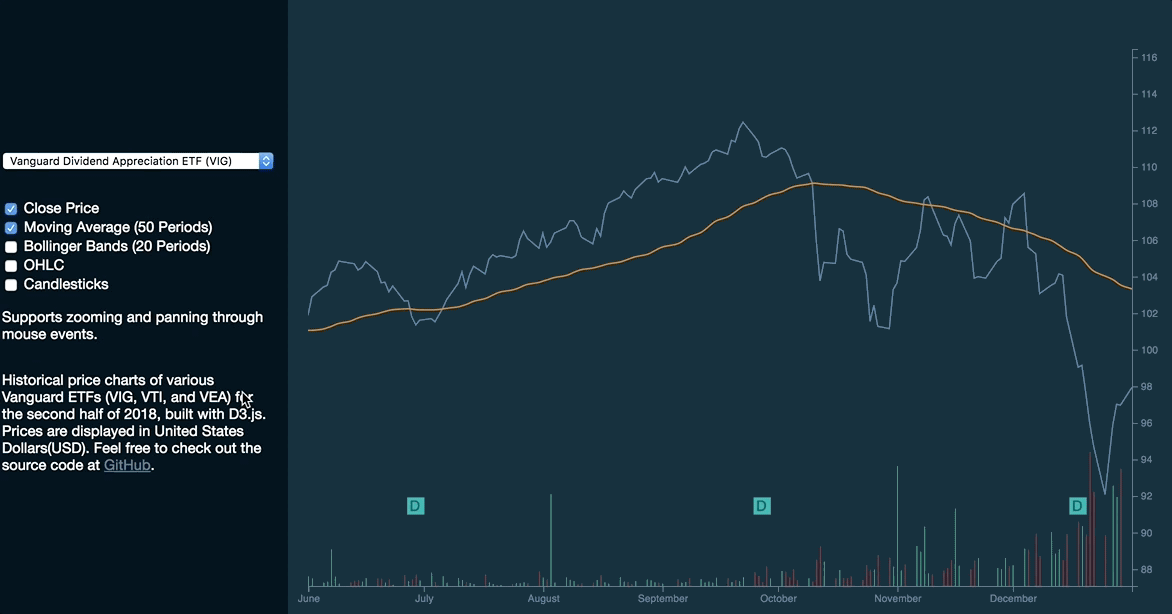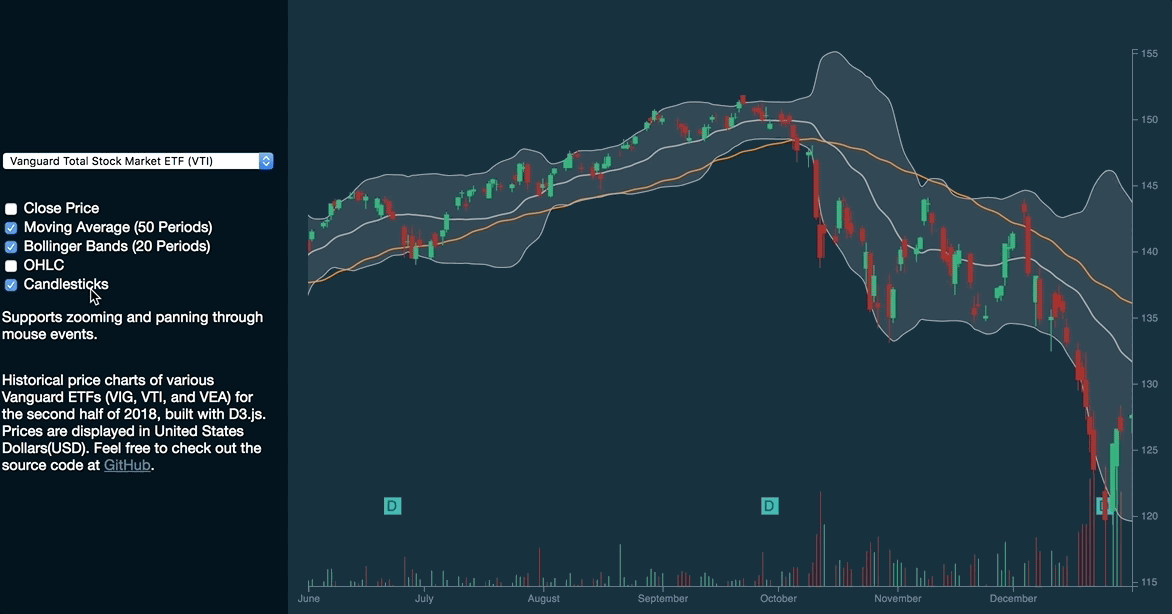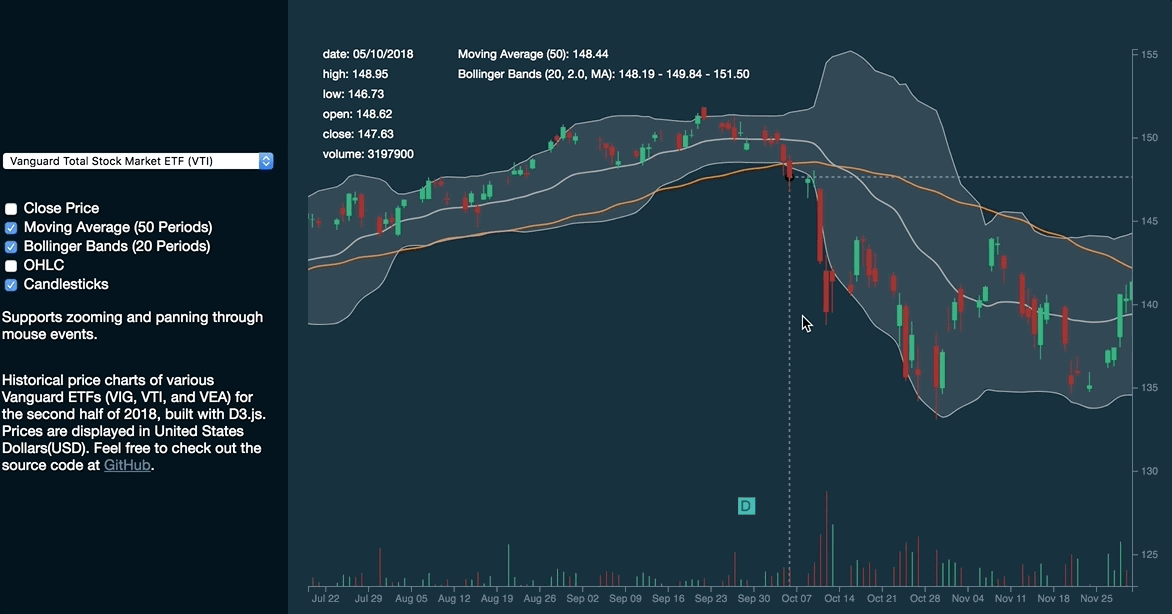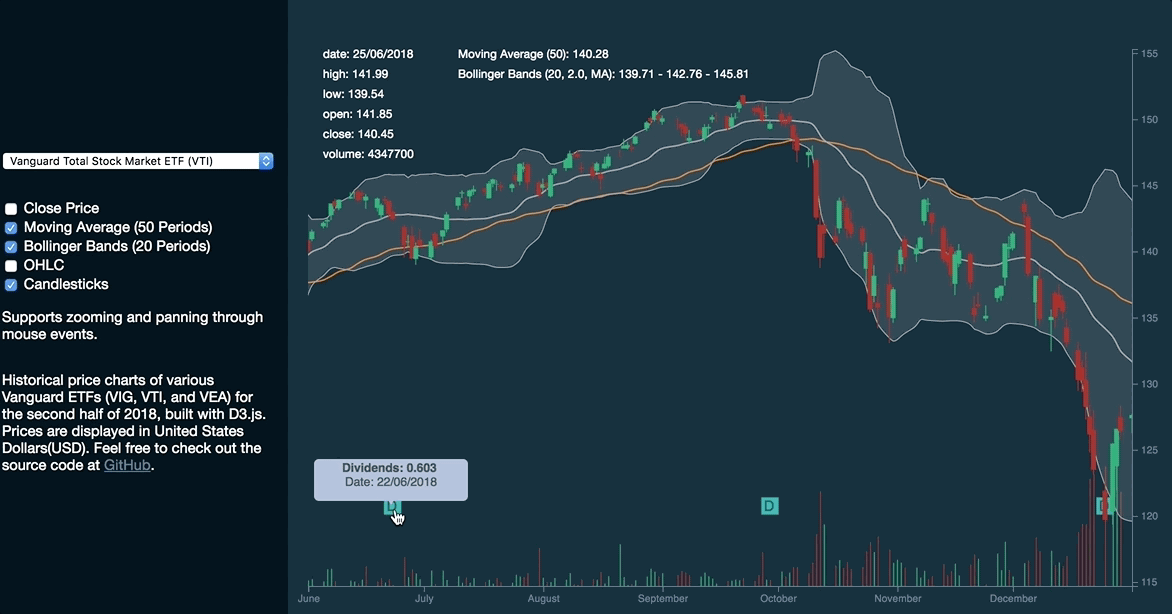
This article aims to equip you with the fundamental theories of data joins and the enter-update-exit pattern in order to allow you to easily visualize dynamic datasets. In addition, we will be covering selection.join, which is introduced in D3.js’s v5.8.0 release.
The general update pattern
The gist of the general update pattern is the selection of Document Object Model (DOM) elements, followed by binding of data to these elements. These elements are then created, updated or removed, to represent the necessary data.
Joining new data
Data join is the mapping of n number of elements in the dataset with nnumber of selected Document Object Model (DOM) nodes, specifying the required action to the DOM as the data changes.
We use the data() method to map each data point to a corresponding element in the DOM selection. In addition, it is good practice to maintain object constancy by specifying a key as the unique identifier in each data point. Let’s take a look at the following example, which is the first step towards rendering the trade volume bars:
const bars = d3
.select('#volume-series')
.selectAll(.'vol')
.data(this.currentData, d => d['date']);The above line of code selects all elements with the class vol , followed by mapping the this.currentData array with the selection of DOM elements using the data() method.
The second optional argument of data() takes a data point as input and returns the date property as the selected key for each data point.
Enter/Update selection
.enter() returns an enter selection which represents the elements that need to be added when the joined array is longer than the selection. This is followed by calling .append(), which creates or updates elements on the DOM. We can implement this in the following manner:
bars
.enter()
.append('rect')
.attr('class', 'vol')
.merge(bars)
.transition()
.duration(750)
.attr('x', d => this.xScale(d['date']))
.attr('y', d => yVolumeScale(d['volume']))
.attr('fill', (d, i) => {
if (i === 0) {
return '#03a678';
} else {
// green bar if price is rising during that period, and red when price is falling
return this.currentData[i - 1].close > d.close
? '#c0392b'
: '#03a678';
}
})
.attr('width', 1)
.attr('height', d => this.height - yVolumeScale(d['volume']));.merge() merges the update and enter selections, before applying the subsequent method chains to create animations between transitions, and to update their associated attributes. The above block of code enables you to perform the following actions on the selected DOM elements:
- The update selection, which consists of data points represented by the
<rect>elements on the graph, will have their attributes updated accordingly. - The creation of
<rect>elements with the classvol, with the above attributes defined within each element as the enter selection consists of data points that are not represented on the graph.
Exit selection
Remove items from our dataset by following the simple steps below:bars.exit().remove();
.exit() returns an exit selection, which specifies the data points that need to be removed. The .remove() method subsequently deletes the selection from the DOM.
This is how the volume series bars will respond to changes in data:
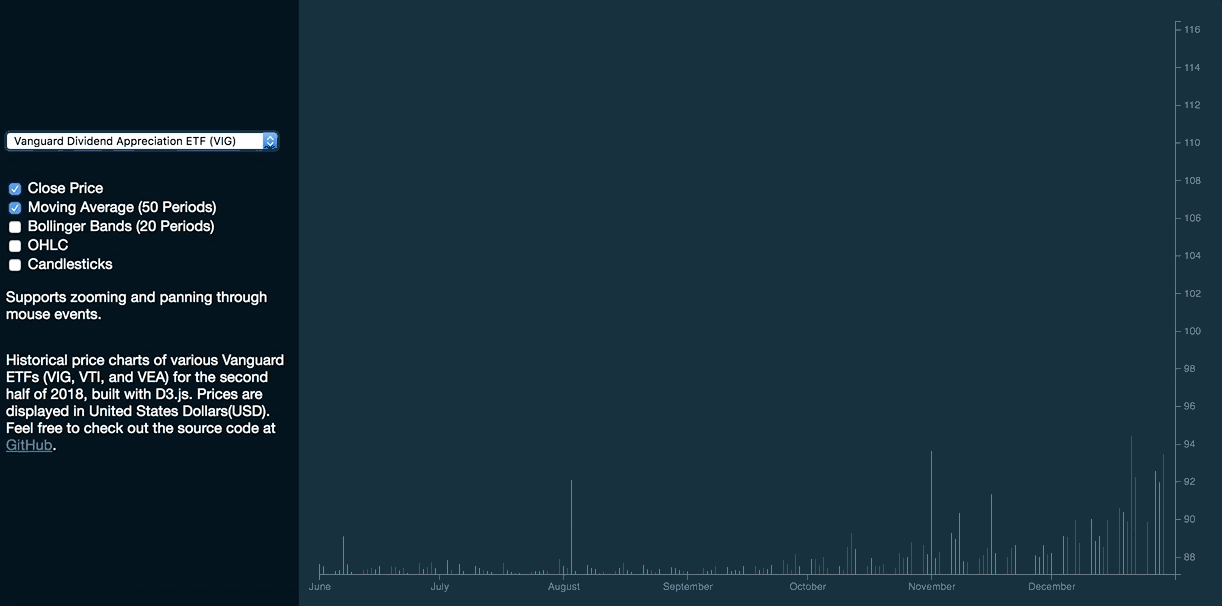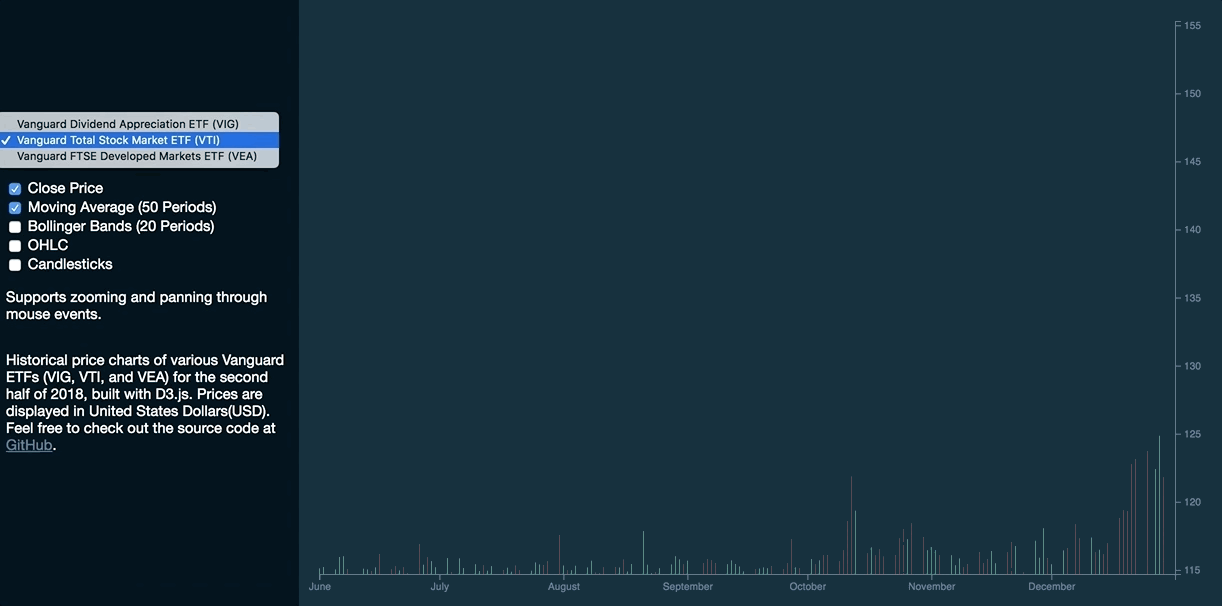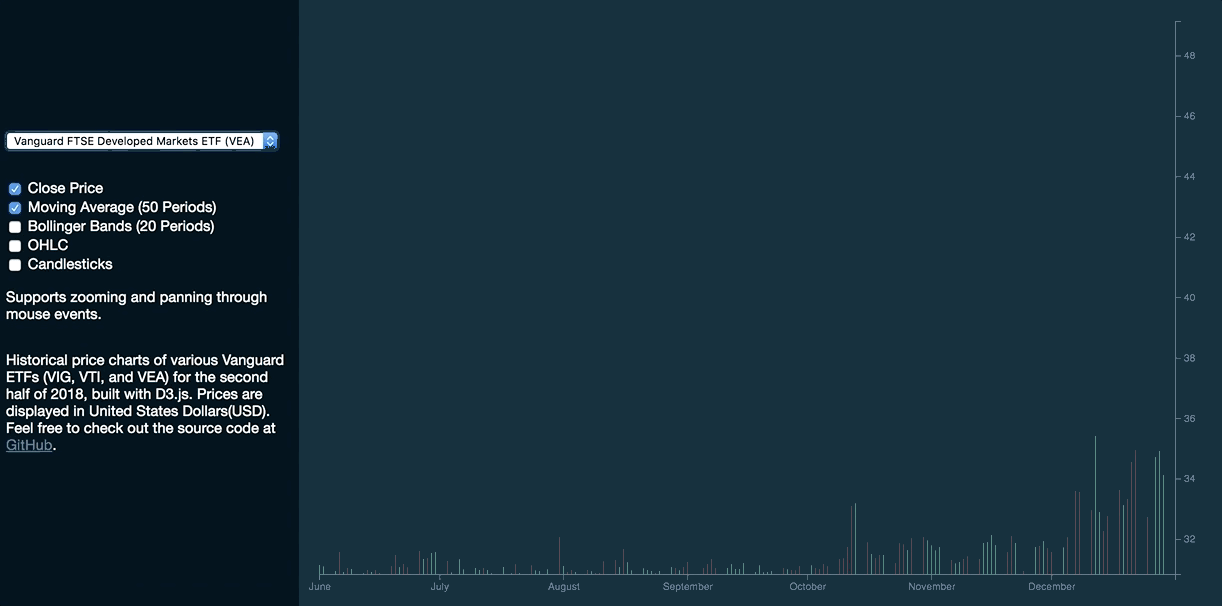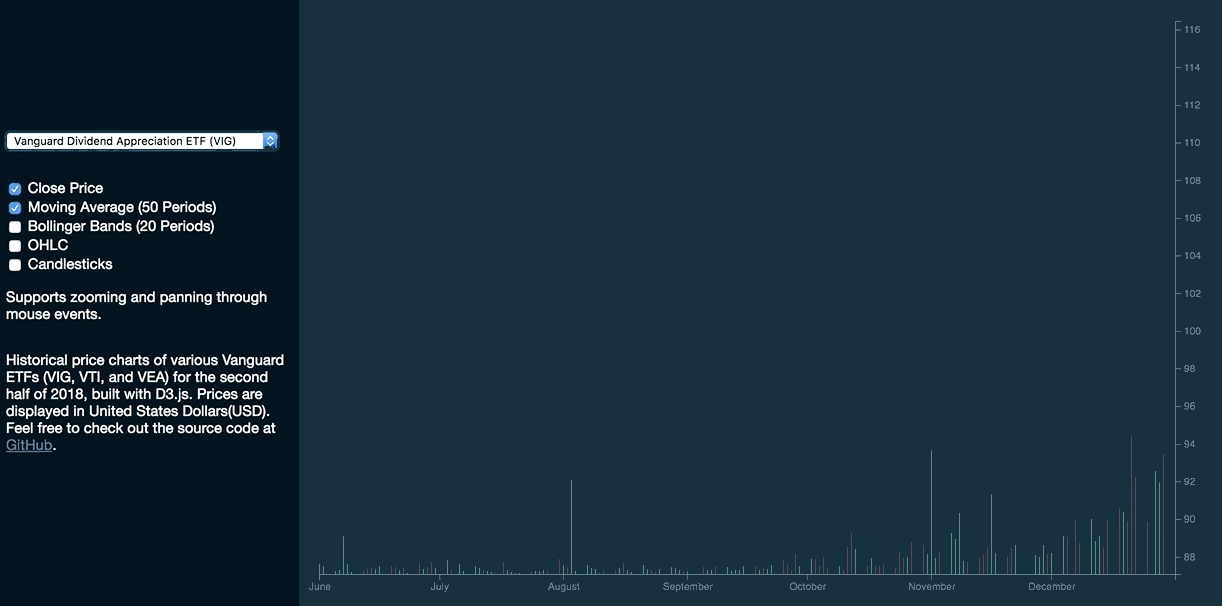
Take note of how the DOM and the respective attributes of each <rect>element are updated as we select a different dataset:
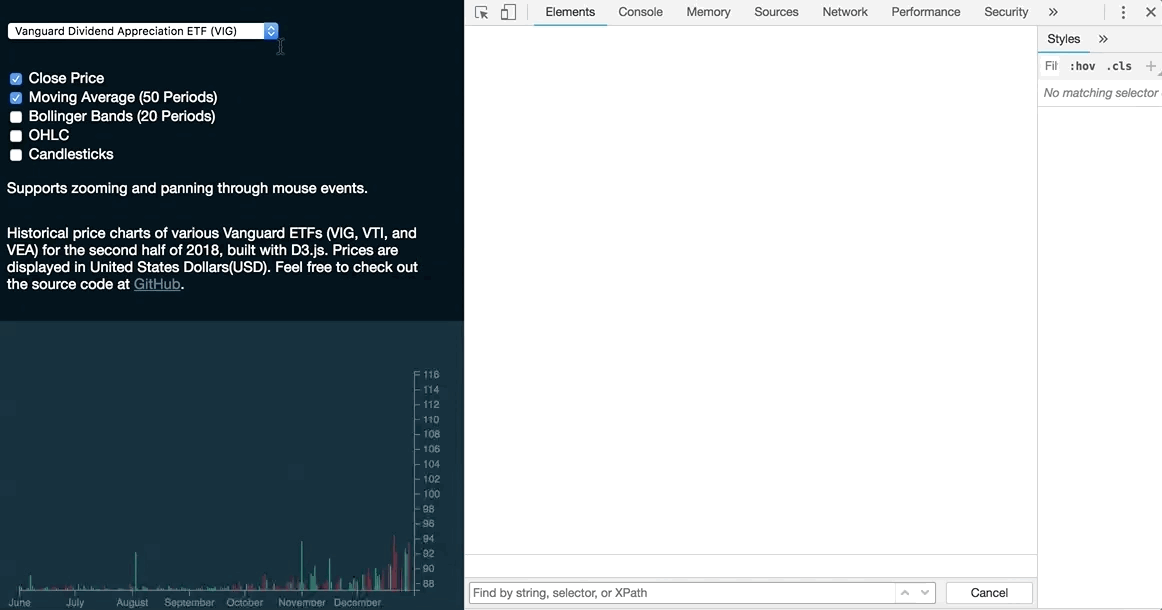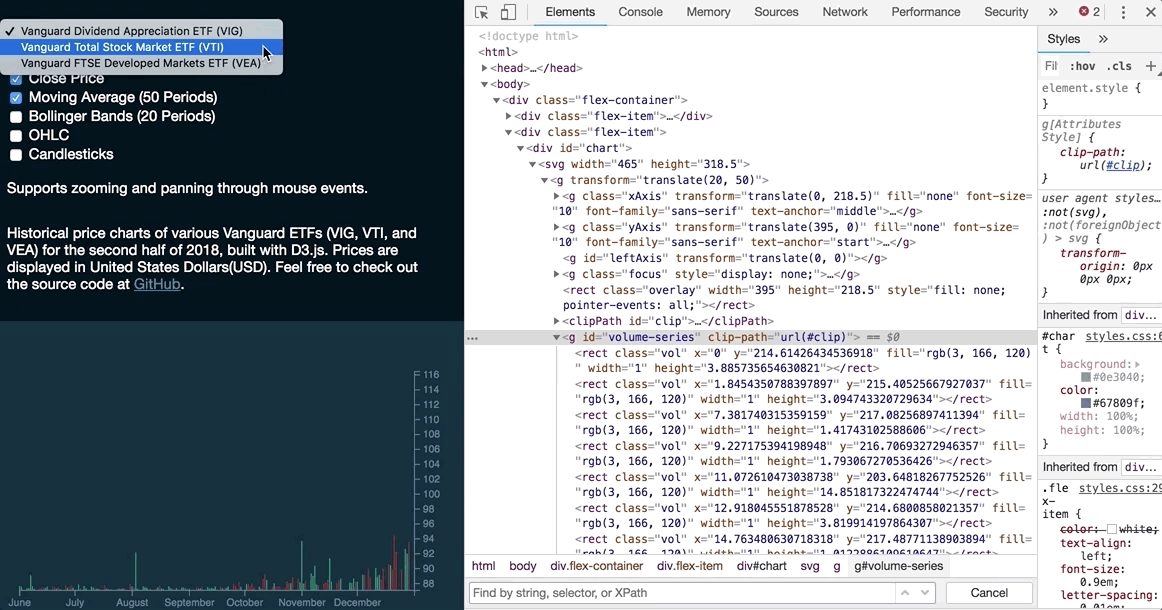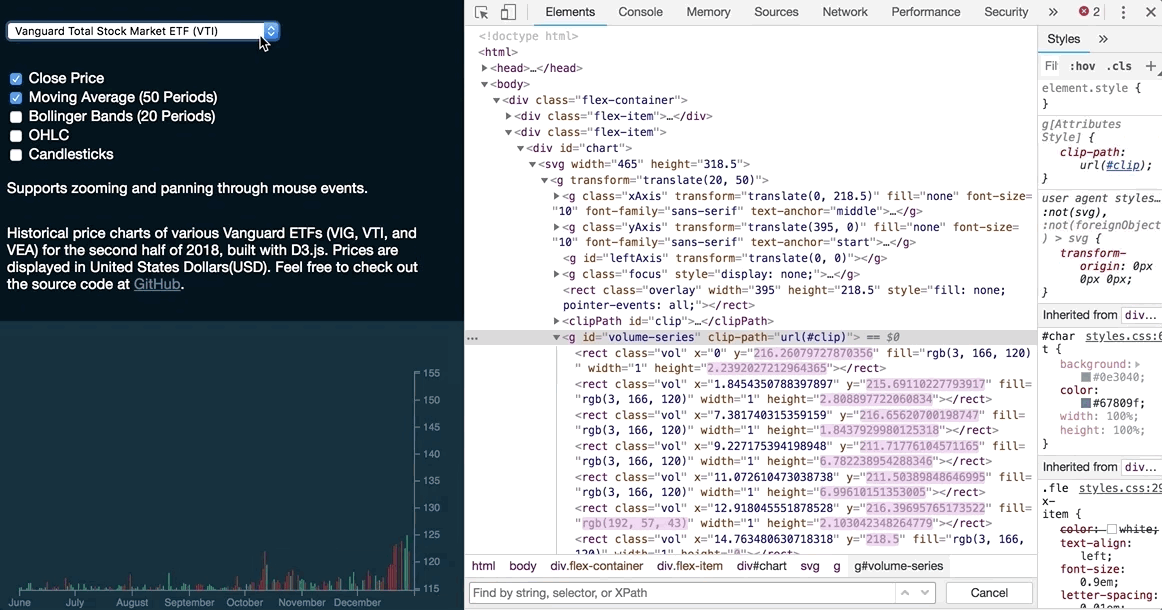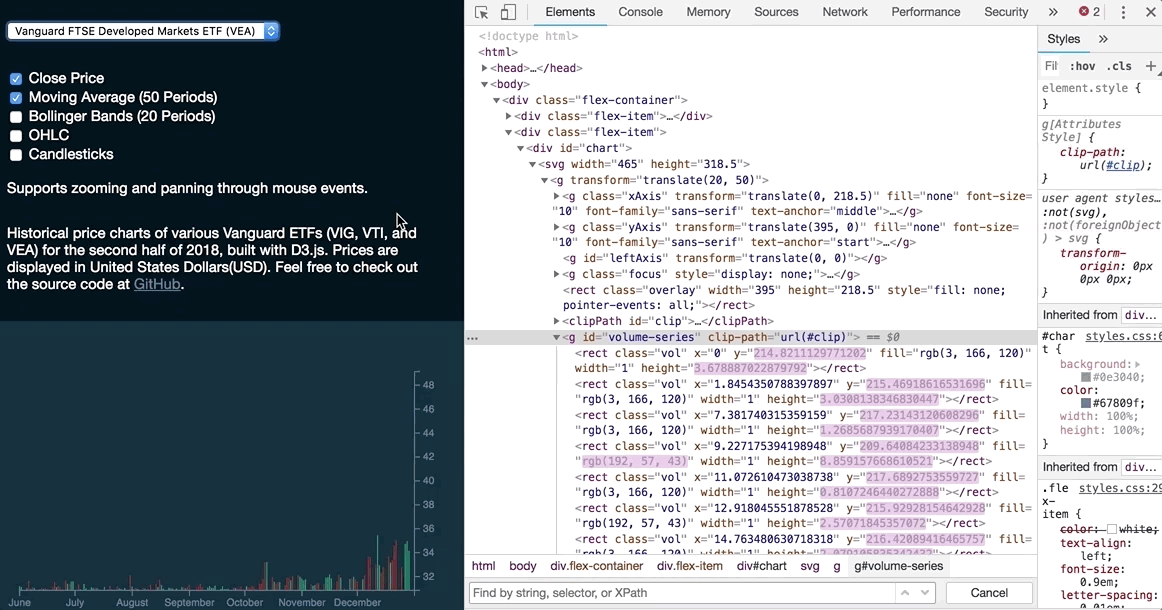
Selection.join (as of v5.8.0)
The introduction of selection.join in v5.8.0 of D3.js has simplified the entire data join process. Separate functions are now passed to handle enter, update, and exit which in turn returns the merged enter and update selections.
selection.join(
enter => // enter.. ,
update => // update.. ,
exit => // exit..
)
// allows chained operations on the returned selectionsIn the case of the volume series bars, the application of selection.join will result in the following changes on our code:
//select, followed by updating data join
const bars = d3
.select('#volume-series')
.selectAll('.vol')
.data(this.currentData, d => d['date']);
bars.join(
enter =>
enter
.append('rect')
.attr('class', 'vol')
.attr('x', d => this.xScale(d['date']))
.attr('y', d => yVolumeScale(d['volume']))
.attr('fill', (d, i) => {
if (i === 0) {
return '#03a678';
} else {
return this.currentData[i - 1].close > d.close
? '#c0392b'
: '#03a678';
}
})
.attr('width', 1)
.attr('height', d => this.height - yVolumeScale(d['volume'])),
update =>
update
.transition()
.duration(750)
.attr('x', d => this.xScale(d['date']))
.attr('y', d => yVolumeScale(d['volume']))
.attr('fill', (d, i) => {
if (i === 0) {
return '#03a678';
} else {
return this.currentData[i - 1].close > d.close
? '#c0392b'
: '#03a678';
}
})
.attr('width', 1)
.attr('height', d => this.height - yVolumeScale(d['volume']))
);Also, note that we have made some changes to the animation of the bars. Instead of passing the transition() method to the merged enter and update selections, it is now used in the update selection such that transitions will only be applied when the dataset has changed.
The returned enter and update selections are then merged and returned by selection.join.
Bollinger Bands
Similarly, we can apply selection.join on the rendering of Bollinger Bands. Before rendering the Bands, we are required to calculate the following properties of each data point:
- 20-day simple moving average.
- The upper and lower bands, which have a standard deviation of 2.0 above and below the 20-day simple moving average, respectively.
This is the formula for calculating standard deviation:
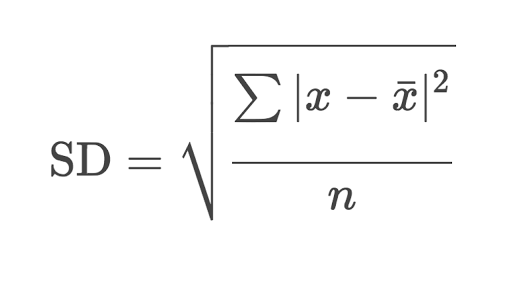
Now, we shall translate the above formula into JavaScript code:
calculateBollingerBands(data, numberOfPricePoints) {
let sumSquaredDifference = 0;
return data.map((row, index, total) => {
const start = Math.max(0, index - numberOfPricePoints);
const end = index;
// divide the sum with subset.length to obtain moving average
const subset = total.slice(start, end + 1);
const sum = subset.reduce((a, b) => {
return a + b['close'];
}, 0);
const sumSquaredDifference = subset.reduce((a, b) => {
const average = sum / subset.length;
const dfferenceFromMean = b['close'] - average;
const squaredDifferenceFromMean = Math.pow(dfferenceFromMean, 2);
return a + squaredDifferenceFromMean;
}, 0);
const variance = sumSquaredDifference / subset.length;
return {
date: row['date'],
average: sum / subset.length,
standardDeviation: Math.sqrt(variance),
upperBand: sum / subset.length + Math.sqrt(variance) * 2,
lowerBand: sum / subset.length - Math.sqrt(variance) * 2
};
});
}
.
.
// calculates simple moving average, and standard deviation over 20 days
this.bollingerBandsData = this.calculateBollingerBands(validData, 19);A quick explanation of the calculation of the standard deviation, and Bollinger Band values on the above block of code is as follows:
For each iteration,
- Calculate the average of the close price.
- Find the difference between the average value and close price for that data point.
- Square the result of each difference.
- Find the sum of squared differences.
- Calculate the mean of the squared differences to get the variance
- Get the square root of the variance to obtain the standard deviation for each data point.
- Multiply the standard deviation by 2. Calculate the upper and lower band values by adding or subtracting the average with the multiplied value.
With the data points defined, we can then make use of selection.join to render Bollinger Bands:
// code not shown: rendering of upper and lower bands
.
.
// bollinger bands area chart
const area = d3
.area()
.x(d => this.xScale(d['date']))
.y0(d => this.yScale(d['upperBand']))
.y1(d => this.yScale(d['lowerBand']));
const areaSelect = d3
.select('#chart')
.select('svg')
.select('g')
.selectAll('.band-area')
.data([this.bollingerBandsData]);
areaSelect.join(
enter =>
enter
.append('path')
.style('fill', 'darkgrey')
.style('opacity', 0.2)
.style('pointer-events', 'none')
.attr('class', 'band-area')
.attr('clip-path', 'url(#clip)')
.attr('d', area),
update =>
update
.transition()
.duration(750)
.attr('d', area)
);This renders the area chart which denotes the area filled by the Bollinger Bands. On the update function, we can use the selection.transition()method to provide animated transitions on the update selection.
Candlesticks
The candlesticks chart displays the high, low, open and close prices of a stock for a specific period. Each candlestick represents a data point. Green represents when the stock closes higher while red represents when the stock closes at a lower value.

Unlike the Bollinger Bands, there is no need for additional calculations, as the prices are available in the existing dataset.
const bodyWidth = 5;
const candlesticksLine = d3
.line()
.x(d => d['x'])
.y(d => d['y']);
const candlesticksSelection = d3
.select('#chart')
.select('g')
.selectAll('.candlesticks')
.data(this.currentData, d => d['volume']);
candlesticksSelection.join(enter => {
const candlesticksEnter = enter
.append('g')
.attr('class', 'candlesticks')
.append('g')
.attr('class', 'bars')
.classed('up-day', d => d['close'] > d['open'])
.classed('down-day', d => d['close'] <= d['open']);
On the enter function, each candlestick is rendered based on its individual properties.
First and foremost, each candlestick group element is assigned a class of up-day if the close price is higher than the open price, and down-day if the close price is lower than or equal to the open-price.
candlesticksEnter
.append('path')
.classed('high-low', true)
.attr('d', d => {
return candlesticksLine([
{ x: this.xScale(d['date']), y: this.yScale(d['high']) },
{ x: this.xScale(d['date']), y: this.yScale(d['low']) }
]);
});Next, we append the path element, which represents the highest and lowest price of that day, to the above selection.
candlesticksEnter
.append('rect')
.attr('x', d => this.xScale(d.date) - bodyWidth / 2)
.attr('y', d => {
return d['close'] > d['open']
? this.yScale(d.close)
: this.yScale(d.open);
})
.attr('width', bodyWidth)
.attr('height', d => {
return d['close'] > d['open']
? this.yScale(d.open) - this.yScale(d.close)
: this.yScale(d.close) - this.yScale(d.open);
});
});This is followed by appending the rect element to the selection. The height of each rect element is directly proportionate to its day range, derived by subtracting the open price with the close price.
On our stylesheets, we will define the following CSS properties to our classes making the candlesticks red or green:
.bars.up-day path {
stroke: #03a678;
}
.bars.down-day path {
stroke: #c0392b;
}
.bars.up-day rect {
fill: #03a678;
}
.bars.down-day rect {
fill: #c0392b;
}This results in the rendering of the Bollinger Bands and candlesticks:
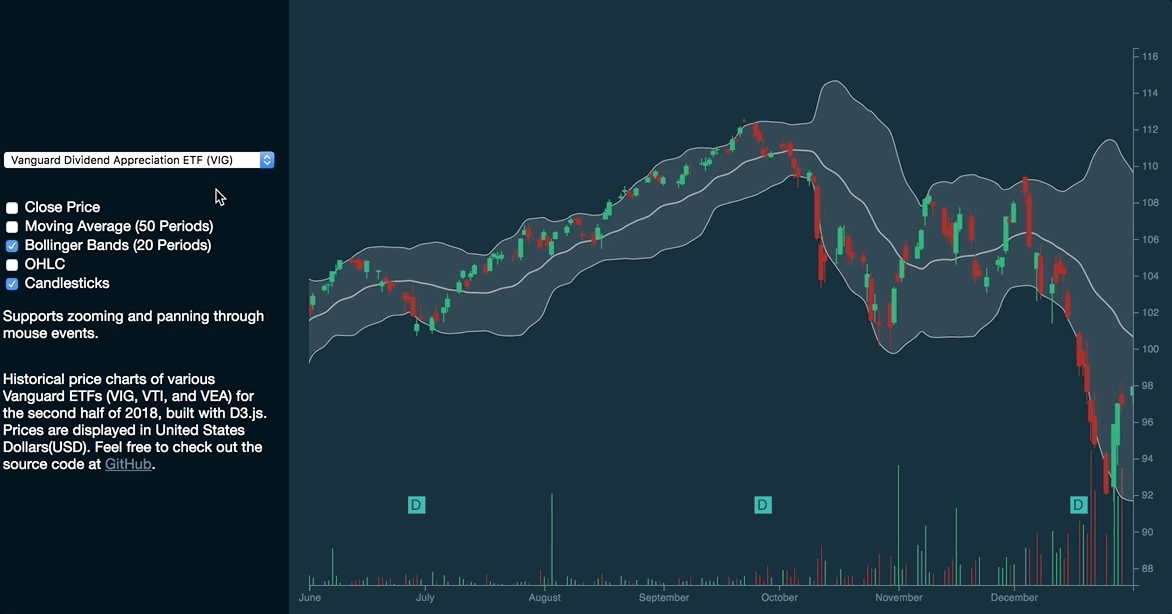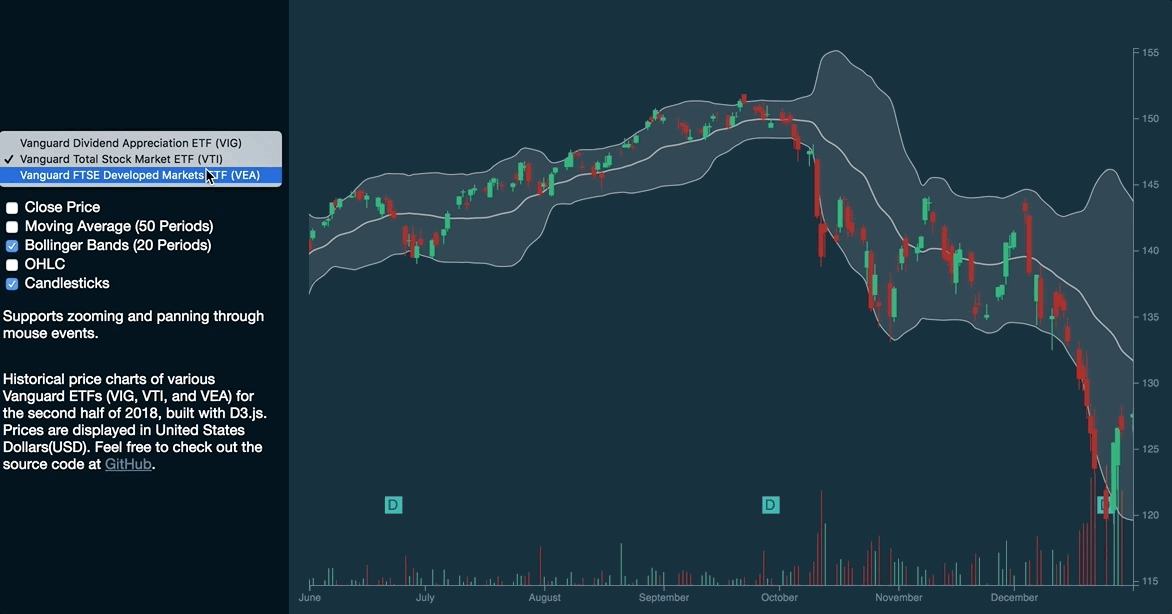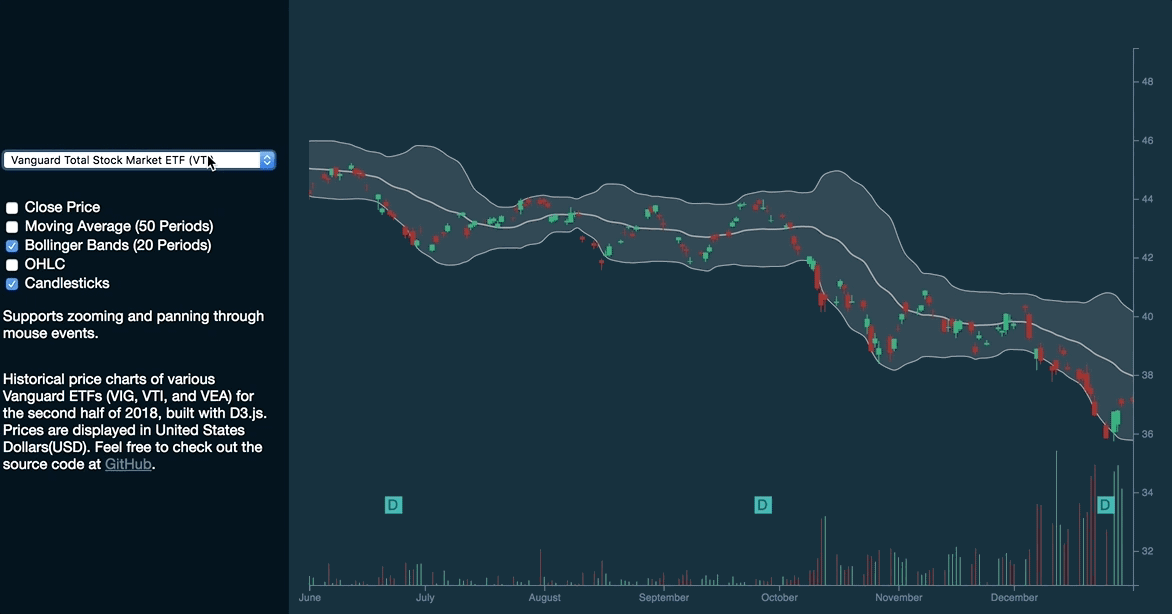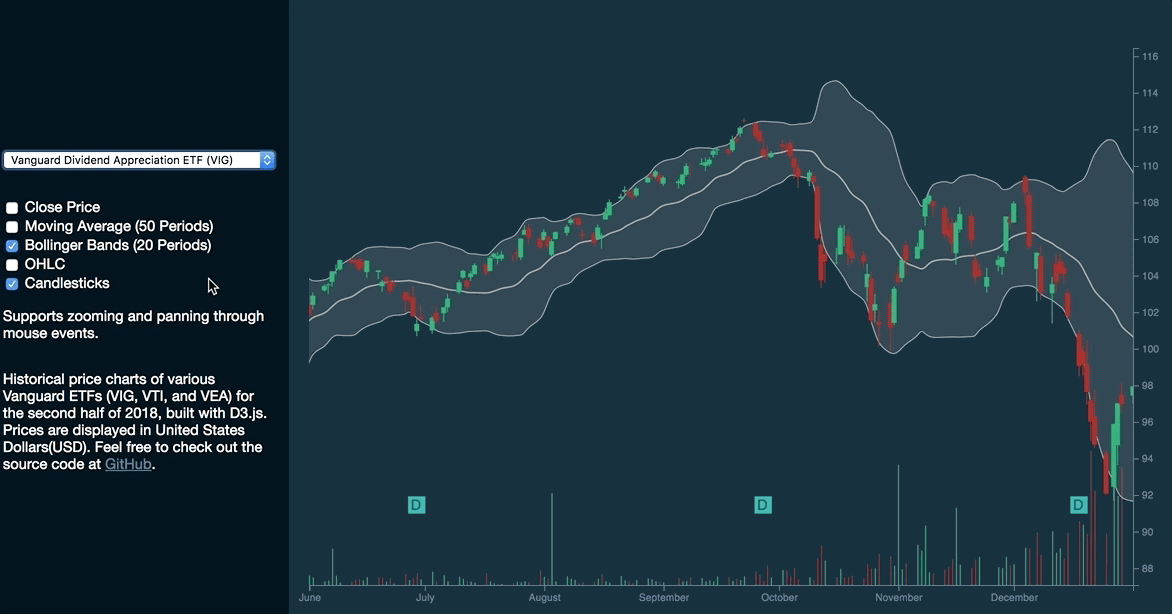
The new syntax has proven to be simpler and more intuitive than explicitly calling selection.enter, selection.append, selection.merge, and selection.remove.
Note that for those who are developing with D3.js’s v5.8.0 and beyond, it has been recommended by Mike Bostock that these users start using selection.join due to the above advantages.
Conclusion
The potential of D3.js is limitless and the above illustrations are merely the tip of the iceberg. Many satisfied users have created visualizations which are vastly more complex and sophisticated than the one show above. This list of free APIs may interest you if you are keen to embark on your own data visualization projects.
Feel free to check out the source code and the full demonstration of this project.
Thank you very much for reading this article. If you have any questions or suggestions, feel free to leave them on the comments below!
New to D3.js? You may refer to this article on the basics of implementing common chart components.
Special thanks to Debbie Leong for reviewing this article.
Additional references: