The Fibonacci Series is a special kind of sequence that starts with 0 and 1, and every number after those two is the sum of the two preceding numbers.
The Fibonacci series goes like this: 0, 1, 1, 2, 3, 5, 8, 13, 21, … and so on. It was first described in Indian mathematics.

The Fibonacci series is used in many fields like finance and tech. You can also see it in many natural processes.
The importance of the Fibonacci series in nature is beautifully explained in Guy Murchie’s Quote
“The Fibonacci Sequence turns out to be the key to understanding how nature designs... and is... a part of the same ubiquitous music of the spheres that build harmony into atoms, molecules, crystals, shells, suns, and galaxies and makes the Universe sing.” ― Guy Murchie, The Seven Mysteries of Life: An Exploration of Science and Philosophy
Do you Know These Facts?
- The ratio of any two consecutive numbers in the Fibonacci series is approximately 1.6. For Example: 21 / 13 = 1.61 and 55 / 34 = 1.61
- November 23 is Fibonacci Day, as the date on this day resembles the Fibonacci series in mm / dd format as it is (11/23).
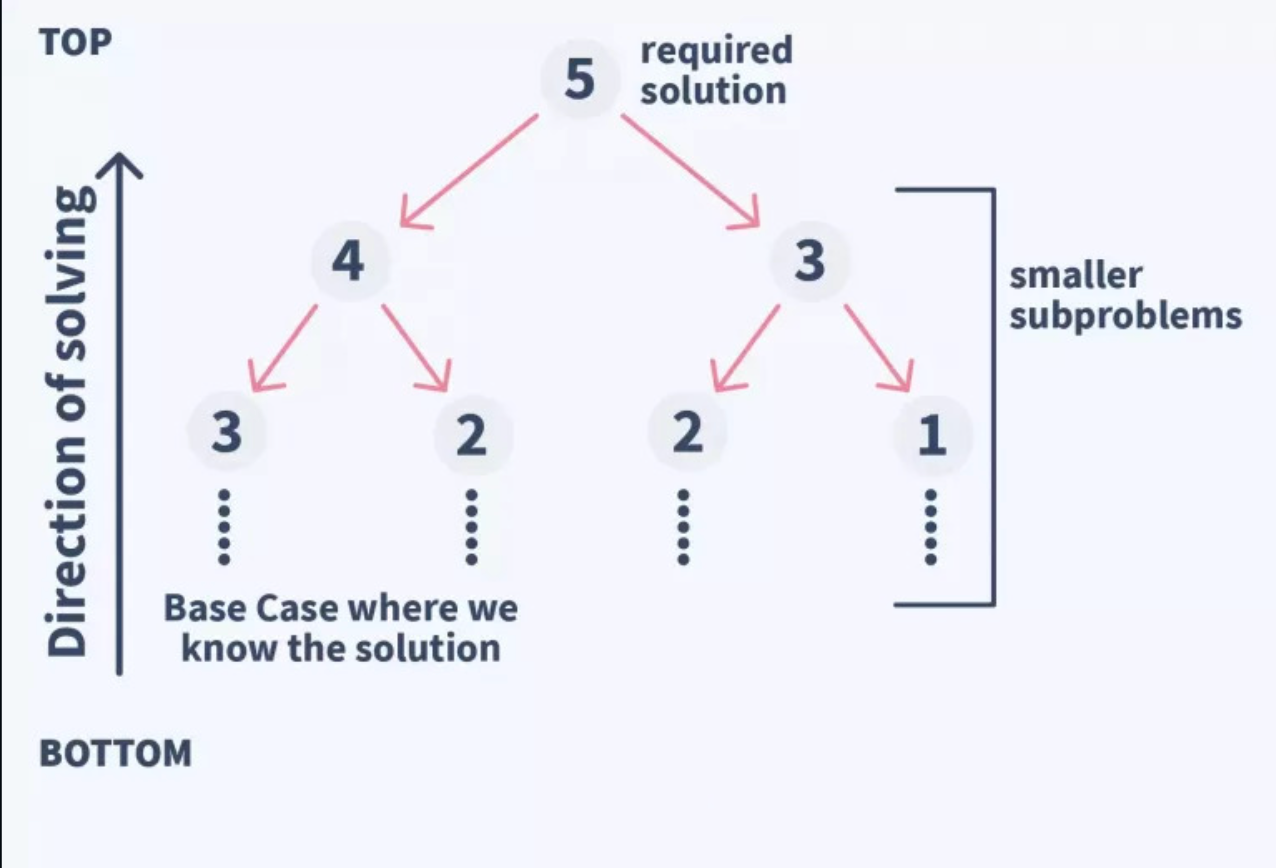
How to Compute the Fibonacci Series using the Top-Down Approach
In this Top-Down approach, we compute the value of the required index as the sum of values at the previous two indexes.
If the previous two values are not available to us, we repeat the same process for them also.
If their values are also not available to us, we repeat the same process until we don’t get the two values. This is an approach that is Theory Driven.
We use the tree kind of approach here – we just look for the previous two values and if those values are not available to us we repeat the process till the time we don’t get the two values.
We break the complex algorithm into smaller fragments that can be called modules. And we can break these modules down further into smaller fragments until they can not be fragmented anymore.
Algorithm for the Top-Down Approach
First, you take the input ‘n’ to get the corresponding number in the Fibonacci Series.
Then, you calculate the value of the required index as a sum of the values at the previous two indexes ( that is add values at the n-1 index and n-2 index). If values are not found for the previous two indexes, you will do the same to find values at that index.
Whenever you get the values for the two consecutive previous indexes, you add them and return the result as the value for the next index.
Then you add the value at the “n - 1” index and ”n - 2 ” index and return the required value.
Advantages of the Top-Down Approach
- Debugging your project becomes more efficient.
- Implementing the code becomes easier.
- It makes the code easy to solve and manage.
- The testing process becomes easier because of separate modules.
Disadvantages of the Top-Down Approach
- There's high dependence on the other modules. Changes in one can affect all other modules.
- It is a slower approach as compared to the Bottom-Up approach in Dynamic programming because of recursion.
How to Compute the Fibonacci Series Using the Bottom-Up Approach
In this Bottom-Up approach, we create an array and fill the values of the first two indexes as 0 and 1, respectively.
After that, we calculate the value of all indexes using these two values to store them in an array.
We can fetch the value from any index to get the corresponding number in the Fibonacci Series.
For Example: if fibNum is an array storing the Fibonacci numbers, then we insert:
fibNum[0] = 0 ; fibNum[1] = 1 ;Then inside an iterative loop with a pointer variable i, we write:
fibNum[i] = fibNum[ i - 1 ] + fibNum[ i - 2 ] ;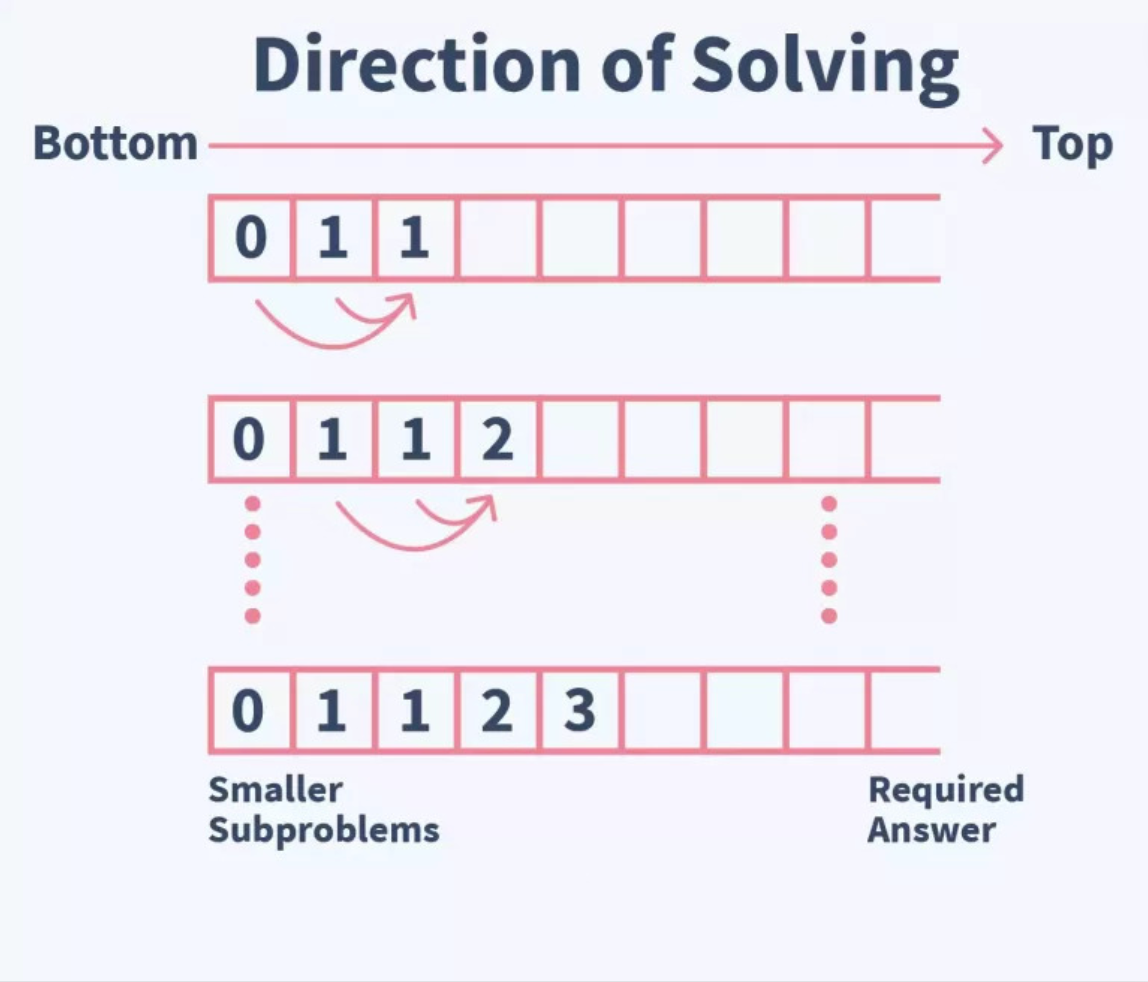
Algorithm for the Bottom-Up Approach
First, you take input ‘n’ to get the corresponding number in the Fibonacci Series.
Then you need to store the values of the Fibonacci series, so you declare an array of size ‘n’ for that.
Next, insert the value for the first two indexes as 0 and 1, respectively.
Use an iterative loop for the third and other remaining indexes as described in the explanation above.
Finally, return the value at the last index of the array.
Advantages of the Bottom-Up Approach
- It is easier to create test cases.
- Your code is reusable
- There's less redundancy because of encapsulation of data and data hiding.
Disadvantages of Bottom-Up Approach
- It sometimes consumes extra space and time.
- Sometimes, it’s hard to understand working in the initial stages.
How to Code the Fibonacci Sequence
There are multiple ways to write a program to find the Fibonacci numbers in Java.
1. How to code the Fibonacci Sequence using simple iterative loops
Here's how to get the nth Fibonacci number Code in Java using a for loop:
import java.util.*;
public class fibonacci{
public static void main(String args[]){
int n,k;
Scanner snr= new Scanner(System.in);
n=snr.nextInt();
snr.close();
int array[]=new int[n];
// The space used here is O(N)
array[0]=0;
array[1]=1;
for(k=2;k<n;k++)array[k]=array[k-1]+array[k-2];
// The array is traversed only once so time complexity is O(N)
System.out.println("Nth number in Fibonacci series is "+array[n-1]);
}
}Here's how to get the nth Fibonacci number code in Java using a while loop:
import java.util.*;
public class fibonacci{
public static void main(String args[]){
int n,k;
Scanner snr= new Scanner(System.in);
n=snr.nextInt();
snr.close();
int array[]=new int[n];
// The space used here is O(N)
array[0]=0;
array[1]=1;
k=2;
while(k<n)
array[k]=array[k-1]+array[k-2];
k++;
System.out.println("Nth number in Fibonacci series is "+array[n-1]);
}
// The array is traversed only once so the time complexity is O(N)
}Time Complexity:
The time complexity for this approach is O(N), which is linear time complexity as we traversed through the array only once.
Space Complexity:
The space complexity for this approach is O(N), which is linear space complexity as we stored answers to sub-problems into an array.
2. How to code the Fibonacci Sequence using recursion
Now we'll go through the algorithm for the Fibonacci Series using recursion in Java.
In recursion, we use a defined function (let's say it's fib here in this code ) to find the Fibonacci number.
In the main() function, we call the function fib() for nth number in the Fibonacci Series.
We define the base case for this recursive call – that is it returns 0 and 1 for the 0th and 1st Fibonacci numbers, respectively.
We will call the function inside itself like fib( x ) = fib( x-1 ) + fib( x-2) until it hits the base case and then we'll obtain the values from there.
How to get the nth Fibonacci number code in Java using recursion
import java.util.*;
public class fibonacci{
public static void main(String args[]){
int n;
Scanner snr= new Scanner(System.in);
n=snr.nextInt();
snr.close();
System.out.println(fib(n));
//Printing number in Fibonacci series
}
public static int fib(int n){
if(n==0){
return 0;
}
// Base cases return itself 0 and 1
else if(n==1){
return 1;
}
else{
return fib(n-1)+fib(n-2);
// Recursive calls
}
}
}Time Complexity:
The time complexity for this approach is O( 2 ^ N ) which is exponential time complexity, where n is the index of the nth Fibonacci number.
We need to find the previous two values for getting each value. For that we call the function two times for each value and the tree can have at most n levels.
This makes around 2 ^ n nodes in the tree.
Space Complexity:
The space Complexity for the approach using recursion is O( 2 ^ N ), which is exponential space complexity where n is the index of nth Fibonacci number.
As we need to store the values for each node and we have 2 ^ N nodes, the total space we need for that is 2 ^ N.
3. How to code the Fibonacci Sequence using recursion with memoization
Memoization means that we keep on storing all the solutions to the subproblems so that we can directly retrieve and use the value wherever we need it in the future in the program. This can save time and space for us.
Algorithm for Fibonacci Series using recursion in Java
Here we define a function (we are using fib()) and use it to find our desired Fibonacci number.
We declare a global array long enough to store all the Fibonacci numbers once calculated.
In the main() function we call the function fib() for the nth number. Then we set the base cases for the recursive call and return 0 and 1, respectively, for the 0th and 1st index.
We call fib(x) = fib( x-1 ) + fib( x-2 ) for all x > 2. For every value computed we store it in the global array.
The value of each Fibonacci number is stored in the corresponding index of the global index. Then we can retrieve and use them for later purposes. This drastically improves the time complexity.
How to get the nth Fibonacci number code in Java using recursion with memoization
import java.util.*;
public class fibonacci{
public static int fib(int n){
if(n==1){
return array[0];
}
// base cases
if(n==2){
return array[1];
}
else{
array[n-1] = fib(n-1) + fib(n-2);
return (array [n-1]);
}
}
public static void main(String args[]){
int n;
Scanner snr= new Scanner(System.in);
n=snr.nextInt();
snr.close();
array[0]=0;
array[1]=1;
System.out.println(fib(n));
// printing number in fibonacci series
}
static int array[]=new int[1000];
// Declaring global array large enough
}Time Complexity:
The time complexity for this approach is O( N ) which is linear time complexity, where n is the index of the nth Fibonacci number.
We need to find the previous two values for getting each value – but here we have already stored them in an array, so we need to call the function only once for all elements.
Space Complexity:
The space Complexity for this approach is O( N ) which is linear space complexity, where n is the index of the nth Fibonacci number.
We need to store only the values for each node and we have only N nodes.
Conclusion
In this article, we learned how to find the Fibonacci series in Java in four different ways, two each for the Bottom-Up approach and the Top-Bottom approach.
We've also learned that recursion with memoization is the most time and space-efficient way to get Fibonacci numbers.
In this article, we have discussed the space and time complexity of each approach along with their algorithms, advantages, and disadvantages.
Happy Learning and Coding!

