by Vikash Singh

How our startup switched from Unsupervised LDA to Semi-Supervised GuidedLDA

This is the story of how and why we had to write our own form of Latent Dirichlet Allocation (LDA). I also talk about why we needed to build a Guided Topic Model (GuidedLDA), and the process of open sourcing everything on GitHub.

What Is LDA (Topic Modeling)?

Lets say that you have a set of News Articles which were documents. By reading those articles you will be able to tell if they are about Sports, Politics or Science.

For the following titles you will agree that 1 and 5 are about Politics, 2 and 4 about Sports, and 3 and 6 about Science:

For a human being it’s not a challenge to figure out which topic a news article belongs to. But how can we teach a computer to understand the same topics?

This is where topic modeling comes into picture. Topic modeling is an unsupervised class of machine learning Algorithms. These models are generally good at grouping words together into topics. LDA is the most popular topic modeling technique.

Once we have the words grouped into topics, we can now see which group of words the news articles and document talks about. Then we can classify it into that group or topic.

As we can see, this new News Article talks about Nobel Prize. We can now predict that this document talks about Science topic.

Note: Words are not grouped directly into topics. Rather a probability is calculated such as “What is the probability of a word belonging to a topic?”.

It’s given by p(t|w). Or probability of topic t given word w. At it’s core it’s just Bayesian_probability.

I would love to talk more about it, but don’t want to deviate from the core problem. If you are interested, you can read more about it here.

So What Is Guided LDA?

Topic modeling is generally an unsupervised learning algorithm. We know that Space and Tech are topics of their own. But if we don’t get many articles about them or if they get mentioned together, they might get classified into one topic.

I ran into a similar problem recently. I work as a Data Scientist at Belong.co and Natural Language Processing is half of my work. Recently I was doing LDA topic modeling on our data corpus. Most of the topics came out as I was expecting them to. But some of the topics did not make sense.

A couple of the topics were overlapping and some of the topics which I was expecting to come out were not there. Something of this sort happened, Space and Tech got merged together.

In a supervised learning algorithm you can go back and debug where you went wrong in the decision making process. Perhaps you needed more features. Or more training data. Or maybe better loss function, metrics, and sampling.

But where to begin when the model is unsupervised? We decided to debug…

We found that the topics that were getting blended together didn’t have enough documents to stand out.

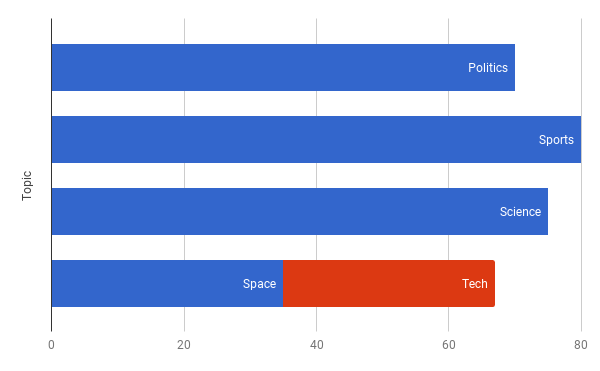
We decided to tell the model to keep Space and Tech separate. The idea was to set some seed words for Space and some seed words for Tech. Then guide the model to converge around those terms.

It was a simple and intuitive idea, but we couldn’t find any implementation of a GuidedLDA. There were very few papers which talked about guiding the LDA.

We referred to the Paper by Jagadeesh Jagarlamudi, Hal Daume III and Raghavendra Udupa Incorporating Lexical Priors into Topic Models. The paper talks about how the priors (in this case priors mean seeded words) can be set into the model to guide it in a certain direction. We will get into the details in a bit.

Once we made those changes, the model converged the way we wanted it to.

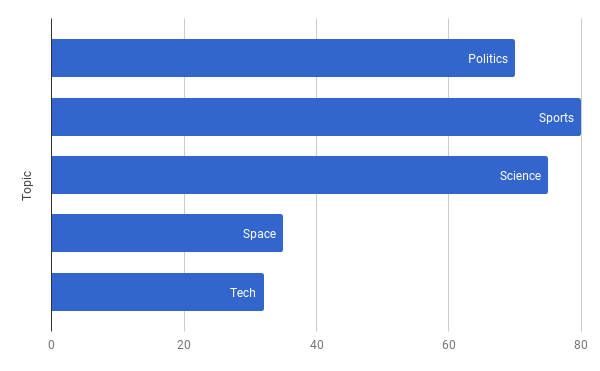
So How did we change LDA to GuidedLDA?

To explain this part, we will have to get into the details of how LDA works. I will try my best to keep it simple. If you don’t want to get into it, you can skip ahead to the Using GuidedLDA section.

The way regular LDA works is, first each word is randomly assigned to a topic. This initialization can be controlled with Dirichlet priors via the Alpha parameter. That’s where LDA (Latent Dirichlet Allocation) gets it’s name. This randomness could be uniform initialization if the alpha is large, or skewed initialization when the alpha is small. Let’s go ahead with uniform initialization for now.

The next step is to find out which term belongs to which topic. This is the topic modeling part of the algorithm. LDA goes for a very simple approach by finding the topic for one term at a time.

Say you want to find a topic for the term Blue Origin. The LDA will first assume that every other term in the corpus is assigned to the right topic. In the last step we had uniformly distributed each term in all topics, so we will assume that is the correct topic for those terms.

Then we compute which terms Blue Origin frequently comes along with. Then, which is the most common topic among those terms. We will assign Blue Origin to that topic.

Blue Origin will probably go near whichever topic SpaceX and NASA are in. Now you can see that NASA, SpaceX and Blue Origin are little closer to each other than they were before this step. Then we will move to the next term and repeat the process. We will repeat this entire process enough number of times needed to cause the model to converge.

The formula for this will be:
Probability of Blue Origin to fit in topic Z {0,1,2,..} when it occurs in a document is equal to the number of times Blue Origin is assigned to topic Z multiplied by the number of other words in that document that already belong to Z, divided by total the number of times any word is assigned to topic Z.

Here’s the actual formula:

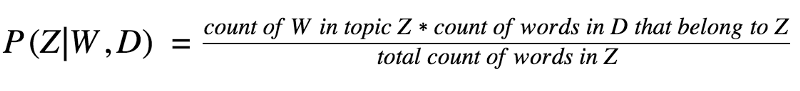
For each Document (D) and for each word (W) in that document, we will calculate the probability of that word belonging to each topic (Z).

for d in all_documents_D:    for w in all_words_W_in_d:        for z in all_topics_Z:            w_in_z = count(across all documents w belongs to z)            d_in_z = count(in d all words that belong to z)            tokens_in_z = count(all assignments in z)            p(z| w, d) = w_in_z * d_in_z / tokens_in_z        # so w belong to max p(z)        # whichever topic the probability was maximum for w        w_z = max(p(z| w, d))

The initial results will be wrong. But we will run this entire process multiple times and with each iteration they will get better. Over time they will converge to form word topic distribution.

What changes when we seed the documents?

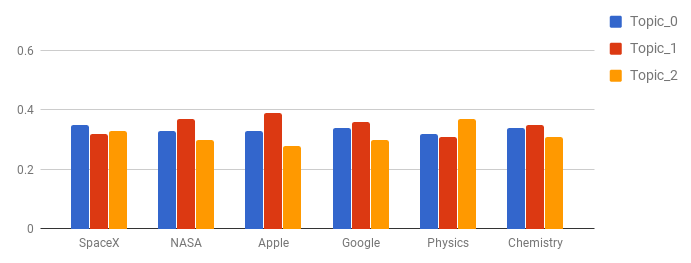
Say we want to seed SpaceX, NASA to converge towards topic_0. During initialization we can give some extra boost to SpaceX and NASA to lie in this specific topic.

We can control this parameter of how much extra boost should be given to a term. In our algorithm we call it seed_confidence and it can range between 0 and 1. With a seed_confidence of 0.1 you can bias the seeded words by 10% more towards the seeded topics.

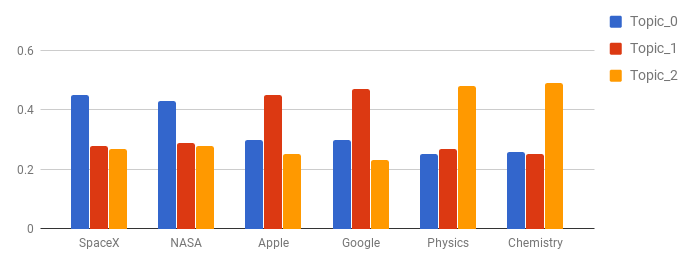
In the above shown initialization, NASA and SpaceX are being seeded for Topic_0, Apple and Google for Topic_1, and Physics and Chemistry for Topic_2.

Now when we run the above process we will have higher count for seeded words belonging to the seeded topics. The formula will remain the same for GuidedLDA and the convergence will change towards the seeded topics.

# for seeded words belonging to seeded topics# this count will be higher now for seeded z.

w_in_z = count(across all documents w belongs to z)

# Thus probability of p belonging to seeded z will be higher

p(z| w, d) ∝ w_in_z

Hence guiding the LDA. Or GuidedLDA.

We tried a lot of different approaches before finally making this one work.

Using GuidedLDA

GuidedLDA is a python library that I have open sourced on GitHub repo.

You can install it with a simple pip install:

pip install guidedlda

The code to use it is fairly simple. Create a dictionary for seed_topics with word_id to topic_id map. And pass it to the model.fit() method.

1. seed_confidence can vary between 0 to 1.
2. seed_topics is the dictionary {word_id to topic_id}
3. X is the document term matrix.

seed_topics = {    'NASA': 0, 'SpaceX': 0,    'Apple': 1, 'Google': 1,    'Physics': 2, 'Chemistry': 2,}model.fit(X, seed_topics=seed_topics, seed_confidence=0.15).

Documentation for GuidedLDA is linked here.

Credits

A major part of the code is borrowed from python LDA library.

A huge shoutout to the authors of that library : Allen Riddell and Tim Hopper.

Special thanks to Vinodh Ravindranath, who mentored me throughout the project.

By using GuidedLDA we were able to separate out topics which had smaller representation in the corpus and guide the classification of documents.

We have seen success with this model in production. But still, the Algorithm and the implementation is at an early stage. We request you to try it out and share your thoughts, experiments and results. Would love to hear from you.