by Shashi Kumar Raja

Intro to property-based testing in Python

In this article we will learn a unique and effective approach to testing called property-based testing. We will use Python , pytest and Hypothesis to implement this testing approach.

The article is going to use basic pytest concepts to explain property-based testing. I recommend that you read this article to quickly brush up your pytest knowledge.

We will start with the conventional unit/functional testing method known as example-based testing — which most of us use. We try to find its shortcomings, and then move to the property-based approach to remove those shortcomings.

Every great magic trick consists of three parts or acts. The first part is called “The Pledge”. The magician shows you something ordinary: a deck of cards, a bird or a man. He shows you this object. Perhaps he asks you to inspect it to see if it is indeed real, unaltered, normal. But of course…it probably isn’t.

Part 1: Example-based testing

The approach of example-based testing has the following steps:

• given a test input I
• when passed to function under test
• should return an output O

So, basically we give a fixed input and expect a fixed output.

To understand this concept in layman’s terms:

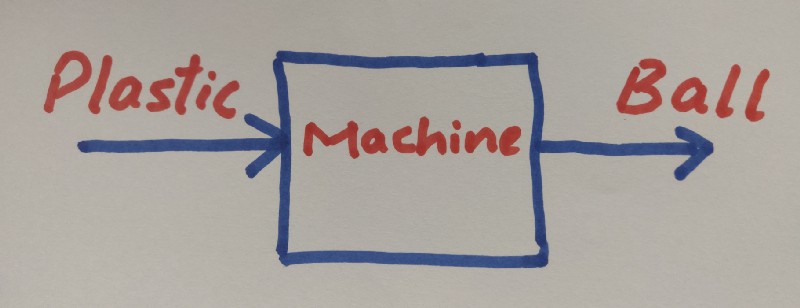
Assume we have a machine which takes plastic of any shape and any colour as input and produces a perfectly round plastic ball of the same colour as output.

Now, to test this machine using example-based testing, we will follow below approach:

1. take a blue-coloured raw plastic (fixed test data)
2. feed the plastic to machine
3. expect a blue-coloured plastic ball as output(fixed test output)

Let’s see the same approach in a programmatic way.

Prerequisite: make sure you have Python (ver 2.7 or above) and pytest installed.

Create a directory structure like this:

- demo_tests/    - test_example.py

We will write one small function sum inside file test_example.py . This accepts two numbers — num1 and num2 — as parameters and returns the addition of both numbers as result.

def sum(num1, num2):    """It returns sum of two numbers"""    return num1 + num2

Now, lets write a test to test this sum function following the conventional method.

import pytest

#make sure to start function name with testdef test_sum():    assert sum(1, 2) == 3

Here you can see that, we are passing the two values 1 and 2 and expecting the sum to return 3.

Run the tests by traversing to demo_tests folder and then running following command:

pytest test_example.py -v

Is this test enough to verify the functionality of the sum function?

You might be thinking, of course not. We will write more tests using the pytest parametrize feature which will execute this test_sum function for all the given values.

import pytest

@pytest.mark.parametrize('num1, num2, expected',[(3,5,8),              (-2,-2,-4), (-1,5,4), (3,-5,-2), (0,5,5)])def test_sum(num1, num2, expected):        assert sum(num1, num2) == expected

Using five tests has given more confidence about the functionality. All of them passing feels like bliss.

But, if you look more closely we are doing the same thing we did above but for more number of values. We are still not covering several of the edge cases.

So, we have discovered the first pain point with this method of testing:

Issue 1: Test exhaustiveness depends on the person writing the test

They may choose to write 5 or 50 or 500 test cases but still remain unsure whether they have safely covered most, if not all, the edge cases.

This brings us to our second pain point:

Issue 2 — Non-robust tests due to unclear/ambiguous requirement understanding

When we were told to write our sum function, what specific details were conveyed?

Were we told:

• what kind of input our function should expect?
• how our function should behave in unexpected input scenarios?
• what kind of output our function should return?

To be more precise, if you consider the sum function we have written above:

• do we know if num1, num2 should be an int or float? Can they also be sent as type string or any other data type?
• what is the minimum and maximum value of num1 and num2 that we should support?
• how should the function behave if we get null inputs?
• should the output returned by the sum function be int or float or string or any other data type?
• in what scenarios should it display error messages?

Also, the worst case scenario of the above test case writing approach is that these test cases can be fooled to pass by buggy functions.

Let’s re-write our sum function in a way that errors are introduced but the tests which we have written so far still passes.

def sum(num1, num2):    """Buggy logic"""       if num1 == 3 and num2 == 5:        return 8    elif num1 == -2 and num2  == -2 :        return -4    elif num1 == -1 and num2 == 5 :        return 4    elif num1 == 3 and num2 == -5:        return -2    elif num1 == 0 and num2 == 5:        return 5

Now let’s dive into property-based testing to see how these pain points are mitigated there.

The second act is called “The Turn”. The magician takes the ordinary something and makes it do something extraordinary. Now you’re looking for the secret… but you won’t find it, because of course you’re not really looking. You don’t really want to know. You want to be fooled.

Part 2: Property-based testing

Intro and test data generation

Property-based testing was first introduced by the QuickCheck framework in Haskell. As per fast-check’s documentation, which is another property based testing library-

Property based testing frameworks check the truthfulness of properties. A property is a statement like:

for all (x, y, …)

such as precondition(x, y, …) holds

property(x, y, …) is true.

To understand this let’s go back to our plastic ball generating machine example.

The property based testing approach of that machine will be:

1. take a huge selection of plastics as input (all(x, y, …))
2. make sure all of them are colored (precondition(x, y, …))
3. the output satisfies following property (property(x, y, …)) -

• output is round/spherical in shape
• output is colored
• color of the output is one of the colors present in color band

Notice how from fixed values of input and output we have generalized our test data and output in such a way that the property should hold true for all the valid inputs. This is property-based testing.

Also, notice that when thinking in terms of properties we have to think harder and in a different way. Like when we came up with the idea that since our output is a ball it should be round in shape, another question will strike you - whether the ball should be hollow or solid?

So, by making us think harder and question more about the requirement, the property-based testing approach is making our implementation of the requirement robust.

Now, let’s return to our sum function and test it by using the property-based approach.

The first question which arises here is: what should be the input of the sum function?

For the scope of this article we will assume that any pair of integers from the integer set is a valid input.

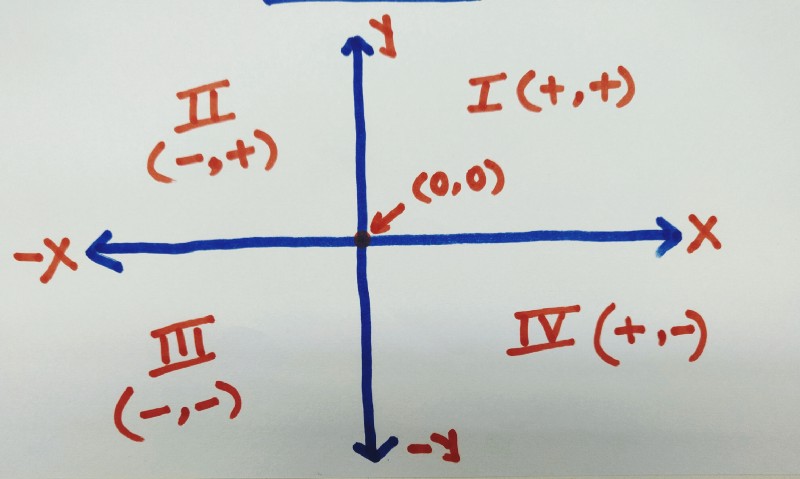
So, any set of integer values lying in the above coordinate system will be a valid input to our function.

The next question is: how to get such input data?

The answer to this is: a property-based testing library provides you the feature to generate huge set of desired input data following a precondition.

In Python, Hypothesis is a property-testing library which allows you to write tests along with pytest. We are going to make use of this library.

The entire documentation of Hypothesis is beautifully written and available ➡️ here and I recommend you to go through it.

To install Hypothesis:

pip install hypothesis

and we are good to use hypothesis with pytest.

Now, let’s rewrite test_sum function — which we wrote earlier — with new data sets generated by Hypothesis.

from hypothesis import given

import hypothesis.strategies as st

import pytest

@given(st.integers(), st.integers())def test_sum(num1, num2):    assert sum(num1, num2) == num1 + num2

• The first line simply imports given from Hypothesis. The @given decorator takes our test function and turns it into a parametrized one. When called, this will run the test function over a wide range of matching data. This is the main entry point to Hypothesis.
• The second line imports strategies from Hypothesis. strategies provides the feature to generate test data. Hypothesis provides strategies for most built-in types with arguments to constrain or adjust the output. As well, higher-order strategies can be composed to generate more complex types.
• You can generate any or mix of the following things using strategies:

'nothing','just', 'one_of','none','choices', 'streaming','booleans', 'integers', 'floats', 'complex_numbers', 'fractions','decimals','characters', 'text', 'from_regex', 'binary', 'uuids','tuples', 'lists', 'sets', 'frozensets', 'iterables','dictionaries', 'fixed_dictionaries','sampled_from', 'permutations','datetimes', 'dates', 'times', 'timedeltas','builds','randoms', 'random_module','recursive', 'composite','shared', 'runner', 'data','deferred','from_type', 'register_type_strategy', 'emails'

• Here we have generated integers()set using strategies and passed it to @given.
• So, our test_sum function should run for all the iterations of given input.

Let’s run it and see the result.

You might be thinking, I can’t see any difference here. What’s so special about this run?

Well, to see the magical difference, we need to run our test by setting the verbose option. Don’t confuse this verbose with the -v option of pytest.

from hypothesis import given, settings, Verbosity

import hypothesis.strategies as stimport pytest

@settings(verbosity=Verbosity.verbose)@given(st.integers(), st.integers())def test_sum(num1, num2):    assert sum(num1, num2) == num1 + num2

settings allows us to tweak the default test behavior of Hypothesis.

Now let’s re-run the tests. Also include -s this time to capture the stream output in pytest.

pytest test_example.py -v -s

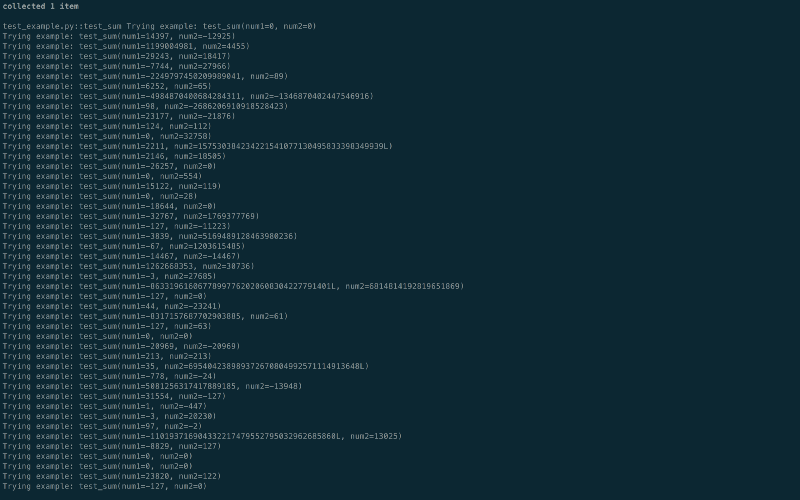
Look at the sheer number of test-cases generated and run. You can find all sorts of cases here, such as 0, large numbers, and negative numbers.

You might be thinking, it’s impressive, but I can’t find my favorite test case pair (1,2 ) here. What if I want that to run?

Well, fear not, Hypothesis allows you to run a given set of test cases every time if you want by using the @example decorator.

from hypothesis import given, settings, Verbosity, example

import hypothesis.strategies as stimport pytest

@settings(verbosity=Verbosity.verbose)@given(st.integers(), st.integers())@example(1, 2)def test_sum(num1, num2):    assert sum(num1, num2) == num1 + num2

Also, notice that each run will always generate a new jumbled up test case following the test generation strategy, thus randomizing the test run.

So, this solves our first pain point- the exhaustiveness of test cases.

Thinking hard to come up with properties to test

So far, we saw one magic of property-based testing which generates desired test data on the fly.

Now let’s come to the part where we need to think hard and in a different way to create such tests which are valid for all test inputs but unique to sum function.

1 + 0 = 10 + 1 = 15 + 0 = 5-3 + 0 = -38.5 + 0 = 8.5

Well, that’s interesting. It seems like adding 0 to a number results in the same number as sum. This is called the identity property of addition.

Let’s see one more:

2 + 3 = 53 + 2 = 5

5 + (-2) = 3-2 + 5 = 3

It looks like we found one more unique property. In addition the order of parameters doesn’t matter. Placed left or right of the + sign they give the same result. This is called the commutative property of addition.

There is one more, but I want you to come up with it.

Now, we will re-write our test_sum to test these properties:

from hypothesis import given, settings, Verbosity

import hypothesis.strategies as stimport pytest

@settings(verbosity=Verbosity.verbose)@given(st.integers(), st.integers())def test_sum(num1, num2):    assert sum(num1, num2) == num1 + num2

    # Test Identity property    assert sum(num1, 0) = num1     #Test Commutative property      assert sum(num1, num2) == sum(num2, num1)

Our test is now exhaustive — we have also converted the tests to make them more robust. Thus, we solved our second pain point: non-robust test cases.

Just for curiosity’s sake, let’s try to fool this test with that buggy code we used before.

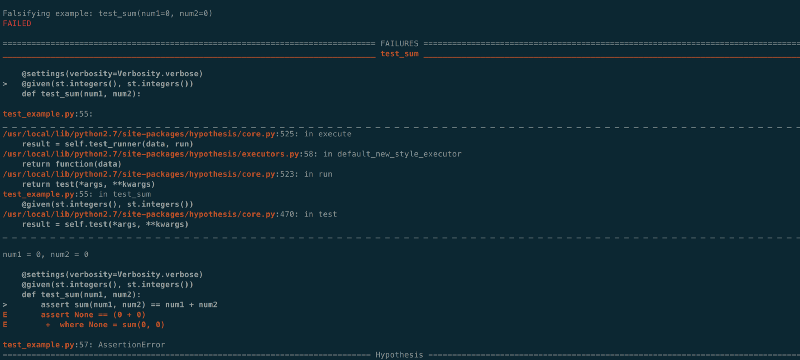
As an old proverb says- fool me once, shame on you, fool me twice, shame on me.

You can see that it caught an error. Falsifying example: test_sum(num1=0, num2=0). It simply means that our expected property didn't hold true for these pairs of test cases, thus the failure.

But you wouldn’t clap yet. Because making something disappear isn’t enough; you have to bring it back. That’s why every magic trick has a third act, the hardest part, the part we call “The Prestige”.

Part 3: Shrinking failures

Shrinking is the process by which Hypothesis tries to produce human-readable examples when it finds a failure. It takes a complex example and turns it into a simpler one.

To demonstrate this feature, let’s add one more property to our test_sum function which says num1 should be less than or equal to 30.

from hypothesis import given, settings, Verbosity

import hypothesis.strategies as stimport pytest

@settings(verbosity=Verbosity.verbose)@given(st.integers(), st.integers())def test_sum(num1, num2):    assert sum(num1, num2) == num1 + num2

    # Test Identity property    assert sum(num1, 0) = num1     #Test Commutative property      assert sum(num1, num2) == sum(num2, num1)    assert num1 <= 30

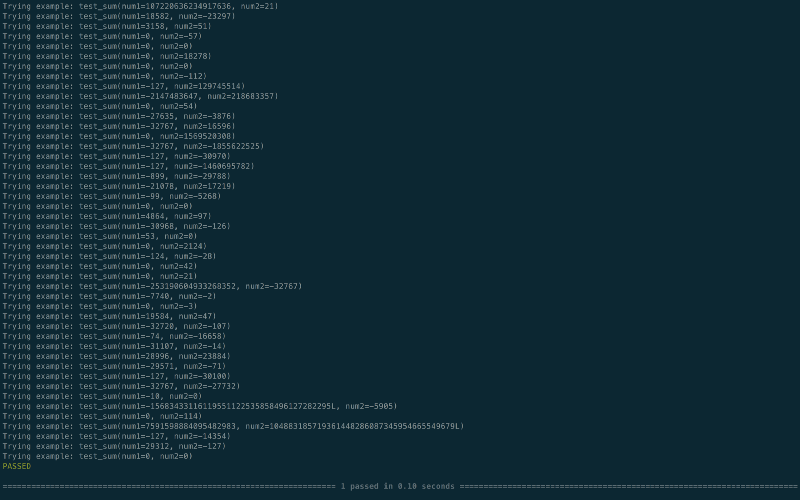
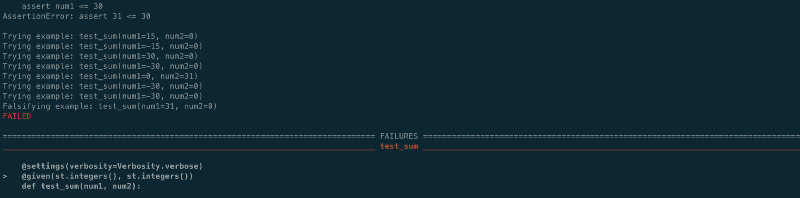
After running this test, you will get an interesting output log on the terminal here:

collected 1 item

test_example.py::test_sum Trying example: test_sum(num1=0, num2=-1)Trying example: test_sum(num1=0, num2=-1)Trying example: test_sum(num1=0, num2=-29696)Trying example: test_sum(num1=0, num2=0)Trying example: test_sum(num1=-1763, num2=47)Trying example: test_sum(num1=6, num2=1561)Trying example: test_sum(num1=-24900, num2=-29635)Trying example: test_sum(num1=-13783, num2=-20393)

#Till now all test cases passed but the next one will fail

Trying example: test_sum(num1=20251, num2=-10886)assert num1 <= 30AssertionError: assert 20251 <= 30

#Now the shrinking feature kicks in and it will try to find the simplest value for which the test still fails

Trying example: test_sum(num1=0, num2=-2)Trying example: test_sum(num1=0, num2=-1022)Trying example: test_sum(num1=-165, num2=-29724)Trying example: test_sum(num1=-14373, num2=-29724)Trying example: test_sum(num1=-8421504, num2=-8421376)Trying example: test_sum(num1=155, num2=-10886)assert num1 <= 30AssertionError: assert 155 <= 30

# So far it has narrowed it down to 155

Trying example: test_sum(num1=0, num2=0)Trying example: test_sum(num1=0, num2=0)Trying example: test_sum(num1=64, num2=0)assert num1 <= 30AssertionError: assert 64 <= 30

# Down to 64

Trying example: test_sum(num1=-30, num2=0)Trying example: test_sum(num1=0, num2=0)Trying example: test_sum(num1=0, num2=0)Trying example: test_sum(num1=31, num2=0)

# Down to 31

Trying example: test_sum(num1=-30, num2=0)Falsifying example: test_sum(num1=31, num2=0)FAILED

# And it finally concludes (num1=31, num2=0) is the simplest test data for which our property doesn't hold true.

One more good feature — its going to remember this failure for this test and will include this particular test case set in the future runs to make sure that the same regression doesn’t creep in.

This was a gentle introduction to the magic of property based testing. I recommend all of you try this approach in your day to day testing. Almost all major programming languages have property based testing support.

You can find the entire code used here in my ? github repo.

If you liked the content show some ❤️