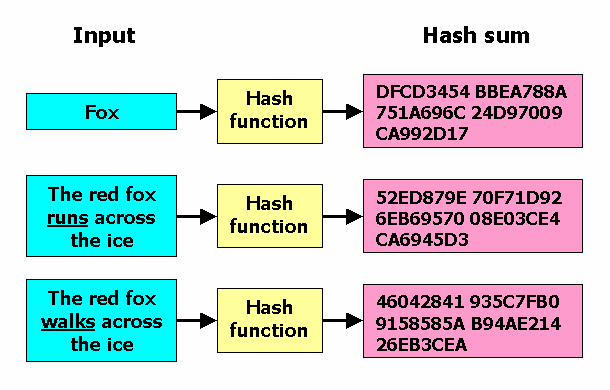
What's a hash function?
A hash function takes an input value (for instance, a string) and returns a fixed-length value. An ideal hash function has the following properties:
- it is very fast
- it can return an enormous range of hash values
- it generates a unique hash for every unique input (no collisions)
- it generates dissimilar hash values for similar input values
- generated hash values have no discernable pattern in their distribution
No ideal hash function exists, of course, but each aims to operate as close to the ideal as possible. Given that (most) hash functions return fixed-length values and the range of values is therefore constrained, that constraint can practically be ignored. The number of possible values that can be returned by a a 256-bit hash function, for instance, is roughly the same as the number of atoms in the universe.
Ideally, a hash function returns practically no collisions – that is to say, no two different inputs generate the same hash value. This is particularly import for cryptographic hash functions: hash collisions are considered a vulnerability.
Finally, a hash function should generate unpredictably different hash values for any input value. For example, take the following two very similar sentences:
1. "The quick brown fox."
2. "The quick brown fax."
We can compare the MD5 hash values generated from each of the two sentences:
1. 2e87284d245c2aae1c74fa4c50a74c77
2. c17b6e9b160cda0cf583e89ec7b7fc22
Two very dissimilar hashes were generated for two similar sentences, which is a property useful both for validation and cryptography. This is a corollary of distribution: the hash values of all inputs should be spread evenly and unpredictably across the whole range of possible hash values.
Common hash functions
There are several hash functions that are widely used. All were designed by mathematicians and computer scientists. Over the course of further research, some have been shown to have weaknesses, though all are considered good enough for noncryptographic applications.
MD5
The MD5 hash function produces a 128-bit hash value. It was designed for use in cryptography, but vulnerabilities were discovered over the course of time, so it is no longer recommended for that purpose. However, it is still used for database partitioning and computing checksums to validate files transfers.
SHA-1
SHA stands for Secure Hash Algorithm. The first version of the algorithm was SHA-1, and was later followed by SHA-2 (see below).
Whereas MD5 produces a 128-bit hash, SHA1 generates 160-bit hash (20 bytes). In hexadecimal format, it is an integer 40 digits long. Like MD5, it was designed for cryptology applications, but was soon found to have vulnerabilities also. As of today, it is no longer considered to be any less resistant to attack than MD5.
SHA-2
The second version of SHA, called SHA-2, has many variants. Probably the one most commonly used is SHA-256, which the National Institute of Standards and Technology (NIST) recommends using instead of MD5 or SHA-1.
The SHA-256 algorithm returns hash value of 256-bits, or 64 hexadecimal digits. While not quite perfect, current research indicates it is considerably more secure than either MD5 or SHA-1.
Performance-wise, a SHA-256 hash is about 20-30% slower to calculate than either MD5 or SHA-1 hashes.
SHA-3
This hash method was developed in late 2015, and has not seen widespread use yet. Its algorithm is unrelated to the one used by its predecessor, SHA-2.
The SHA3-256 algorithm is a variant with equivalent applicability to that of the earlier SHA-256, with the former taking slightly longer to calculate than the later.
Using Hash Values for Validation
A typical use of hash functions is to perform validation checks. One frequent usage is the validation of compressed collections of files, such as .zip or .tar archive files.
Given an archive and its expected hash value (commonly referred to as a checksum), you can perform your own hash calculation to validate that the archive you received is complete and uncorrupted.
For instance, I can generate an MD5 checksum for a tar file in Unix using the following piped commands:
tar cf - files | tee tarfile.tar | md5sum -
To get the MD5 hash for a file in Windows, use the Get-FileHash PowerShell command:
Get-FileHash tarfile.tar -Algorithm MD5
The generated checksum can be posted on the download site, next to the archive download link. The receiver, once they have downloaded the archive, can validate that it came across correctly by running the following command:
echo '2e87284d245c2aae1c74fa4c50a74c77 tarfile.tar' | md5sum -c
where 2e87284d245c2aae1c74fa4c50a74c77 is the generated checksum that was posted. Successful execution of the above command will generate an OK status like this:
echo '2e87284d245c2aae1c74fa4c50a74c77 tarfile.tar' | md5sum -ctarfile.tar: OK