by Festus K. Yangani
A Beginners Guide to Big O Notation
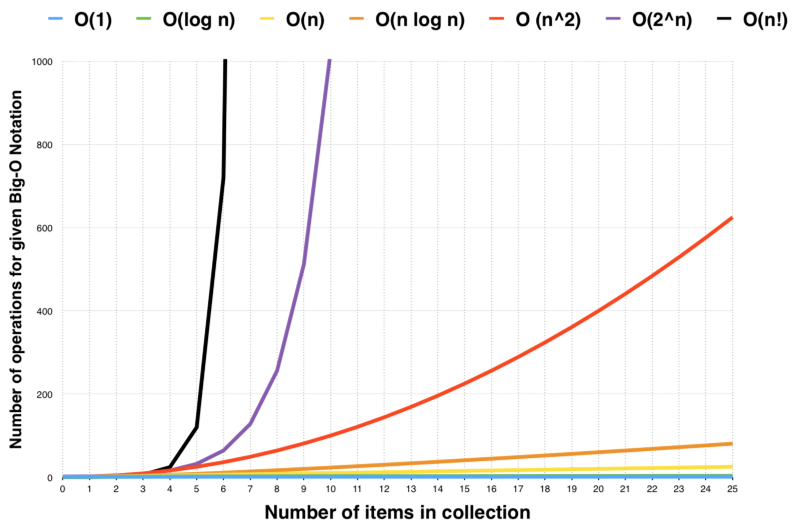
Big O Notation is a way to represent how long an algorithm will take to execute. It enables a software Engineer to determine how efficient different approaches to solving a problem are.
Here are some common types of time complexities in Big O Notation.
- O(1) - Constant time complexity
- O(n) - Linear time complexity
- O(log n) - Logarithmic time complexity
- O(n^2) - Quadratic time complexity
Hopefully by the end of this article you will be able to understand the basics of Big O Notation.
O(1) — Constant Time
Constant time algorithms will always take same amount of time to be executed. The execution time of these algorithm is independent of the size of the input. A good example of O(1) time is accessing a value with an array index.
var arr = [ 1,2,3,4,5];arr[2]; // => 3Other examples include: push() and pop() operations on an array.
O(n) - Linear time complexity
An algorithm has a linear time complexity if the time to execute the algorithm is directly proportional to the input size n. Therefore the time it will take to run the algorithm will increase proportionately as the size of input n increases.
A good example is finding a CD in a stack of CDs or reading a book, where n is the number of pages.
Examples in of O(n) is using linear search:
//if we used for loop to print out the values of the arraysfor (var i = 0; i < array.length; i++) { console.log(array[i]);}var arr1 = [orange, apple, banana, lemon]; //=> 4 stepsvar arr2 = [apple, htc,samsung, sony, motorola]; //=> 5 stepsO(log n) - Logarithmic time complexity
An algorithm has logarithmic time complexity if the time it takes to run the algorithm is proportional to the logarithm of the input size n. An example is binary search, which is often used to search data sets:
//Binary search implementationvar doSearch = function(array, targetValue) { var minIndex = 0; var maxIndex = array.length - 1; var currentIndex; var currentElement; while (minIndex <= maxIndex) { currentIndex = (minIndex + maxIndex) / 2 | 0; currentElement = array[currentIndex]; if (currentElement < targetValue) { minIndex = currentIndex + 1; } else if (currentElement > targetValue) { maxIndex = currentIndex - 1; } else { return currentIndex; } } return -1; //If the index of the element is not found.};var numbers = [11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33];doSearch(numbers, 23) //=>; 6Other examples of logarithmic time complexity include:
Example 1;for (var i = 1; i < n; i = i * 2) console.log(i);}Example 2;for (i = n; i >= 1; i = i/2) console.log(i);}O(n^2) - Quadratic time complexity
An algorithm has quadratic time complexity if the time to execution it is proportional to the square of the input size. A good example of this is checking to see whether there are any duplicates in a deck of cards.
You will encounter quadratic time complexity in algorithms involving nested iterations, such as nested for loops. In fact, the deeper nested loops will result in O(n^3), O(n^4), etc.
for(var i = 0; i < length; i++) { //has O(n) time complexity for(var j = 0; j < length; j++) { //has O(n^2) time complexity // More loops? }}Other examples of quadratic time complexity include bubble sort, selection sort, and insertion sort.
This article only scratches the surface of Big O Notation. If you would like to understand more about Big O Notation, I recommend checking out the Big-O Cheat Sheet.