In Computer Science, Prim’s algorithm helps you find the minimum spanning tree of a graph. It is a greedy algorithm – meaning it selects the option available at the moment.
In this article, I’ll show you the pseudocode representation of Prim’s algorithm. But before that, let’s take a deeper look at what Prim’s algorithm is.
What We'll Cover
- What is Prim’s Algorithm?
- How to Implement Prim’s Algorithm
- Pseudocode Example of Prim’s Algorithm
- How to Implement Prim’s Algorithm in JavaScript Using the Pseudocode
- Conclusion
What is Prim’s Algorithm?
Prim’s algorithm is a type of greedy algorithm for finding the minimum spanning tree (MST) of an undirected and weighted graph.
A minimum spanning tree (MST) is the subset of the edges of a graph that connects all the vertices (the point where the sides meet) together so that the total weight of the edges is minimized without forming a cycle.
So, bear in mind that if you’re finding the MST of a graph with Prim’s algorithm, there must be no cycle. That is, if A links to B and B links to C, C cannot link to A again because that would make a cycle. I prepared some infographics with explanations that will help you grasp it better in the next sections of this article.
The total weight of the edges is also commonly referred to as cost. And one of the goals of Prim’s algorithm is to get the minimum cost tree that covers the vertices in the graph without leaving any of them behind.
So, that’s another thing to bear in mind – all the vertices must be involved in getting the minimum spanning tree (MST).
Prim’s algorithm is also called Jarník's algorithm because it was initially developed by Czech Mathematician Vojtěch Jarník in 1930. It was later rediscovered and published by Robert C. Prim in 1957 – hence the name Prim’s algorithm.
Prim’s algorithm works by starting from an arbitrary vertex, adding the minimum weight edge that connects the tree to a new vertex, and repeating this process until all vertices have been included in the tree.
How to Implement Prim’s Algorithm
To implement Prim’s algorithm in finding the minimum spanning tree of a graph, here are the three things to bear in mind:
- all the vertices of the graph must be included
- the vertex with the minimum weight must be selected first. You’ll also hear some people refer to that weight as distance, but let’s keep calling it weight.
- all the vertices must be connected
- there must be no cycle
Consider the graph below:
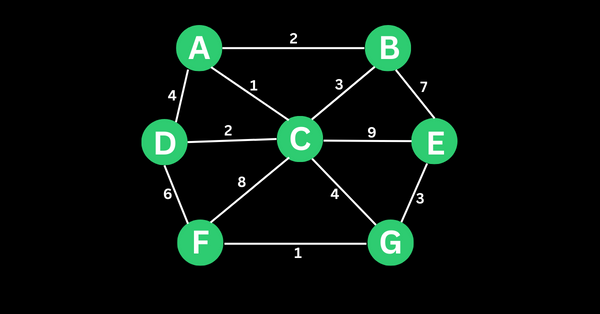
You have to start by choosing an arbitrary vertex as the starting point and adding it to the tree.
For the next step, you have to select the edge with the minimum weight that connects a vertex in the tree to a vertex not yet in the tree, and then add the new vertex to the tree.
Choosing D as the starting vertex resulted in this:
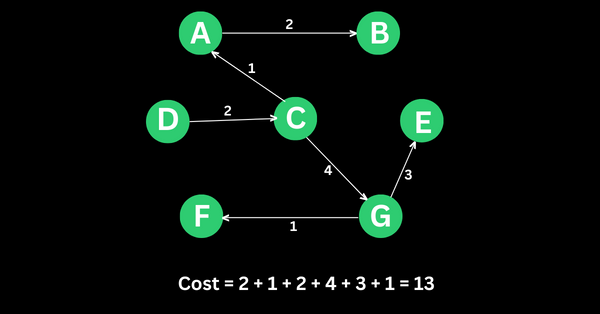
This is how it happened:
-
Dwas the starting point -
the next minimum weight connected to
Dis2– the line betweenDandC. So, I chose it. -
looking at vertex
C, the next minimum weight to it is1– the line betweenCandA. So, I chose it as the next one -
looking at
A, lines2and4are connected to it. We cannot choose4because it’s bigger than2and it’ll lead us back to the starting pointD. So, we have to choose2– the line connecting verticesAandB. -
looking at
B, line3connects it toCand line7connects it toE. We cannot choose line3because that will form a cycle betweenC,A, andB. We also should think twice before choosing line 7 because it’s a big number. There’s a line4connectingCtoG, so, I chose it -
On the vertex
G, there’s a connection toFwith line1and line3toE, so I’ll choose the minimum weight which is1 -
At this point,
Eis the only vertex not connected yet. It’s possible to connect it because it won’t form a cycle at any point. So, I connected it.
Here's the step-by-step connection:
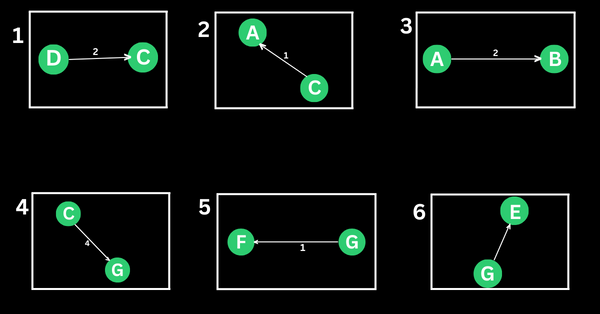
Again, this is what all of the points above lead to:
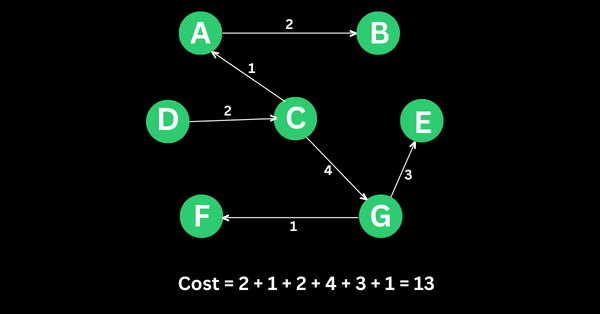
The cost is the sum of all the weights connected to the vertices. That’s how I got 13.
This process continues until all the vertices have been added to the tree. It doesn’t leave any of them behind and forms no cycle.
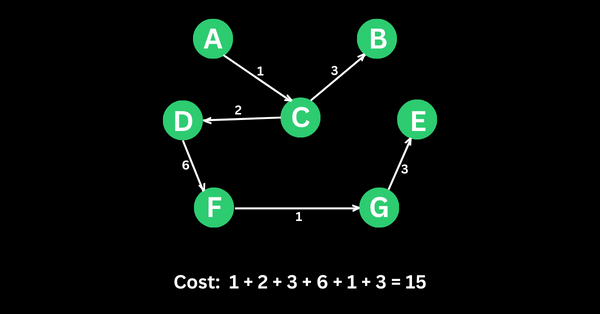
You can make any of the vertices the starting point. This is the result if I start from vertex A:
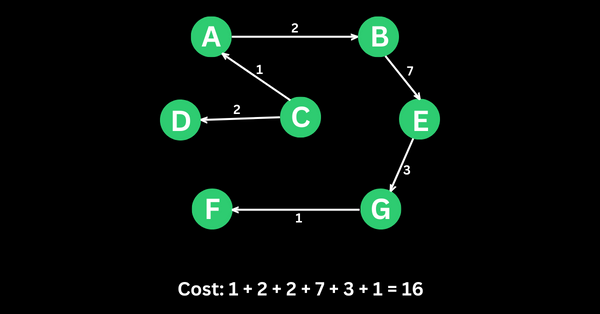
And this is the result if I start from vertex C:
Pseudocode Example of Prim’s Algorithm
Below is some pseudocode for the implementation of Prim’s algorithm. I have also included comments so you can keep track of things as they happen:
prim(graph):
# Initialize an empty set to hold the vertices in the minimum spanning tree
mst = empty set
# Select the first vertex to start the tree
startVertex = first vertex in graph
mst.add(startVertex)
# Initialize the set of edges to consider
edges = edges connected to startVertex
# Iterate until all vertices are in the minimum spanning tree
while mst has fewer vertices than graph:
# Find the minimum edge in the set of edges
minEdge, minWeight = findMinEdge(edges)
# Add the vertex to the minimum spanning tree
mst.add(minEdge)
# Add the edges connected to the vertex to the set of edges to consider
for edge in edges connected to minEdge:
if edge is not in mst:
edges.add(edge)
# Remove the minimum edge from the set of edges to consider
edges.remove(minEdge)
# Return the minimum spanning tree as an array
return mst as an array
How to Implement Prim’s Algorithm in JavaScript Using the Pseudocode
Using that pseudocode, you can implement Prim’s algorithm in JavaScript this way:
// Define a graph as an adjacent list
const graph = {
'A': {'B': 4, 'C': 2},
'B': {'A': 4, 'C': 1, 'D': 5},
'C': {'A': 2, 'B': 1, 'D': 8, 'E': 10},
'D': {'B': 5, 'C': 8, 'E': 2},
'E': {'C': 10, 'D': 2}
};
// Find the minimum edge in the edge list
function findMinEdge(edges) {
let minEdge = null;
let minWeight = Infinity;
for (const [v, weight] of Object.entries(edges)) {
if (weight < minWeight) {
minEdge = v;
minWeight = weight;
}
}
return [minEdge, minWeight];
}
// Find the minimum spanning tree using Prim's algorithm
function prim(graph) {
// Initialize an empty set to hold the vertices in the MST
const mst = new Set();
// Select the first vertex to start the tree
const startVertex = Object.keys(graph)[0];
mst.add(startVertex);
// Initialize the set of edges to consider
const edges = graph[startVertex];
// Iterate over the graph object until all vertices are in the MST
while (mst.size < Object.keys(graph).length) {
// Find the minimum edge in the set of edges
const [minEdge, minWeight] = findMinEdge(edges);
// Add the vertex to the MST
mst.add(minEdge);
// Add the edges connected to the vertex to the set of edges to consider
for (const [v, weight] of Object.entries(graph[minEdge])) {
if (!mst.has(v)) {
edges[v] = weight;
}
}
// Remove the minimum edge from the set of edges to consider
delete edges[minEdge];
}
// Return the MST as an array
return Array.from(mst);
}
// Call the prim function with the graph object
const minimumSpanningTree = prim(graph);
// Log the result to the console
console.log(minimumSpanningTree);
// Result: ['A', 'C', 'B', 'D', 'E']
Conclusion
Prim’s algorithm is a fun and useful algorithm used in everyday life to solve problems. That’s why this article was dedicated to showing you what it is and a pseudocode example with which you can implement it in any language.
If you are wondering what you can use Prim’s algorithm for, here are some of its applications:
- designing transportation networks
- building phylogenetic trees in bioinformatics
- segmenting images based on color and pixel intensity
- grouping similar objects together in clustering algorithms
Thank you for reading.