Python VS C++ Time Complexity Analysis

Speed is important in programming languages, and some execute much faster than others.

For example, you might know that C++ is faster than Python. So why is this the case?

Well, C++ is a language that uses a compiler, not to mention it is a much lower-level programming language than Python. That is to say, C++ provides much less abstraction from a computer's instruction set and architecture.

On the other hand, Python is an interpretated language, which just means that every line of the program is evaluated as the program is running.

But, how much faster IS C++ compared to Python? In this article you will see 3 algorithms and how they perform in C++ and Python. These algorithms are from "Data Structures and Algorithms Using C++" by Michael T. Goodrich.

Note: The computer I ran these tests on was an Acer Swift 3. The CPU was a Ryzen 7 7500U with Radeon Graphics 1.80Gz. Along with 8GB of RAM, running Windows 10 Home.

You will be looking at these algorithms and their Big O Notation. Big O is a mathematical way of expressing the worst-case scenario of the time or space complexity of an algorithm.

The time complexity is the amount of time it takes for an algorithm to run, while the space complexity is the amount of space (memory) an algorithm takes up. Here is a graph to help explain Big O:

From now on, I'll refer to each algorithm as running with a certain time complexity.

For example, if I say an algorithm runs with a O(n) time complexity, this means that as the input grows, the time it takes for an algorithm to run is linear. If I say it runs with O(n^2) time complexity, this means that as the input grows, the time it takes for an algorithm to run is quadratic.

Performance of the 1st Algorithm:

Algorithm Ex1(A):
    Input: An array "A" storing n >= 1 integers.
    Output: The sum of the elements in A.
    
    s = A[0]
    for i = 1 to n - 1 do:
        s = s + A[i]
    return s

In Python, we can express this algorithm as:

def ex1(A):
	sum = A[0]
	for i in A:
		sum = sum + A[i]
	return sum
   

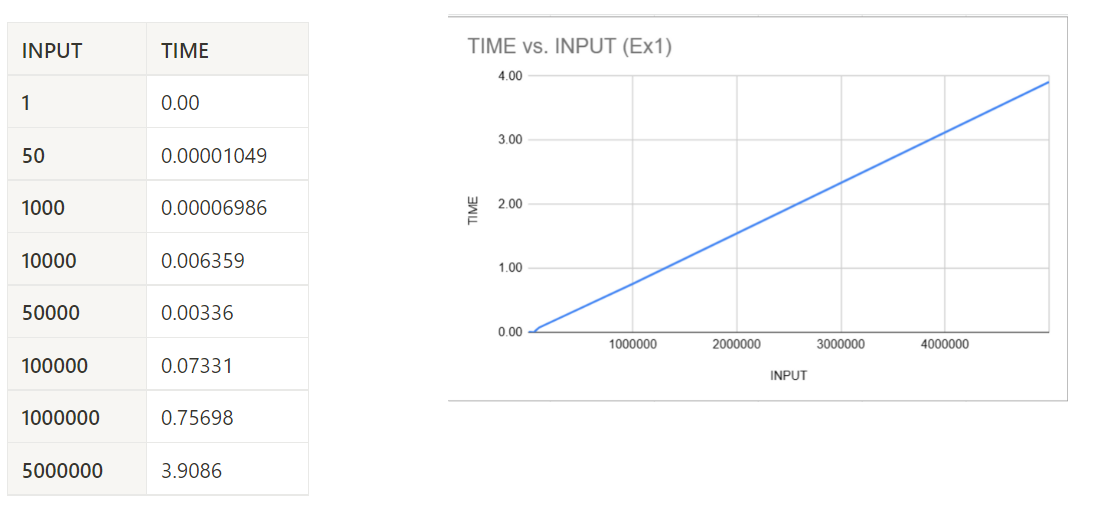
If you use inputs up to about 5 million you will see that this algorithm takes about 4 seconds to run with that large of an input.

Then you can compare this algorithm in C++, like this:

double ex1(double A[], size_t n)
{
    double sum = A[0];
    for(size_t i = 0; i < n; i++)
    {
        s = s + A[i];
    }
    return sum;
}

You may be wondering, what is size_t? size_t is an "unsigned integer". This just means that this variable does not have a sign. Which also just means that this variable is not negative.

In C++, we use size_t to keep track of positions in an array, since those positions cannot be negative (at least in C++, since in Python we can have negative indexes).

Now let's take a look at the running time of the first algorithm:

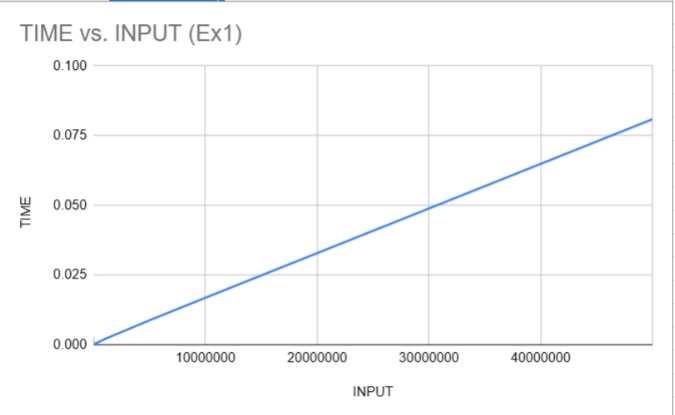
As you can see from these two charts, the time complexity seems to be linear. This means that the time complexity of this algorithm is O(n) – as the input size for A grows, the time it takes for this algorithm to run grows linearly.

But it is interesting to notice that for very large inputs of 5 million, C++ does not even break the 1 second mark. Whereas Python breaks the 3-4 second mark for inputs at about 5 million. Let's move on to our next algorithm.

Performance of the 2nd Algorithm:

Algorithm Ex3(A):
    Input: An array "A" storing n >= 1 integers.
    Output: The sum of the prefix sums in A.
    s = 0
    for i = 0 to n - 1 do:
        s = s + A[0]
        for j = 1 to i do:
            s = s + A[j]
    return s

Here, you can see that this algorithm has two for-loops. So, moving forward this is something to acknowledge when analyzing the time complexity.

In Python, you can express this algorithm like this:

def ex3(A):
    sum = 0
    for i in range(len(A)):
        sum = sum + A[i]
        for j in range(1, i):
            sum = sum + A[j]
    return sum

Let's also use inputs all the way up to 70,000. Then we will record the times and chart the data like so:

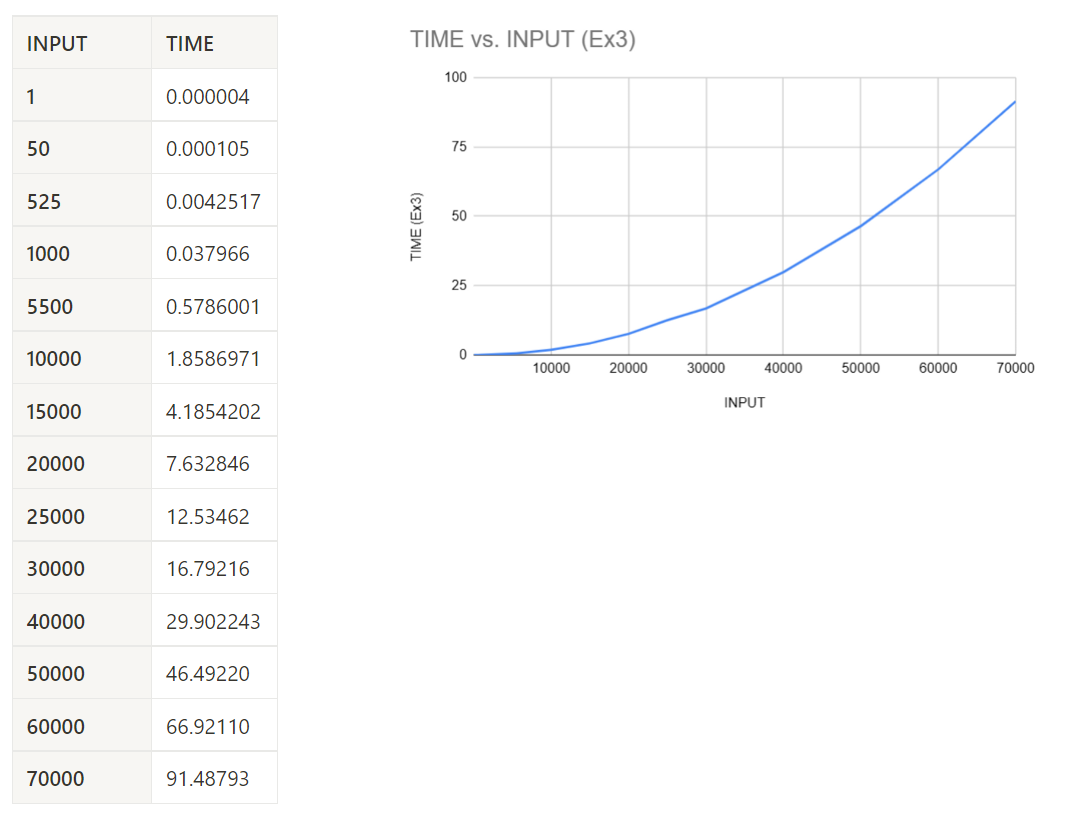
These results are much different from our previous charts from algorithm 1. Something to point out is that with an input of 70,000, this algorithm takes a whopping 91 seconds in Python. Thats a long time!

Also, when I tried to run inputs higher than 70,000, my computer started to become unresponsive. Yikes.

Let's take a look at this algorithm in C++:

double ex3(double A[], size_t n)
{
    double s = 0;
    for(size_t i = 0; i < n; i++)
    {
        s = s + A[i];
        for(size_t j = 1; j < i; j++)
        {
            s = s + A[j];
        }
    }
    return s;
}

For the C++ code I was able to increase the input size to ~90,000.

For an input size of 70,000 this algorithm takes ~4 seconds to run in C++. That difference is huge. Not to mention, I was able to use inputs that were about ~90,000 elements in size for C++, with it not even breaking past the 10 second mark.

Also, we can see that the curve is not as smooth as the Python graph. This could be due to some other processes running in the background (since I'm running on Windows 10) or some other reason.

Also, we can classify the time complexity of this algorithm as O(n^2), which just means that the time complexity for this algorithm is quadratic.

Let's move on to the last algorithm.

Performance of the 3rd Algorithm:

Algorithm Ex5(A, B):
    Input: Arrays "A" and "B" each storing n >= 1 integers.
    Output: The number of elements in B equal to the sum of
            prefix sums in A.
    c = 0
    for i = 0 to n - 1 do:
        s = 0
        for j = 0 to n - 1 do:
            s = s + A[0]
            for k = 1 to j do:
                s = s + A[k]
            if B[i] == s then:
                c = c + 1
    return c
    

Let's take a look at this code in Python:

def ex3(A, B):
    c = 0
    for i in range(len(A)):
        s = 0
        for j in range(len(A)):
            s = s + A[0]
            for k in range(1, j):
                s = s + A[k]
            if B[i] == s:
                c = c + 1
    return c

Now, let's analyze the timings:

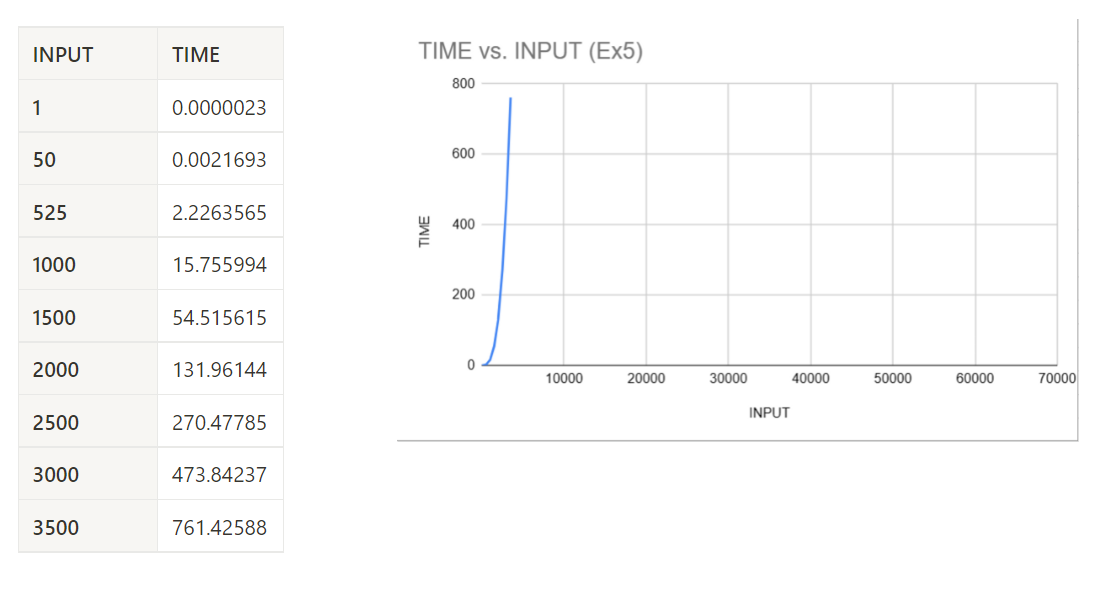
Woah, what's going on here? We can see that as our inputs starts to increase, the rate at which the algorithm runs also starts to increase, but it is increasing at a drastic rate.

In this case, we can see with an input size of 3500 that it takes 761 seconds for this algorithm to run in Python. You may be asking, "Did you actually sit through all 761 seconds?", the answer is yes. Yes, I did.

Now let's take a look at the C++ code:

double ex5(double A[], double B[], size_t n)
{
    double c = 0;
    for(size_t i = 0; i < n; i++)
    {
        double s = 0;
        for(size_t j = 0; j < n; i++)
        {
            s = s + A[0]
            for(size_t k = 1; k < j; k++)
            {
                s = s + A[k];
            }
            if(B[i] == s)
            {
                c = c + 1
            }
        }
    }
    return c;
}

Let's take a look at the graph.

Similar to the second algorithm, it is interesting to see that the curve is not as smooth as the Python graph.

Also, we can see that we can go well above an input size of 3500. My computer started acting up once I pushed the input size past 10,000 for C++. Not to mention, with an input size of 10,000 the algorithm averaged about 544-545 seconds.

We can classify this algorithm as having a time complexity of O(n!). Which just means that this algorithm is factorial, which runs very slowly.

Wrapping Up

I hope you found the differences of running times between Python and C++ just as fascinating as I have.

Also, just because Python runs slower than C++ for every algorithm does not mean that C++ is the "better" language. Both of these languages have their own purposes for the type of software you are trying to create.

C++ would be the preferred language if performance is critical. If you were programming games, operating systems, or communicating between machinery, C++ would be the better choice due to its compiled and fast nature.

Python would be preferred if you need to develop software quickly. Due to its easier learning curve, almost anyone can pick up Python and start creating software with it. Python also provides many resources for data science and machine learning.

Check out the code if you would like to try these tests on your own computer:

C++ Algorithm Anaylsis

C++ Algorithm Anaylsis. GitHub Gist: instantly share code, notes, and snippets.

262588213843476Gist

Python Algorithm Anaylsis

Python Algorithm Anaylsis. GitHub Gist: instantly share code, notes, and snippets.

262588213843476Gist

Cheers!