Recursion is a problem-solving technique in programming. In this article, you will learn how to use recursive functions in JavaScript.
What is a Recursive Function?
A recursive function is a function that calls itself somewhere within the body of the function. Below is a basic example of a recursive function.
function recursiveFunc() {
// some code here...
recursiveFunc()
}As you can see, the recursiveFunc function calls itself within the body of the function. It will repeat calling itself until the desired output is achieved.
So how do you tell the function when to stop calling itself? You do that using a base condition.
The Three Parts of a Recursive Function
Every time you write a recursive function, three elements must be present. They are:
- The function definition.
- The base condition.
- The recursive call.
When these three elements are missing, your recursive function won't work as you expect. Let's take a closer look at each one.
How to define a recursive function
You define a recursive function the same way you define regular JavaScript functions.
function recursiveFunc() {
// some code here...
} What differentiates recursive functions from regular JavaScript functions are the base condition and the recursive call.
What is a base condition?
When using a recursive function, the base condition is what lets the function know when to stop calling itself. Once the base condition is met, the recursion ends.
function recursiveFunc() {
if(base condition) {
// stops recursion if condition is met
}
// else recursion continues
recurse();
}Why do you need a base condition?
Without the base condition, you will run into infinite recursion. A situation where your function continues calling itself without stopping, like this:
function doSomething(action) {
console.log(`I am ${action}.`)
doSomething(action)
}
doSomething("running")Also, without a base condition, your function exceeds the maximum call stack. You will run into the error shown below.
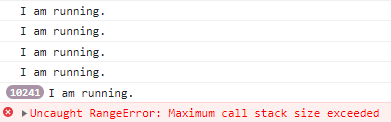
The Call Stack keeps track of what functions are currently running and the functions that are within them.
The call stack has a limit. And since a recursive function without a base condition will run infinitely, it exceeds the call stack's limit.
The base condition provides a way to break out when the function gets the desired output.
Example of recursive function
Let's see a simple example of a recursive function.
function doSomething(n) {
if(n === 0) {
console.log("TASK COMPLETED!")
return
}
console.log("I'm doing something.")
doSomething(n - 1)
}
doSomething(3)Here is the result when you pass the number 3 to the doSomething function.
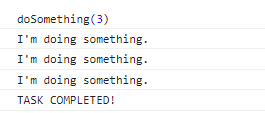
The base condition for the doSomething function is n === 0. Anytime the function is called, it first checks if the base condition is met.
If yes, it prints TASK COMPLETED!. If not, it continues with the rest of the code in the function. In this case, it will print I'm doing something. and then call the function again.
The recursive call
The recursive call is what handles the function calling itself again. In the doSomething function, the recursive call is the line below.
doSomething(n-1)Note what happens when the function calls itself. A new parameter n - 1 is passed to the function. On every iteration of a recursive call, the parameter will differ from that of the previous call.
The function will keep calling itself until the new parameter satisfies the base condition.
Recursion vs Loops
Recursion and loops work in similar ways. Every recursive function you write has an alternative solution with a loop.
For example, you can create a function to find the factorial of a given number using both recursion and loops.
How to find the factorial with a loop:
function findFactorial(num) {
let factorial = 1
for (let i = num; i > 0; i--) {
factorial *= i
}
return factorial
}
findFactorial(5) // 120To find the factorial using a loop, you first initialize a variable factorial with a value of 1.
Then you initiate the loop with the given number num. The loop will continue running until i > 0.
For each iteration, you multiply the current value of factorial by i. And you decrease the value of i by 1 until i is not greater than zero.
Finally, you return the value of the factorial when the loop finishes running.
How to find the factorial with recursion:
You can create the same solution with a recursive function.
function findFactorial(num) {
if (num === 0) return 1
let factorial = num * findFactorial(num - 1)
return factorial;
}
findFactorial(5) // 120First, you need a base condition num === 0.
You also need the recursive call findFactorial(num - 1) to ensure the number keeps reducing at each call when you pass a new parameter of n-1.
Then you multiply the result with the previous number num * findFactorial(num - 1) until the base condition is met.
So which is better – recursion or loops?
So which one is better? There's no right or wrong answer to that. It's up to you to decide. Depending on the problem you're solving, you may choose one over the other.
Optimize for the readability of your code. Sometimes, like in the factorial example, recursion leads to shorter and more readable code.
But recursive functions are not always intuitive. If that's the case, you should stick to loops.
Conclusion
In this article, you've learned what recursion is and how to create recursive functions in JavaScript.
Reading and writing recursive functions might be confusing at first. But remember, what makes recursive functions different from regular functions are the base condition and the recursive call.
Thanks for reading. And happy coding!

