What is a Search Algorithm?
This kind of algorithm looks at the problem of re-arranging an array of items in ascending order. The two most classical examples of that is the binary search and the merge sort algorithm.
Exponential Search
Exponential Search, also known as finger search, searches for an element in a sorted array by jumping 2^i elements in every iteration, where i represents the value of loop control variable, and then verifying if the search element is present between the last jump and the current jump.
Complexity Worst Case
O(log(N)) Often confused because of the name, the algorithm is named so not because of the time complexity. The name arises as a result of the algorithm jumping elements with steps equal to exponents of 2
Steps
- Jump the array
2^ielements at a time searching for the conditionArray[2^(i-1)] < valueWanted < Array[2^i]. If2^iis greater than the lenght of array, then set the upper bound to the length of the array. - Do a binary search between
Array[2^(i-1)]andArray[2^i]
Code
// C++ program to find an element x in a
// sorted array using Exponential search.
#include <bits/stdc++.h>
using namespace std;
int binarySearch(int arr[], int, int, int);
// Returns position of first ocurrence of
// x in array
int exponentialSearch(int arr[], int n, int x)
{
// If x is present at firt location itself
if (arr[0] == x)
return 0;
// Find range for binary search by
// repeated doubling
int i = 1;
while (i < n && arr[i] <= x)
i = i*2;
// Call binary search for the found range.
return binarySearch(arr, i/2, min(i, n), x);
}
// A recursive binary search function. It returns
// location of x in given array arr[l..r] is
// present, otherwise -1
int binarySearch(int arr[], int l, int r, int x)
{
if (r >= l)
{
int mid = l + (r - l)/2;
// If the element is present at the middle
// itself
if (arr[mid] == x)
return mid;
// If element is smaller than mid, then it
// can only be present n left subarray
if (arr[mid] > x)
return binarySearch(arr, l, mid-1, x);
// Else the element can only be present
// in right subarray
return binarySearch(arr, mid+1, r, x);
}
// We reach here when element is not present
// in array
return -1;
}
int main(void)
{
int arr[] = {2, 3, 4, 10, 40};
int n = sizeof(arr)/ sizeof(arr[0]);
int x = 10;
int result = exponentialSearch(arr, n, x);
(result == -1)? printf("Element is not present in array")
: printf("Element is present at index %d", result);
return 0;
}
Searching Linked Lists Versus Arrays
Suppose you have to search for an element in an unsorted linked list and array. In that case, you need to do a linear search (remember, unsorted). Doing a linear search for an element in either data structure will be an O(n) operation.
Now if you have a sorted linked list and array, you can still search in both the data structures in O(log n) time using Binary Search. Although, it will be a bit tedious to code while using linked lists.
Linked lists are usually preferred over arrays where insertion is a frequent operation. It's easier to insert in linked lists as only a pointer changes. But to insert in an array (the middle or beginning), you need to move all the elements after the one that you insert. Another place where you should use linked lists is where size is uncertain (you don't know the size when you are starting out), because arrays have fixed size.
Arrays do provide a few advantages over linked lists:
- Random access
- Less memory as compared to linked lists
- Arrays have better cache locality thus providing better performance
It completely depends on the use case for whether arrays or linked lists are better.
Linear Search
Suppose you are given a list or an array of items. You are searching for a particular item. How do you do that?
Find the number 13 in the given list.

You just look at the list and there it is!

Now, how do you tell a computer to find it.
A computer cannot look at more than the value at a given instant of time. So it takes one item from the array and checks if it is the same as what you are looking for.

The first item did not match. So move onto the next one.

And so on...
This is done till a match is found or until all the items have been checked.
In this algorithm, you can stop when the item is found and then there is no need to look further.
So how long would it take to do the linear search operation? In the best case, you could get lucky and the item you are looking at maybe at the first position in the array! But in the worst case, you would have to look at each and every item before you find the item at the last place or before you realize that the item is not in the array.
The complexity therefore of the linear search is O(n).
If the element to be searched presides on the the first memory block then the complexity would be O(1).
The code for a linear search function in JavaScript is shown below. This function returns the position of the item we are looking for in the array. If the item is not present in the array, the function would return null.
int linearSearch(int arr[], int num)
{
int len = (int)( sizeof(arr) / sizeof(arr[0]);
int *a = arr;
for(int i = 0; i < len; i++)
{
if(*(a+i) == num) return i;
}
return -1;
}
Example in JavaScript
function linearSearch(arr, item) {
// Go through all the elements of arr to look for item.
for (var i = 0; i < arr.length; i++) {
if (arr[i] === item) { // Found it!
return i;
}
}
// Item not found in the array.
return null;
}
Example in Ruby
def linear_search(target, array)
counter = 0
while counter < array.length
if array[counter] == target
return counter
else
counter += 1
end
end
return nil
end
Example in C++
int linear_search(int arr[],int n,int num)
{
for(int i=0;i<n;i++){
if(arr[i]==num)
return i;
}
// Item not found in the array
return -1;
}
Example in Python
def linear_search(array, num):
for index, element in enumerate(array):
if element == num:
return index
return -1
Example in Swift
func linearSearch(for number: Int, in array: [Int]) -> Int? {
for (index, value) in array.enumerated() {
if value == number { return index } // return the index of the number
}
return nil // the number was not found in the array
}
Example in Java
int linearSearch(int[] arr, int element)
{
for(int i=0;i<arr.length;i++)
{
if(arr[i] == element)
return i;
}
return -1;
}
Example in PHP
function linear_search($arr=[],$num=0)
{
$n = count($arr);
for( $i=0; $i<$n; $i++){
if($arr[$i] == $num)
return $i;
}
// Item not found in the array
return -1;
}
$arr = array(1,3,2,8,5,7,4,0);
print("Linear search result for 2: ");
echo linear_search($arr,2);
Global Linear Search
What if you are searching the multiple occurrences of an element? For example you want to see how many 5’s are in an array.
Target = 5
Array = [ 1, 2, 3, 4, 5, 6, 5, 7, 8, 9, 5]
This array has 3 occurances of 5s and we want to return the indexes (where they are in the array) of all of them. This is called global linear search. You will need to adjust your code to return an array of the index points at which it finds the target element. When you find an index element that matches your target, the index point (counter) will be added in the results array. If it doesn’t match the code will continue to move on to the next element in the array by adding 1 to the counter.
def global_linear_search(target, array)
counter = 0
results = []
while counter < array.length
if array[counter] == target
results << counter
counter += 1
else
counter += 1
end
end
if results.empty?
return nil
else
return results
end
end
Why linear search is not efficient
There is no doubt that linear search is simple but because it compares each element one by one, it is time consuming and hence not very efficient. If we have to find a number from say, 1000000 numbers and number is at the last location, linear search technique would become quite tedious. So, also learn about binary search, exponential search, etc. which are much more efficient than linear search.
Binary Search
A binary search locates an item in a sorted array by repeatedly dividing the search interval in half.
How do you search a name in a telephone directory?
One way would be to start from the first page and look at each name in the phonebook till we find what we are looking for. But that would be an extremely laborious and inefficient way to search.
Because we know that names in the phonebook are sorted alphabetically, we could probably work along the following steps:
- Open the middle page of the phonebook
- If it has the name we are looking for, we are done!
- Otherwise, throw away the half of the phonebook that does not contain the name
- Repeat until you find the name or there are no more pages left in the phonebook
[
]
Time complexity: As we dispose off one part of the search case during every step of binary search, and perform the search operation on the other half, this results in a worst case time complexity of O ( log2N ). The best case occurs when the element to be found is in the middle of the list. The best case time complexity is O ( 1 ).
Space complexity: Binary search takes constant or O ( 1 ) space meaning that we don't do any input size related variable defining.
for small sets linear search is better but in larger ones it is way more efficient to use binary search.
In detail, how many times can you divide N by 2 until you have 1? This is essentially saying, do a binary search (half the elements) until you found it. In a formula this would be this:
1 = N / 2^x
Multiply by 2x:
2^x = N
Now do the log2:
log2(2^x) = log2 N
x * log2(2) = log2 N
x * 1 = log2 N
This means you can divide log N times until you have everything divided. Which means you have to divide log N ("do the binary search step") until you found your element.
O ( log2N ) is such so because at every step half of the elements in the data set are gone which is justified by the base of the logarithmic function.
This is the binary search algorithm. It is elegant and efficient but for it to work correctly, the array must be sorted .
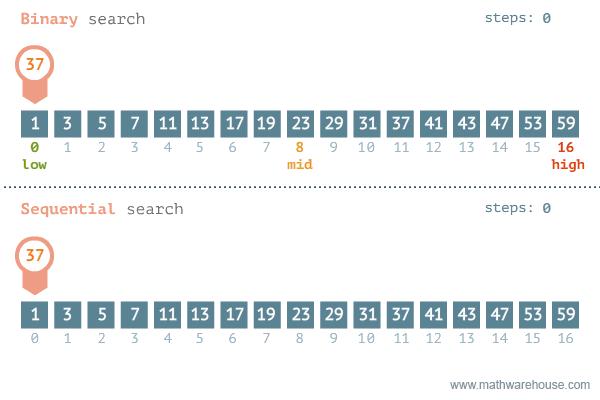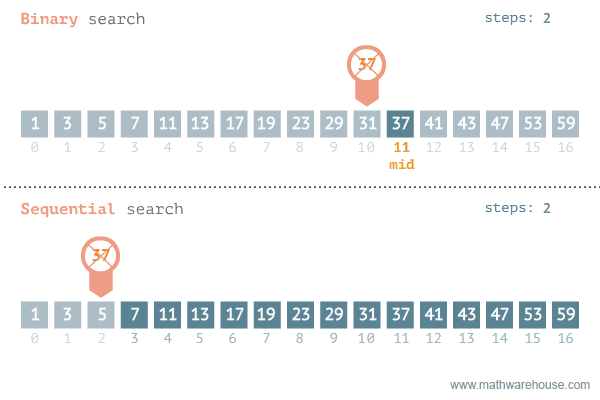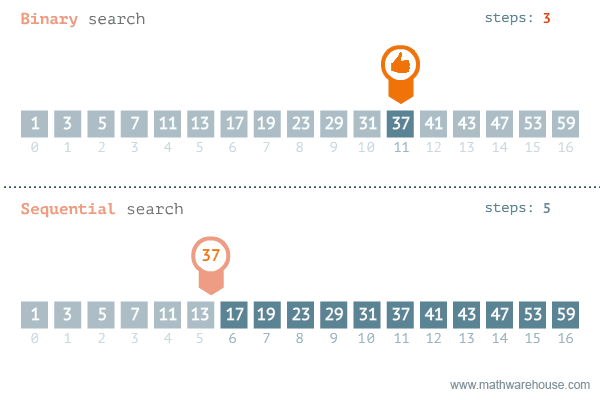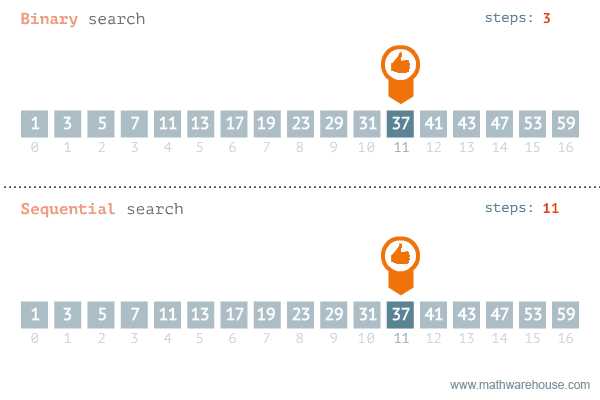
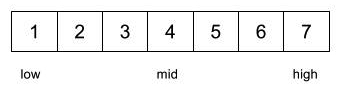
Find 5 in the given array of numbers using binary search.

Mark low, high and mid positions in the array.
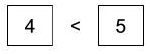
Compare the item you are looking for with the middle element.
Throw away the left half and look in the right half.
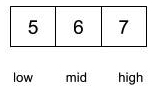
Again compare with the middle element.
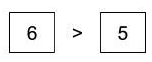
Now, move to the left half.

The middle element is the item we were looking for!
The binary search algorithm takes a divide-and-conquer approach where the array is continuously divided until the item is found or until there are no more elements left for checking. Hence, this algorithm can be defined recursively to generate an elegant solution.
The two base cases for recursion would be:
- No more elements left in the array
- Item is found
The Power of Binary Search in Data Systems (B+ trees): Binary Search Trees are very powerful because of their O(log n) search times, second to the hashmap data structure which uses a hashing key to search for data in O(1). It is important to understand how the log n run time comes from the height of a binary search tree. If each node splits into two nodes, (binary), then the depth of the tree is log n (base 2).. In order to improve this speed in Data System, we use B+ trees because they have a larger branching factor, and therefore more height. I hope this short article helps expand your mind about how binary search is used in practical systems.
The code for recursive binary search is shown below:
JavaScript implementation
function binarySearch(arr, item, low, high) {
if (low > high) { // No more elements in the array.
return null;
}
// Find the middle of the array.
var mid = Math.ceil((low + high) / 2);
if (arr[mid] === item) { // Found the item!
return mid;
}
if (item < arr[mid]) { // Item is in the half from low to mid-1.
return binarySearch(arr, item, low, mid-1);
}
else { // Item is in the half from mid+1 to high.
return binarySearch(arr, item, mid+1, high);
}
}
var numbers = [1,2,3,4,5,6,7];
print(binarySearch(numbers, 5, 0, numbers.length-1));
Here is another implementation in JavaScript:
function binary_search(a, v) {
function search(low, high) {
if (low === high) {
return a[low] === v;
} else {
var mid = math_floor((low + high) / 2);
return (v === a[mid])
||
(v < a[mid])
? search(low, mid - 1)
: search(mid + 1, high);
}
}
return search(0, array_length(a) - 1);
}
Ruby implementation
def binary_search(target, array)
sorted_array = array.sort
low = 0
high = (sorted_array.length) - 1
while high >= low
middle = (low + high) / 2
if target > sorted_array[middle]
low = middle + 1
elsif target < sorted_array[middle]
high = middle - 1
else
return middle
end
end
return nil
end
Example in C
int binarySearch(int a[], int l, int r, int x) {
if (r >= l){
int mid = (l + (r - l))/2;
if (a[mid] == x)
return mid;
if (arr[mid] > x)
return binarySearch(arr, l, mid-1, x);
return binarySearch(arr, mid+1, r, x);
}
return -1;
}
Python implementation
def binary_search(arr, l, r, target):
if r >= l:
mid = (l + (r - l))/2
if arr[mid] == target:
return mid
elif arr[mid] > target:
return binary_search(arr, l, mid-1, target)
else:
return binary_search(arr, mid+1, r, target)
else:
return -1
Example in C++
Recursive approach!
// Recursive approach in C++
int binarySearch(int arr[], int start, int end, int x)
{
if (end >= start)
{
int mid = (start + (end - start))/2;
if (arr[mid] == x)
return mid;
if (arr[mid] > x)
return binarySearch(arr, start, mid-1, x);
return binarySearch(arr, mid+1, end, x);
}
return -1;
}
Iterative approach!
int binarySearch(int arr[], int start, int end, int x)
{
while (start <= end)
{
int mid = (start + (end - start))/2;
if (arr[mid] == x)
return mid;
if (arr[mid] < x)
start = mid + 1;
else
end = mid - 1;
}
return -1;
}
Example in Swift
func binarySearch(for number: Int, in numbers: [Int]) -> Int? {
var lowerBound = 0
var upperBound = numbers.count
while lowerBound < upperBound {
let index = lowerBound + (upperBound - lowerBound) / 2
if numbers[index] == number {
return index // we found the given number at this index
} else if numbers[index] < number {
lowerBound = index + 1
} else {
upperBound = index
}
}
return nil // the given number was not found
}
Example in Java
// Iterative Approach in Java
int binarySearch(int[] arr, int start, int end, int element)
{
while(start <= end)
{
int mid = start + ( end - start ) / 2;
if(arr[mid] == element)
return mid;
if(arr[mid] < element)
start = mid+1;
else
end = mid-1;
}
return -1;
}
// Recursive Approach in Java
int binarySearch(int[] arr, int start,int end , int element)
{
if (end >= start)
{
int mid = start + ( end - start ) / 2;
if(arr[mid] == element)
return mid;
if(arr[mid] < element)
return binarySearch( arr , mid + 1 , end , element );
else
return binarySearch( arr, start, mid - 1 , element);
}
return -1;
}
