by Ben Mmari
The Computer Science of Evolution: an Introduction to Genetic Algorithms
Being a computer scientist with an interest in evolution and biological processes, the topic of genetic algorithms, and more broadly, evolutionary computation is to me what a candy shop is to a 5-year-old: Heaven. The mere possibility of being able to merge two of my interests in such a seamless manner has been extremely exhilarating, and it would be wrong for me to keep this knowledge and excitement all to myself.
So in an attempt to test out some of my learnings thus far, and share my findings with the rest of the world, I have decided to put together a series of articles on this topic.
In this post, I will provide a brief introduction to genetic algorithms and explain how they imitate the same natural processes that have been taking place on Earth for billions of years.
Life on Earth
Over the past 3.5 billion years, mother nature, father time, evolution and natural selection have collaborated together to produce all of the specialized forms of life that we see on earth today: like the carnivorous Venus Flytrap plant; the ocean-dwelling Atlantic Flying Fish; echolocation-using bats; long-necked giraffes; super-quick cheetahs, dancing Honeybees; and of course, yours truly, the street smart Homo sapiens.

Needless to say, life on Earth is one of, if not the most successful experiments ever run in our universe; and judging from the impressive outcomes of this experiment, it is clear that evolution is clearly onto something.
Recently, we humans — just one of the many end products of this process — realized that we could also take advantage of this ingenious approach to progressive problem solving, and since the 1950s, computer scientist, geneticists, mathematicians, and biologist, have attempted to mimic these biological processes through the implementation of computer simulations. With the aim of producing optimal solutions for difficult, non-trivial problems, in an efficient manner.

The blind watchmaker
One of the first books I came across that sparked my interest in the field of evolutionary biology was The Blind Watchmaker, by Richard Dawkins. In this book, Richard Dawkins explains how complex mechanisms like echolocation (a process that bats use to navigate, hunt and forage, also known as bio-sonar), complex structures like spiderwebs (which spiders use to attract and catch their prey), and complex instruments like the human eye (those two spherical objects that you are currently using to read this article) are simply the result of thousands, if not millions of years of evolution and adaptation.
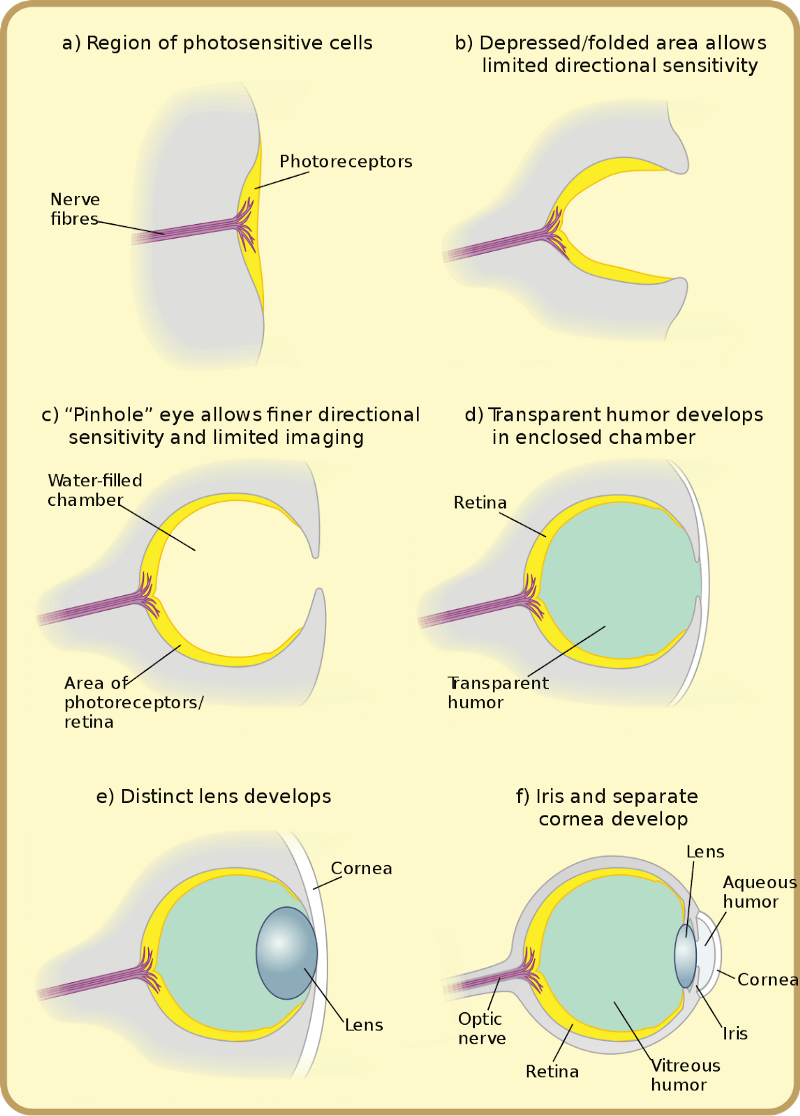
Even though these marvels of nature give the impression that they were built with a purpose from the get-go (i.e by a conscious ‘maker’), they are actually just a result of iterations upon iterations of trial and error, bundled up with ever-changing selection pressure (i.e a change in climate, habitat, or the behaviour and capabilities of predators or prey). So while they may look and behave like the outcome of precise, forward-thinking engineering, they are actually the result of a completely blind process, a process that does not know beforehand what the perfect ‘solution’ would be.
What are genetic algorithms and why do we need them?
Genetic algorithms are a technique used to generate high-quality solutions to optimization and search problems, which are based on fundamental biological processes. These algorithms are used in situations where the possible range of solutions is very large, and where the more basic approaches to problem-solving like exhaustive search/brute force would consume too much time and effort.
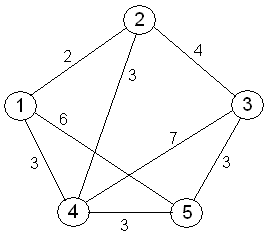
The traveling salesman problem asks the following question: “Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?” It is an NP-hard problem in combinatorial optimization.
We can use genetic algorithms to provide high-quality solutions to this problem, at a much lower cost than the more primitive problem-solving techniques, like exhaustive search, which would require you to permute through all possible solutions.
How do genetic algorithms work?
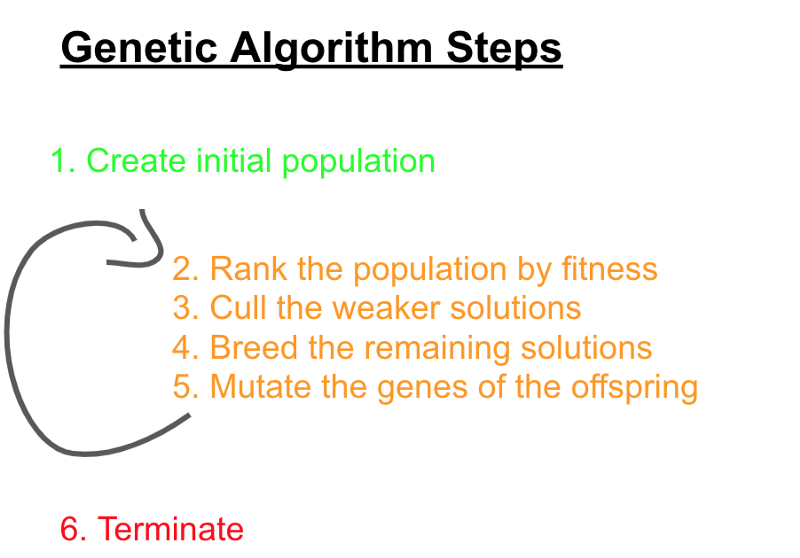
An algorithm works by iterating through a number of steps, up until it reaches a predefined termination point. Each iteration of the genetic algorithm produces a new generation of possible solutions, which, in theory, should be an improvement on the previous generation.
The steps are as follows:
1. Create an initial population of N possible solutions (the primordial soup)
The first step of the algorithm is to create an initial group of solutions that serve as the base solutions in generation 0. Each solution in this initial population will carry a set of chromosomes, which are made up of a collection of genes, where each gene is assigned to one of the possible variables of the problem. It is important that the solutions in the initial population are created with randomly assigned genes, in order to have a high degree of genetic variation.
2. Rank the solutions of the population by fitness (survival of the fittest, part 1).
In this step, the algorithm needs to be able to determine what makes one solution more ‘fit’ than another solution. This is determined by the fitness function. The aim of the fitness function is to evaluate the genetic viability of the solutions within the population, placing those with the most viable, favorable & superior genetic traits at the top of the list.
In the traveling salesman problem, the fitness function could be a calculation of the total distance traveled by the solution. Where a shorter distance equates to higher fitness.
3. Cull the weaker solutions (survival of the fittest, part 2)
In this step, the algorithm removes the less fit solutions from the population. The ‘fittest’ does not necessarily mean the strongest, the fastest or the fiercest, as humans usually tend to assume. Survival of the fittest simply means that the better equipped an organism is to survive in its environment, the more likely it is to live long enough to reproduce and spread its genes onto the next generation.
Steps 3 and 4 are collectively known as selection.
4. Breed the stronger solutions (survival of the fittest, part 3)
The remaining solutions are then paired with each other in order to mate and reproduce offspring. During this process, in its most basic form, each parent will contribute a % of their genes (in nature it is a 50/50 split) to each of their offspring, where P1(G)% +P2(G)% = 100%. The process of determining which of the parents’ genes will be inherited by the offspring is known as crossover.
5. Mutate the genes of the offspring (mutation)
The offspring will contain a percentage of the ‘mother’s’ genes, and a percentage of the ‘fathers’ genes and occasionally there will be a ‘mutation’ of one or more of these genes. A mutation is essentially a genetic abnormality, a copying error which causes one or more of the offspring’s genes to differ from the genes it inherited from its parents. In genetic algorithms, in some cases a mutation will increase the fitness of the offspring, in other cases, it will reduce it.
It is important to note that there does not need to be a mutation with each offspring, the required mutation frequency can also be a parameter of the algorithm.
In genetic algorithms, selection, crossover, and mutation are known as genetic operators.
6. Termination
Steps 2 to 5 will be repeated up until a predefined termination point. This termination point can be one of the following:
- Maximum time/resource allocation reached.
- Fixed number of generations have passed.
- The fitness of the dominant solution cannot be surpassed by any future generations.
Solution convergence
1. Global optimum
In the ideal situation, the fittest solution will have the highest fitness value possible, i.e it will be the optimal solution, meaning that there will be no need to continue with the algorithm and produce further generations.
2. Local optimum
In some cases, if the parameters of the algorithm are not reasonable, the population may tend towards a premature convergence upon a less optimal solution, which is not the global optimum that we are after, but rather a local one. Once here, continuing the algorithm and producing further generations may be futile.

What would happen if there were no mutations?
On first glance, mutations may seem like an unnecessary, irrelevant part of the process. But without this fundamental aspect of randomness, evolution by natural selection would be completely restricted to the genetic variety set by the initial population, and there would be no new traits introduced into the population after that. This would severely hinder nature’s problem-solving capabilities, and life on earth would not be able to ‘adapt’ to its environment, at least not physically.
If this was the case in our genetic algorithm, at some point in our simulation, the future generations of the population would not be able to explore part of the solution space that their predecessors did not explore. A simulation without any mutations would severely restrict the genetic variation within the population, and in most cases — depending on the initial population — prevent us from ever reaching a global optimum.

What would happen if the population size was not large enough?
I was recently at the Jukani Wildlife Sanctuary in Plettenberg, where I had the privilege of meeting a white tiger. He was a truly majestic animal. He was large, he looked ferocious, and, he was also 80% blind and getting progressively worse as the years went by.
Why was he blind? Because he is a product of generations of inbreeding. These white tigers are only produced when two tigers that carry a recessive gene controlling coat color are bred together. Thus, in order to ensure the continuation of these tigers in captivity, people have been breeding these tigers within a very limited population in order to either show them off at circuses, parade them at zoos, or keep them as household pets.
But one of the negative effects of inbreeding is that you severely limit the genetic variation within the species, which progressively increases the chances that harmful recessive traits will be passed onto the offspring.

Even in the wild, inbreeding can still be a massive problem. Over the past few decades, the rhino population in Southern Africa has been significantly impacted due to poaching, and if the population size reaches a low enough number it would mean that maintaining the genetic diversity of these threatened rhino species would be extremely difficult. So even if poaching doesn’t completely lead them to extinction, inbreeding could.

Of course, humans are no strangers to inbreeding. One famous result of continuous inbreeding within our own species is Charles (Carlos) the II of Spain.
“The Habsburg King Carlos II of Spain was sadly degenerated with an enormous misshapen head. His Habsburg jaw stood so much out that his two rows of teeth could not meet; he was unable to chew. His tongue was so large that he was barely able to speak. His intellect was similarly disabled.”

‘Inbreeding’ in our genetic algorithm, essentially means the breeding of solutions that have a very similar genetic makeup, which, thankfully, in this case, would not result in offspring with a predisposition to any physical abnormalities. But if the population is very small and if all of the solutions share a very similar genetic makeup then the fitness of the future generations of the population will be severely restricted. Meaning that it could take much longer to converge upon a globally optimal solution if we even get there at all.
Inbreeding is not always a bad thing, it just depends on which stage of the simulation you are in. In very advanced stages of the simulation, as the population converges towards a global/local optima, it is obviously very hard to avoid inbreeding, because, in some cases, many of the dominant solutions will be very similar to each other, and thus, will share a lot of the same genetic traits.
Wrapping up
Alright, that should cover the basics. If you have any questions, requests, or genetic mutations to contribute, please leave a comment below.
In the next post, we will delve into some code as we look at how each of the genetic operators outlined above plays out in the world of programming. I used the Ruby programming language for the software simulation that I worked on, and in it, I show how in only a few generations, a genetic algorithm can produce a predefined word or phrase from an initial collection of complete and utter gibberish. All of the code will be hosted on Github.