Understanding Randomness
When you hear the word "randomness," what usually comes to mind? You may think of something intangible, an abstract concept without a specific shape or form – it's random.
But randomness is much more than an abstract idea – it's a fundamental aspect of our daily decisions and choices. Whether it's deciding what to eat for breakfast or picking a number from 1 to 10 in a game, randomness plays a crucial role.
Randomness isn't just about unpredictability. It's also about the lack of pattern or predictability in events. For instance, when you toss a coin, the outcome of heads or tails is random because it's equally likely and unpredictable.
Why is Randomness Important in Software Engineering?
This concept is incredibly important in the field of software engineering, where generating true randomness can enhance security, simulations, and algorithms. In software development, this unpredictability is not just a feature—it's a fundamental requirement for various critical functions.
Security
The most crucial role of randomness in software is in the realm of security. Random numbers are used to generate secure keys for encryption, ensuring that sensitive data—be it personal information, financial details, or confidential communications—is protected from unauthorized access.
The randomness ensures that these keys cannot be easily predicted or replicated, fortifying the security barriers (see more in the Randomness in Cryptographic Systems section)
Testing and Quality Assurance
Developers use random inputs to simulate how software might perform under different conditions. This approach helps uncover unexpected bugs and ensures that the software can handle a variety of scenarios, improving its reliability and stability.
Companies like Netflix, Facebook, Google use Chaos Engineering to make their systems more reliable (learn more in the Chaos Engineering section).
Simulation and Modeling
Randomness is a key component in simulations that mimic real-world phenomena, which can be inherently unpredictable. Whether it's modeling climate patterns, economic markets, or traffic flows, randomness helps create more accurate models that better reflect the complexity of these systems.
Additional Applications
Randomness is used in many areas and it helps distribute tasks across servers in load balancing, improves efficiency in traffic routing, and adds realism in image generation. Also, its crucial for creating unique identifiers like GUIDs (Globally Unique Identifiers) and shuffling playlists to enhance user experience. As you can see, the use cases for randomness are numerous.
Prerequisites
This article is designed to be accessible, with explanations straightforward enough for readers with various backgrounds. However, a few basic prerequisites can enhance your understanding:
- Basic Programming Knowledge: While not essential, some familiarity with programming concepts in languages like C#, Java, or Python could help you grasp examples of how randomness is implemented in code more quickly.
- Elementary Math Skills: A basic understanding of probability and statistics is beneficial but not necessary, as the article aims to explain these concepts in simple terms.
- Introductory Cryptography: If you're curious about the security aspects of randomness, some background in cryptography concepts like encryption and key generation could be helpful.
Overall, the article is structured to be easy to follow, with no advanced knowledge required. It's meant to introduce the concept of randomness in software engineering broadly, making it suitable for readers from diverse fields.
Here's what we'll cover in this article:
- Understanding Randomness
- Coin Toss Paradigm
- The Illusion of Human Randomness
- How Random Number Generators Work
- True Random Number Generation (TRNG) and Entropy Sources
- Randomness in software testing
- Randomness in Cryptographic Systems
- Randomness in Simulation and Modeling
- Future of Randomness in Software Engineering
- Wrapping Up
Coin Toss Paradigm

Is tossing a coin truly a random event? At first glance, a coin toss represents the paradigm of randomness : two outcomes, each with an equal chance of occurring.
But if we dive deeper into the physics behind a coin toss, the story starts to unfold differently. Hypothetically, if we could control and replicate every variable involved in the toss – the force applied, the angle of the toss, the air resistance, and even the surface it lands on – would the outcome still be unpredictable?
The answer leans towards a surprising declaration: in a perfectly controlled environment, the result of a coin toss could be predicted with near certainty. This challenges our understanding of randomness, suggesting that what we often perceive as random is influenced by numerous factors, many of which are beyond our control or too complex to replicate in practice.
Thus, we arrive at an insightful conclusion that randomness ≈ the result of variables that are exceedingly difficult to replicate.
Big research from the University of California at Berkeley, titled “Dynamical Bias in the Coin Toss”, delves into this phenomenon:
Abstract: We analyze the natural process of flipping a coin which is caught in the hand. We show that vigorously flipped coins tend to come up the same way they started. The limiting chance of coming up this way depends on a single parameter, the angle between the normal to the coin and the angular momentum vector. Measurements of this parameter based on high-speed photography are reported. For natural flips, the chance of coming up as started is about .51

The Illusion of Human Randomness
For humans, it's an easy task to generate a random number, say a random word, or make a random decision. But again, is it really a random thing and can it be somehow predicted like we have stated for a coin toss?
If you have seen the 2015 movie Focus, you may remember the "priming" scene where they spend the day "priming" their victim to subconsciously recognize and choose the number 55 by having it represented all around him.
Priming is one of the most important psychological principles to understand because it influences behavior through implicit memory. In other words, exposure to a cue in one setting can form an association that carries into another.
One of the examples of priming comes to us from a supermarket bottle shop. Imagine one week you go into the bottle shop and there’s some French music playing in the background. You buy your wine and leave.
Now imagine you return a week later, but this time German music is piping through the speakers. Again, you buy your wine and leave. Chances are that when French music was playing, you purchased French wine, and when German music was playing, German wine – just like 77% and 73% of research participants did.
Were these consumers aware of the music and its impact on their decision? 86% of people said no, the music had no effect.
This phenomenon underscores a profound truth: whether knowingly or not, we are both the primers and the primed. Our perceived randomness in decision-making is continuously shaped by the stimuli around us. This reveals that the essence of human randomness is far more complex and influenced than we might initially believe.
How Random Number Generators Work
Let’s take a journey back to the early days of computing to understand the evolution of random number generators.
Initially, computers were quite basic compared to today’s sophisticated machines. Essentially, a computer operates on a strict set of instructions : it cannot spontaneously generate a number as humans might randomly choose a number from 1 to 10.
For a computer, generating a random number requires specific instructions. Today, this task has become straightforward in many programming languages through built-in functions. For example, in C#, you can generate a random number between 1 and 10 with this simple command:
Random.Next(1, 10) // <-- Generates a radom number from 1 to 10The interesting part begins when we look under the hood.
Simple random number generator
What if you were given a task to create a function that generates a random number? Let’s say you have this function:
public static int GenerateRandomNumber(int start, int end)
{
return ✨🪄 magic ✨🪄
}One of the simplest ways to do this is using a Linear Congruential Generator (LCG). The example below is a simplistic approach and you shouldn't use it for cryptographic purposes or applications requiring high levels of randomness.
using System;
class SimpleRandomGenerator
{
private long seed;
private const long a = 25214903917;
private const long c = 11;
private long m = (long)Math.Pow(2, 48);
public SimpleRandomGenerator(long seed)
{
this.seed = seed;
}
public int Next(int min, int max)
{
// Update the seed
seed = (a * seed + c) % m;
// Ensure the result is within the bounds [min, max)
int result = (int)(min + (seed % (max - min)));
return result;
}
}
class Program
{
static void Main(string[] args)
{
var generator = new SimpleRandomGenerator(DateTime.Now.Ticks);
for(int i = 0; i < 15; i++)
{
var rndNumber = generator.Next(1, 101);
Console.WriteLine($"Random number between 1 and 100: {rndNumber}");
}
}
}
/* Output
Random number between 1 and 100: 78
Random number between 1 and 100: 9
Random number between 1 and 100: -48
Random number between 1 and 100: 71
Random number between 1 and 100: 6
Random number between 1 and 100: 45
Random number between 1 and 100: 64
Random number between 1 and 100: 99
Random number between 1 and 100: -34
Random number between 1 and 100: 85
Random number between 1 and 100: -44
Random number between 1 and 100: -25
Random number between 1 and 100: 26
Random number between 1 and 100: -27
Random number between 1 and 100: 24
*/This example uses the Linear Congruential Generator (LCG) method, which is a basic pseudorandom number generator.
LCGs are one of the oldest and simplest methods for generating sequences of pseudo-random numbers, and they operate based on a simple mathematical formula: "new seed = (a×seed+c) mod m" . The seed is typically initialized using a value with sufficient entropy, such as the current time (DateTime.Now.Ticks in this case). The Next method generates a new "random" number within the specified range [min, max).
Here's the step-by-step logic:
- Update the Seed: The seed is updated using the LCG formula mentioned above. This step is critical, as it uses the old seed to produce a new one, ensuring that each call to
Nextresults in a different output. - Scaling the Output: Once the new seed is calculated, it needs to be adjusted to fall within the user-specified range
[min, max).
– The modulus operationseed % (max - min)scales the seed to a value within the range of 0 to(max - min) - 1.
– Addingminshifts this scaled value into the desired range, ensuring that the result is at leastminbut less thanmax.
True Random Number Generation (TRNG) and Entropy Sources
Random number generation based on natural events or hardware characteristics involves using unpredictable, non-deterministic sources to generate randomness. This approach is often referred to as using "entropy sources" or "true random number generation" (TRNG).
Unlike pseudo-random number generators (PRNGs) that use mathematical algorithms and require a seed value, true random number generators derive their randomness from physical events that are almost unpredictable. Here are a few examples:
Earthquakes in TRNG
Earthquakes generate seismic data that is almost unpredictable and can be used as a source of randomness. By measuring seismic activity through geophones or seismographs, the minute variations in the Earth's movement can be converted into random numbers.
Earthquakes occur due to the sudden release of energy in the Earth's crust, resulting in the ground shaking. This energy release is unpredictable and varies in magnitude, location, and frequency. The unpredictability of the timing, duration, and intensity of seismic events makes this a viable entropy source.
Additional technical details
Here are some additional technical details about earthquakes in TRNG:
Data collection is typically done using instruments called seismometers or geophones, which are sensitive to ground vibrations. These devices convert the kinetic energy of ground movements into electrical signals that can then be digitized and analyzed.
This process might include:
- Signal Conditioning and Filtering: Filtering the seismic signals to isolate the random components from predictable noise or background vibrations.
- Digitization: Converting the analog signals into digital values, which typically involves sampling the signal at regular intervals and quantizing these samples into digital values.
The raw digital data derived from seismic activity might not be uniformly random due to natural biases in how earthquakes occur or how data is collected.
To ensure that the numbers generated are suitable for use in applications requiring high-quality randomness (such as cryptographic systems), further processing might be necessary.
Here are the common techniques:
- Debiasing: Applying algorithms to remove any predictable patterns or biases from the data.
- Whitening: Transforming the data to ensure a uniform distribution across all possible values. This often involves statistical tests to adjust the output until it meets the criteria for randomness.
Using earthquakes for random number generation could be particularly valuable in applications where an external, unpredictable source of randomness is beneficial.
But there are cons and practical considerations:
- Geographical Limitations: Not all locations experience frequent seismic activity, which could limit the availability of this method to specific regions.
- Event Rarity: Significant seismic events are relatively rare and unpredictable in timing, which might not provide a steady or reliable source of randomness when needed.
- Data Collection and Processing Overhead: The infrastructure and computational effort required to capture, process, and utilize seismic data for random number generation can be significant.
Hardware Events in TRNG
Hardware-based random number generators (HRNGs) use physical processes within computing devices to generate randomness. Examples include:
Thermal Noise (Johnson-Nyquist Noise):
Thermal noise, also known as Johnson-Nyquist noise, is a type of interference naturally present in all electronic devices and circuits. It’s caused by the random motion of electrons within a material due to heat. This phenomenon can be used as a source of randomness for generating random numbers in hardware devices.
Every material that conducts electricity has electrons, which are tiny particles that move around and carry electrical current. Even when a device isn’t actively being used, these electrons are never completely still – they move randomly because of the heat energy within the material. The higher the temperature, the more active the electrons become.
Thermal noise is generated by the inherent energy present in all materials at temperatures above absolute zero (-273.15°C or -459.67°F). At these temperatures, electrons gain energy and start moving randomly. This movement causes tiny, random fluctuations in the electrical current when measured across components like resistors.
Thermal noise is ideal for cryptographic applications where high security is essential. This includes key generation and secure communications where unpredictability is paramount to preventing attacks.
In developing secure communication protocols for applications like instant messaging, VoIP, or data transmission systems, thermal noise can be used to generate encryption keys that are nearly impossible to predict, enhancing security.
Clock Drift
Clock drift occurs due to the slight and unpredictable variations in the timing mechanisms (like crystal oscillators) of computers and other digital devices. Clock drift exploits the natural variability in hardware clocks, which are designed to measure time but can drift apart due to minor differences in the frequency of their oscillators.
By comparing the time reported by two or more independent clocks, small differences that occur naturally and unpredictably can be measured. These differences are influenced by factors such as temperature changes, hardware imperfections, and supply voltage variations.

Photonic Emission
Photonic emission-based random number generation uses the process of light emission to create random numbers. This approach relies on the quantum nature of light – specifically, the behavior of photons, which are tiny particles that make up the light.
Photonic emission occurs when energy is released from atoms in the form of light. This happens in devices like LEDs (light-emitting diodes) and lasers.
In an LED, when electricity flows through the device, it excites electrons (tiny negatively charged particles) to higher energy states. As these electrons return to their normal states, they release energy in the form of photons.
The exact moment a photon is emitted is inherently unpredictable due to the principles of quantum mechanics, where particles like electrons behave in a probabilistic manner.
To turn photonic emission into random numbers, we first need to detect these photons. We can do this using a device called a photodetector, which captures the light and converts each photon hit into an electrical signal.
The key to randomness lies in the timing of each photon’s arrival at the detector. Since the emission of each photon is random, the times they are detected are also random. These times are then recorded with high precision.
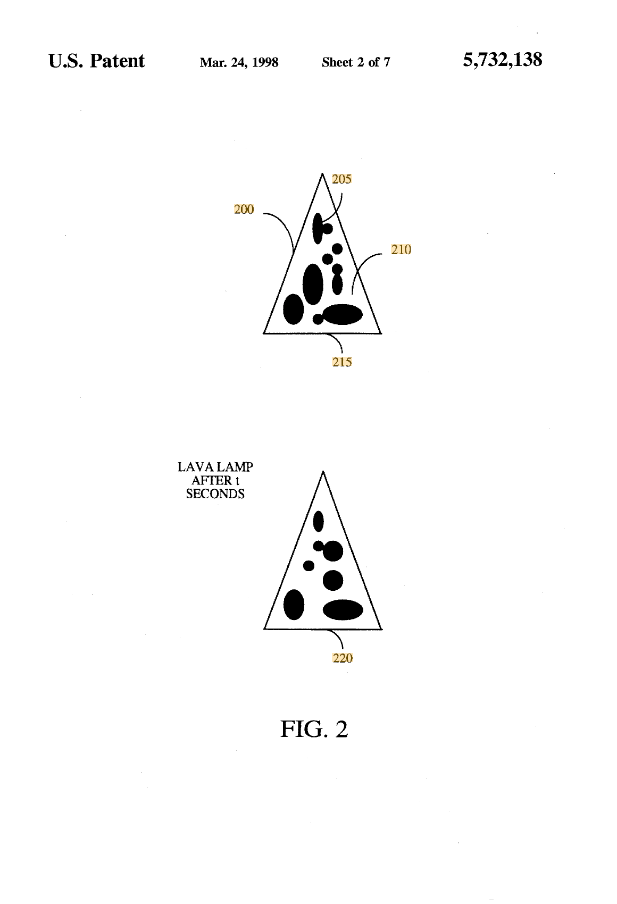
Cloudflare’s Lava Lamps for Randomness
Cloudflare, a web performance and security company, has set up a wall of lava lamps in the lobby of their San Francisco office. The setup is known as the “LavaRand” system. It leverages the unpredictable and ever-changing movements of the “lava” inside these lamps to generate randomness.

How LavaRand Works:
The process starts with visual capturing. A camera is pointed at the wall of lava lamps. The lamps contain blobs of wax in a liquid that expand and move in unpredictable ways when heated.
As the wax heats up, it rises, and as it cools, it falls, creating an ever-changing, visually chaotic display.
The camera takes images of the lava lamps at regular intervals. Each image captures a unique, random pattern of swirling wax. These images are then processed using computer algorithms to extract random data from the patterns observed in the images.
Relation to Photonic Emission:
While Cloudflare’s Lava Lamps use a form of photonic emission, it’s indirect. The photonic emission in this context is the light emitted by the lamps, which illuminates the wax inside.
The random number generation process, however, primarily relies on the chaotic physical movements of the wax, which are captured by the light and recorded by a camera. The randomness comes from how the light and shadows play off the moving lava, rather than the emission and detection of photons at a quantum level (which is more typical in photonic emission RNG systems using LEDs or lasers).
Information from Cloudflare's official website:
LavaRand is a system that uses lava lamps as a secondary source of randomness for our production servers. A wall of lava lamps in the lobby of our San Francisco office provides an unpredictable input to a camera aimed at the wall. A video feed from the camera is fed into a CSPRNG, and that CSPRNG provides a stream of random values that can be used as an extra source of randomness by our production servers. Since the flow of the “lava” in a lava lamp is very unpredictable,1 “measuring” the lamps by taking footage of them is a good way to obtain unpredictable randomness. Computers store images as very large numbers, so we can use them as the input to a CSPRNG just like any other number.
We’re not the first ones to do this. Our LavaRand system was inspired by a similar system first proposed and built by Silicon Graphics and patented in 1996 (the patent has since expired).
Hopefully, we’ll never need it. Hopefully, the primary sources of randomness used by our production servers will remain secure, and LavaRand will serve little purpose beyond adding some flair to our office. But if it turns out that we’re wrong, and that our randomness sources in production are actually flawed, then LavaRand will be our hedge, making it just a little bit harder to hack Cloudflare.
Read more here.
Human Factors in TRNG
Mouseware
Some tools like Mouseware use human factors to generate randomness. Mouseware uses a cryptographically secure random number generator based on your mouse movements to generate secure, memorable passwords. Passwords are generated entirely in the browser, and no data is ever sent over the network.
For those generated passwords, it would take 22400.7 years to guess at 1000 guesses/second and 2.0 hours to guess at 100 billion guesses/second.
- 1000 guesses/second is a worst-case web-based attack. Typically this is the only type of attack feasible against a secure website.
- 100 billion guesses/second is a worst-case offline attack when a hashed password database is stolen by someone with nontrivial technical and financial resources.
You can read more about Mouseware on their website.
Randomness in Software Testing
Chaos Monkey developed my Netflix

Chaos Monkey is an innovative tool developed by Netflix. It's responsible for randomly terminating Netflix's instances in production to ensure that engineers implement their services to be resilient to instance failures.
Imagine a virtual, mischievous monkey randomly tinkering with the network—shutting down instances, disconnecting servers, or overloading systems to simulate possible failures.
Although it might seem counterintuitive, the purpose of Chaos Monkey is to proactively provoke controlled failures. This strategy allows Netflix's engineers to test how well their systems can handle unexpected disruptions. The aim is to identify and resolve weaknesses before they impact users, ensuring that the infrastructure is robust enough to withstand real-world issues.
For instance, if Chaos Monkey randomly terminates a server and everything continues to run smoothly, that’s a win. If problems arise, engineers quickly analyze and rectify them, thereby strengthening the system. This continuous testing and improvement cycle helps ensure that when you settle in to binge-watch your favorite series, you experience uninterrupted streaming.
Thanks to tools like Chaos Monkey and the principles of Chaos Engineering, Netflix can deliver a seamless viewing experience. Next time you watch a show without any glitches, remember the behind-the-scenes efforts of these unsung heroes keeping your entertainment flawless.
This tool is also available for open source usage. Check out the docs here.
Randomness in Cryptographic Systems
Randomness plays a critical role in cryptographic systems, forming the backbone of security protocols across the digital landscape. This section explores why randomness is essential in cryptography, how it is generated, and the challenges involved in ensuring its effectiveness.
In cryptographic systems, randomness is used to generate keys, initialize cryptographic algorithms, and for non-repudiation processes like digital signatures and secure communications.
The strength and security of almost all cryptographic techniques depend on the quality of the randomness used. If the randomness is predictable, so too are the cryptographic keys, making the system vulnerable to attacks.
If we encrypt the text “Hello World”, we will get this text “oO64D2IzNWKSQnDM8fcZ/w==”. To see the power of encryption, let’s also encrypt variations of the text: “HelloWorld” (without a space) and “Hello world” (with lowercase), while also experimenting with a different encryption key.
Here are the outcomes:
╔═════════════╦═══════════╦══════════════════════════╗
║ Text ║ Password ║ Encoded value ║
╠═════════════╬═══════════╬══════════════════════════╣
║ Hello World ║ 1234 ║ oO64D2IzNWKSQnDM8fcZ/w== ║
╠─────────────╬───────────╬──────────────────────────╣
║ HelloWorld ║ 1234 ║ KvqAEHQhP9iBdFWhOUcYVg== ║
╠─────────────╬───────────╬──────────────────────────╣
║ Hello world ║ 1234 ║ jdKRaAw9ULCFb627e3mNpQ== ║
╠─────────────╬───────────╬──────────────────────────╣
║ Hello World ║ 123 ║ S/eGTyDQsgLwcEIrCWUAJw== ║
╠─────────────╬───────────╬──────────────────────────╣
║ HelloWorld ║ 123 ║ /JRa5+mllydL/F0m7NuxYA== ║
╠─────────────╬───────────╬──────────────────────────╣
║ Hello world ║ 123 ║ s3AydwlvlgHCcpiAhaurXg== ║
╚═════════════╩═══════════╩══════════════════════════╝If you consider the above table, you’ll notice that even a small change, such as a change in spacing or a single character, leads to a complete transformation of the encrypted text.
This means that if the intruder manages to obtain both the original text and its encrypted form, they would still face a significant challenge in trying to guess the password required to unlock the entire database.
Could you hack the encryption?
Brute force attacks are a straightforward yet powerful method used by attackers to crack passwords and encryption keys.
A brute force attack involves systematically checking all possible combinations until the correct one is found. Attackers use brute force methods to try every possible key or password until they decrypt the targeted data.
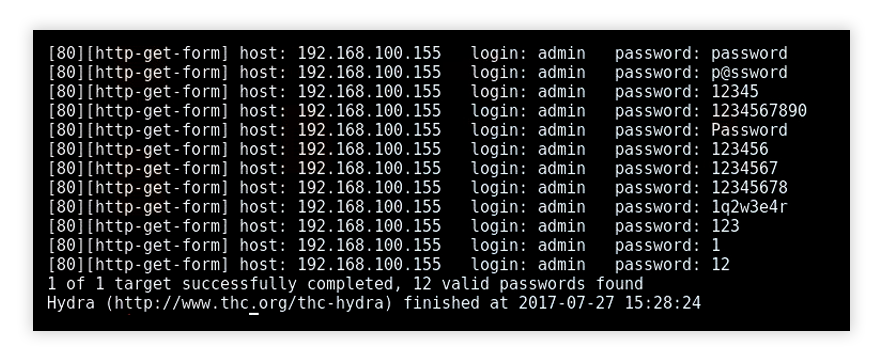
In our case, for decrypting the word we will need to try every possible combination (even like a, aa, b, bb strings and so on).
Now lets calculate how much time is needed to decrypt/check every possible combination for our password. Suppose you own an exceptionally powerful supercomputer, coupled with cutting-edge technology and virtually unlimited resources.
Let’s say the computer has a whopping 1 terabyte (TB) of RAM allowing it to handle lots of tasks at once. For the CPU, this supercomputer boasts a mind-boggling speed of 1 exaflop, which means it can do about 1 quintillion calculations in just one second. 1 exaflop is equal to 1,000,000 gigaflops. So, to achieve 1 exaflop of computing power using Intel i9 processors with a performance of 300 gigaflops each, you would need 1,000,000 gigaflops / 300 gigaflops = 3,333,333 Intel i9 processors.
This hypothetical supercomputer, performing mind-blowing calculations at lightning speed, could do a brute-force attack on an encryption algorithm.
If our hypothetical supercomputer were to attempt every possible combination of text to decipher the encrypted data, it would be faced with an astronomical number of possibilities — ²²⁵⁶. It’s estimated that it would take not just years, not even centuries, but potentially tens of thousands of decades.
To read more about this, you can refer to this article that I wrote.
Randomness in Simulation and Modeling
Monte Carlo Simulation
The Monte Carlo Simulation is a mathematical technique used to understand the impact of risk and uncertainty in prediction and forecasting models. Essentially, it’s a method used to predict the probability of different outcomes when the intervention of random variables is present.
Named after the famous Monte Carlo Casino due to its reliance on randomness, this method is widely used across finance, engineering, research, and more.
In the context of finance, Monte Carlo simulation is commonly used to assess the risk and value of financial instruments, such as options or portfolios. By generating a large number of random scenarios for different input variables, such as asset prices or interest rates, Monte Carlo simulation can provide a range of possible outcomes and their associated probabilities. This method is mostly used when there is no analytical solution for the given problem.
Telecoms use them to assess network performance in various scenarios, which helps them to optimize their networks. Financial analysts use Monte Carlo simulations to assess the risk that an entity will default, and to analyze derivatives such as options. Insurers and oil well drillers also use them to measure risk.
To read more, check out this article.
Future of Randomness in Software Engineering
The future of randomness in software engineering looks particularly promising, with significant advancements expected from emerging technologies like quantum computing.
Quantum Computing and Quantum Randomness
Quantum computing introduces an inherently stochastic element known as quantum randomness.
Unlike classical computing, which relies on deterministic processes, quantum processes are unpredictable by nature. Quantum random number generators (QRNGs) exploit this property to generate true random numbers directly from quantum phenomena, such as the superposition of quantum states or the measurement of entangled particles.
These devices are expected to provide a more secure and fundamentally unpredictable source of randomness than is currently possible.

Quantum computing has the potential to revolutionize cryptography. Current cryptographic systems rely on the computational difficulty of certain problems (like factoring large numbers) which quantum computers could solve effortlessly. But quantum cryptography, utilizing quantum randomness for key distribution, promises to be virtually unbreakable due to the laws of quantum mechanics.
Current State of Quantum Computing
As of now, quantum computing is in an experimental phase. Researchers and companies like Google, IBM, and D-Wave are actively developing quantum computers and have made significant progress in recent years.
For instance, Google announced "quantum supremacy" in 2019, claiming that their quantum computer solved a problem that would be practically impossible for a classical computer to solve in any reasonable amount of time.
Quantum bits, or qubits, which are the basic units of information in quantum computing, are highly susceptible to interference from their environment. This leads to high error rates in quantum computations. Developing error-correcting codes and finding ways to make qubits more stable is a significant focus of current research.
Currently, quantum computers have a limited number of qubits. To be practical for widespread use, quantum computers need to scale up the number of qubits significantly without a corresponding increase in error rates.
Also those computers need to operate at extremely low temperatures, close to absolute zero, to maintain the quantum state of the qubits. Maintaining such conditions is technically challenging and expensive.
The consensus among experts is cautiously optimistic, but varies widely regarding when quantum computing will become practical for broad use.
Some experts believe that within the next decade, we'll begin to see quantum computers solving more practical, real-world problems, potentially revolutionizing fields like cryptography, materials science, and complex system simulation. Others think that these applications might remain out of reach for several more decades.
Wrapping Up
The future of randomness in software engineering holds vast potential to drive innovation across multiple domains.
As we delve deeper into quantum computing and enhance our current technologies, randomness will play an increasingly critical role in shaping the next generation of software solutions, making them more secure, efficient, and reflective of the complex world they model.


