As the name suggests, Pretty Good Privacy (or PGP) is an encryption program that actually provides pretty good privacy. The “pretty good” bit is meant to be a bit of an ironic understatement. It has been one of the dominant forms of end-to-end encryption for email communications after its development by Phil Zimmermann in 1991. It became increasingly popular after its use by whistleblower Edward Snowden.
PGP provides two things essential for a secured communication:
- Confidentiality: Provided through the use of symmetric block encryption, compression using the ZIP algorithm, and E-Mail compatibility using the radix64 encoding scheme
- Authentication: Provided through the use of digital signatures
Without further ado, let us get to the workings of PGP.
How it works
I will be explaining the concept of PGP from the point of view of the implementation in the context of Alice (the sender) and Bob (the receiver). We will be using the following algorithms:
- RSA as the asymmetric encryption algorithm
- SHA-512 as the hashing algorithm
- DES as the symmetric encryption algorithm and
- ZIP for compression
You can use other algorithms as well. (I know DES is too old to be used but the goal here is to understand the concept of PGP.)
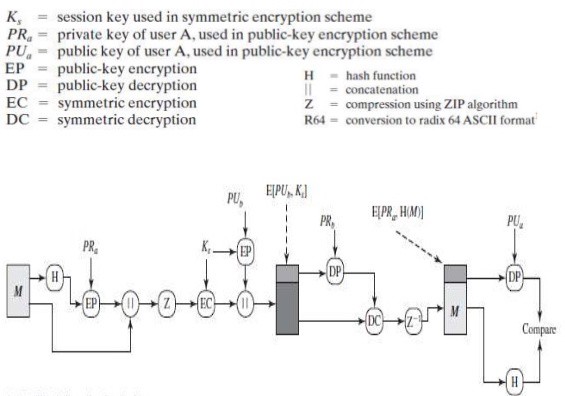
Alice and Bob both generate their pair of keys (Public and Private Keys) using the RSA algorithm. Public keys of Alice and Bob should be known to each other.
Alice’s / Sender’s Side:
- Alice writes a message M, which she intends to send to Bob.
- M is provided as an input to the SHA-512 algorithm to get the 512 bit binary hash (represented as 128 bits hexadecimal string) of it.
- This hash is digitally signed by using RSA algorithm i.e. the hash is encrypted by the private keys of Alice. The inputs to RSA are Private Keys of Alice and the hash. The output from RSA is the digitally signed hash or encrypted hash EH.
- Now, M and EH are appended together. (Appended in the sense that they are put in an array of strings).
- M and EH (which are in an array of strings) act as input to the ZIP compression algorithm to get the compressed M and compressed EH, again in an array of strings.
- The output of the above step is now encrypted using the DES symmetric encryption algorithm. For this, we will first generate the SecretKey for DES. This key and the output of step 5 will act as input to the DES encryption algorithm which will provide us an encrypted output (again in an array of strings).
- Last but not the least, since M is encrypted using SecretKey, it also has to be sent to Bob. We will encrypt the SecretKey of DES algorithm with the Public Key of Bob. We will use RSA for this and the inputs to it will be the Public key of Bob and SecretKey.
- The outputs of steps 6 and 7 are now appended and sent as the final message to Bob.
The whole message is sent as an array of strings (String finalmessage[]) which contains the following at indices:
0: Compressed message M which is encrypted with the SecretKey
1: Digitally signed hash EH which is then compressed and encrypted with the SecretKey
2: Output of step 7
Bob’s / Receiver’s Side:
- Bob will first decrypt the SecretKey of DES with his Private Keys. The inputs to RSA algorithm for this will be Private Keys of Bob and
finalmessage[2]. The output from RSA will give Bob the SecretKey. - This SecretKey will now act as one of the inputs to DES decryption algorithm for decryption of
finalmessage[0]andfinalmessage[1]. These two will also act as the inputs to DES decryption algorithm. The output of this step will bedecrypted versionoffinalmessage[0]andfinalmessage[1]. - The outputs of the above step should be provided as input to the ZIP algorithm for decompression.
- From the output of the above step, we will get the digitally signed hash and the original message M. We will verify whether the hash was signed by Alice. For this, we will calculate the hash of the original message M by using SHA-512 (
calculated_hash). We will also decrypt the digitally signed hash with the public keys of Alice by using RSA.(Inputs to RSA: digitally signed hash and public keys of Alice and Output from RSA:decrypted_hash). - Compare the
decrypted_hashandcalculated_hash. If they turn out to be the same, then authentication is achieved which means that the message was indeed sent by Alice.
The following is the simulation of PGP done in the simplest way using Java.
import java.util.*;
import java.math.*;
import javax.crypto.Cipher;
import java.security.*;
import javax.crypto.KeyGenerator;
import javax.crypto.SecretKey;
import java.io.BufferedReader;
import java.io.ByteArrayInputStream;
import java.io.ByteArrayOutputStream;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.zip.GZIPInputStream;
import java.util.zip.GZIPOutputStream;
import javax.crypto.spec.*;
public class PGP{
static Cipher ecipher, dcipher;//Required for DES
public static void main(String args[]) throws Exception{
//Generating sender keys
KeyPair senderkeyPair = buildKeyPair();
PublicKey senderpubKey = senderkeyPair.getPublic();
PrivateKey senderprivateKey = senderkeyPair.getPrivate();
//Generating receiver keys
KeyPair receiverkeyPair = buildKeyPair();
PublicKey receiverpubKey = receiverkeyPair.getPublic();
PrivateKey receiverprivateKey = receiverkeyPair.getPrivate();
//Sending both public keys and private keys for choice of digital signature or normal assymetric encryption
String messagetoreceiver[] = senderside(senderpubKey, senderprivateKey, receiverpubKey, receiverprivateKey);
receiverside(messagetoreceiver, senderpubKey, senderprivateKey, receiverpubKey, receiverprivateKey);
}
public static void receiverside(String messagetoreceiver[], PublicKey senderpubKey, PrivateKey senderprivateKey, PublicKey receiverpubKey, PrivateKey receiverprivateKey) throws Exception {
//Receiver receives the message messagetoreceiver[] with messagetoreceiver[2] as secret key encrypted with receiver pub key
//Receiver decrypts the messagetoreceiver[2] with his/her privatekey
String receiverencodedsecretkey = decrypt(receiverpubKey, receiverprivateKey, messagetoreceiver[2], 1);
//Key after decryption is in base64 encoded form
byte[] decodedKey = Base64.getDecoder().decode(receiverencodedsecretkey);
SecretKey originalKey = new SecretKeySpec(decodedKey, 0, decodedKey.length, "DES");
System.out.println("\nReceiver Side: Receiver SecretKey DES after Decryption with his/her Private Key=\n"+originalKey.toString());
//Decrypt the rest of the message in messagetoreceiver with SecretKey originalKey
String receiverdecryptedmessage[] = new String[messagetoreceiver.length-1];
System.out.println("\nReceiver Side: Message After Decryption with SecretKey=");
for (int i=0;i<messagetoreceiver.length-1;i++) {
messagetoreceiver[i] = decryptDES(messagetoreceiver[i], originalKey);
System.out.println(messagetoreceiver[i]);
}
//Unzip this message now i.e. unzip messagetoreceiver
String unzipstring[] = new String[receiverdecryptedmessage.length];
System.out.println("\nReceiver Side: UnZipped Message=");
for (int i=0;i<unzipstring.length;i++) {
unzipstring[i] = decompress(messagetoreceiver[i]);
System.out.println(unzipstring[i]);
}
//Message has been received and is in unzipstring but check the digital signature of the sender i.e. verify the hash with senderpubkey
//So decrypting the encrypted hash in unzipstring with sender pub key
String receivedhash = decrypt(senderpubKey, senderprivateKey, unzipstring[1], 0);
System.out.println("\nReceiver Side: Received Hash=\n"+receivedhash);
//Calculating SHA512 at receiver side of message
String calculatedhash = sha512(unzipstring[0]);
System.out.println("\nReceiver Side: Calculated Hash by Receiver=\n"+calculatedhash);
if (receivedhash.equalsIgnoreCase(calculatedhash)) {
System.out.println("\nReceived Hash = Calculated Hash\nThus, Confidentiality and Authentication both are achieved\nSuccessful PGP Simulation\n");
}
}
public static String[] senderside(PublicKey senderpubKey, PrivateKey senderprivateKey, PublicKey receiverpubKey, PrivateKey receiverprivateKey) throws Exception {
//Input from user
System.out.print("\nPGP Simulation:\nSender Side: Input messsage=\n");
Scanner sc = new Scanner(System.in);
String rawinput;
rawinput = sc.nextLine();
//Generating SHA-512 hash of original message
String hashout = sha512(rawinput);
System.out.println("\nSender Side: Hash of Message=\n"+hashout);
//Encrypt the message hash with sender private keys -> Digital Signature
String encryptedprivhash = encrypt(senderpubKey, senderprivateKey, hashout, 0);
System.out.println("\nSender Side: Hash Encrypted with Sender Private Key (Digital Signature)=\n"+ encryptedprivhash);
//Append original message and encrypted hash
String beforezipstring[] = {rawinput, encryptedprivhash};
System.out.println("\nSender Side: Message before Compression=\n"+beforezipstring[0]+beforezipstring[1]);
//Apply zip to beforezipbytes[][]
String afterzipstring[] = new String[beforezipstring.length];
System.out.println("\nSender Side: Message after Compression=");
for (int i=0;i<beforezipstring.length;i++) {
afterzipstring[i] = compress(beforezipstring[i]);
System.out.println(afterzipstring[i]);
}
//Encrypt zipstring with DES
SecretKey key = KeyGenerator.getInstance("DES").generateKey();
System.out.println("\nSender Side: SecretKey DES=\n"+key.toString());
String afterzipstringDES[] = new String[afterzipstring.length+1];
System.out.println("\nSender Side: Compressed Message Encrypted with SecretKey=");
for (int i=0;i<afterzipstring.length;i++) {
afterzipstringDES[i] = encryptDES(afterzipstring[i], key);
System.out.println(afterzipstringDES[i]);
}
//Encrypt DES key with Receiver Public Key using RSA
String encodedKey = Base64.getEncoder().encodeToString(key.getEncoded());
//SecretKey is base64 encoded since direct string enccryption gives key in string format during decryption which cant be converted to SecretKey Format
String keyencryptedwithreceiverpub = encrypt(receiverpubKey, receiverprivateKey, encodedKey, 1);
System.out.println("\nSender Side: DES SecretKey Encrypted with Receiver Public Key=\n"+keyencryptedwithreceiverpub);
//Decrypting DES key with Receiver Private Key using RSA
afterzipstringDES[2]=keyencryptedwithreceiverpub;
String messagetoreceiver[] = afterzipstringDES;
System.out.println("\nFinal Message to receiver=");
for (int i=0;i<messagetoreceiver.length;i++) {
System.out.println(messagetoreceiver[i]);
}
return messagetoreceiver;
}
public static String encryptDES(String str, SecretKey key) throws Exception {
ecipher = Cipher.getInstance("DES");
ecipher.init(Cipher.ENCRYPT_MODE, key);
// Encode the string into bytes using utf-8
byte[] utf8 = str.getBytes("UTF8");
// Encrypt
byte[] enc = ecipher.doFinal(utf8);
// Encode bytes to base64 to get a string
return new sun.misc.BASE64Encoder().encode(enc);
}
public static String decryptDES(String st, SecretKey key) throws Exception {
dcipher = Cipher.getInstance("DES");
dcipher.init(Cipher.DECRYPT_MODE, key);
// Decode base64 to get bytes
byte[] dec = new sun.misc.BASE64Decoder().decodeBuffer(st);
byte[] utf8 = dcipher.doFinal(dec);
// Decode using utf-8
return new String(utf8, "UTF8");
}
public static String decompress(String st) throws IOException {
byte[] compressed = new sun.misc.BASE64Decoder().decodeBuffer(st);
ByteArrayInputStream bis = new ByteArrayInputStream(compressed);
GZIPInputStream gis = new GZIPInputStream(bis);
BufferedReader br = new BufferedReader(new InputStreamReader(gis, "UTF-8"));
StringBuilder sb = new StringBuilder();
String line;
while((line = br.readLine()) != null) {
sb.append(line);
}
br.close();
gis.close();
bis.close();
return sb.toString();
}
public static String compress(String data) throws IOException {
ByteArrayOutputStream bos = new ByteArrayOutputStream(data.length());
GZIPOutputStream gzip = new GZIPOutputStream(bos);
gzip.write(data.getBytes());
gzip.close();
byte[] compressed = bos.toByteArray();
bos.close();
return new sun.misc.BASE64Encoder().encode(compressed);
}
//Takes any string as input and calculates sha 512 bit hash. Output is in 128 bit hex string
public static String sha512(String rawinput){
String hashout = "";
try{
MessageDigest digest = MessageDigest.getInstance("SHA-512");
digest.reset();
digest.update(rawinput.getBytes("utf8"));
hashout = String.format("%040x", new BigInteger(1, digest.digest()));
}
catch(Exception E){
System.out.println("Hash Exception");
}
return hashout;
}
public static KeyPair buildKeyPair() throws NoSuchAlgorithmException {
final int keySize = 2048;
KeyPairGenerator keyPairGenerator = KeyPairGenerator.getInstance("RSA");
keyPairGenerator.initialize(keySize);
return keyPairGenerator.genKeyPair();
}
//n: 0->encryptwithprivatekey 1->encryptwithpublickey
public static String encrypt(PublicKey publicKey, PrivateKey privateKey, String message, int ch) throws Exception {
Cipher cipher = Cipher.getInstance("RSA");
if (ch == 0) {
cipher.init(Cipher.ENCRYPT_MODE, privateKey);
byte[] utf8 = cipher.doFinal(message.getBytes("UTF-8"));
return new sun.misc.BASE64Encoder().encode(utf8);
}
else {
cipher.init(Cipher.ENCRYPT_MODE, publicKey);
byte[] utf8 = cipher.doFinal(message.getBytes("UTF-8"));
return new sun.misc.BASE64Encoder().encode(utf8);
}
}
//n: 0->decryptwithpublickey 1->decryptwithprivatekey
public static String decrypt(PublicKey publicKey,PrivateKey privateKey, String st, int ch) throws Exception {
Cipher cipher = Cipher.getInstance("RSA");
byte[] encrypted = new sun.misc.BASE64Decoder().decodeBuffer(st);
if (ch == 0) {
cipher.init(Cipher.DECRYPT_MODE, publicKey);
byte[] utf8 = cipher.doFinal(encrypted);
return new String(utf8, "UTF8");
}
else {
cipher.init(Cipher.DECRYPT_MODE, privateKey);
byte[] utf8 = cipher.doFinal(encrypted);
return new String(utf8, "UTF8");
}
}
}We have used the base64 encoding scheme which is similar to radix64 that is used in PGP.
Note:
- We base64 encode the strings after encryption and compression so as to get a readable text form.
- For decryption and decompression, we send the base64 decoded inputs as the actual inputs to the decryption and decompression algorithms.
- The key has been base64 encoded and decoded since I have used Java for simulation of PGP, which requires encoded form at the receiver side so that it can be converted to SecretKey datatype for decryption process.
Please follow, clap and share. Comment for any mistakes or improvements or suggestions. You can even follow me on Twitter.
