A brief note - this article is about the theory of how to crack hashed passwords. Understanding how cybercriminals execute attacks is extremely important for understanding how to secure systems against those types of attacks.
But attempting to hack a system you do not own is likely illegal in your jurisdiction (plus hacking your own systems may [and often does] violate any warranty for that product).
This article assumes some level of knowledge of hashing functions and basic password cracking techniques - if you don't understand those topics, check out these articles.
So, you've obtained a set of hashed passwords. Brute forcing the hash will take a very long time. How can you speed up this process?
Wait, I thought hash functions were one-way! How do you crack hash functions?
Unfortunately, the hashing functions which are used for hashing passwords aren't always as secure as generally approved hash functions. For example, the hashing function used for old Windows devices is known as LM Hash, which is so weak that it can be cracked in a few seconds.
Also, you don't need to reverse engineer the hash. Instead, you can use a pre-computed set of plaintext passwords and the corresponding hash value (<password>, <hash>). This tells a hacker what plaintext value produces a specific hash.
With this you'll know what plaintext value produces the hash you're looking for. When you enter a password the computer will hash this value and compare it to the stored value (where it will match) and you'll be able to authenticate. Thus, you don't actually need to guess someone's password, just a value which will create the same hash.
This is called a collision. Essentially, as a hash can take data of any length or content, there are unlimited possibilities for data which can be hashed.
Since a hash converts this text into a fixed length content (for example, 32 characters), there are a finite number of combinations for a hash. It is a very very large number of possibilities, but not an infinite one.
Eventually two different sets of data will yield the same hash value.
Precomputed tables are very helpful in achieving this, as they save significant time and computing power. Using a pre-computed set of hashes to look up a password hash is called a 'lookup-table attack'. These tables are used by system administrators to test the strength of their users' passwords, and are often available online or for purchase. However, they can also be used by nefarious hackers.
If a password is insecure (let's say someone uses a password 5 characters long), it can be relatively easily cracked. For example, a password of 5 lowercase characters can only be used to create 11,881,376 different passwords (26^5).
For a hash of this password, even if the hash is cryptographically secure (uses an appropriate algorithm), it would still be very easy to compute all possible passwords and their corresponding hashes. Lookup tables work very well for these types of password hashes.
However, as passwords increase in length, the storage (and therefore storage cost) you need for every possible password and the corresponding hash grows exponentially.
For example if the password you're trying to crack is 8 characters long but uses numbers (10 digits), lowercase letters (26), uppercase letters (26), and some special characters (10), the number of possible passwords jumps to 722,204,136,308,736 - which is A LOT of storage space, when you realize each is hashed with a hashing function like SHA-256.
Rainbow tables address this issue by offering reduced storage needs, but they take more time to compute the potential passwords. At the most basic level, these are essentially pre-computed lookup tables which enable you to quickly find the plaintext which matches the hash you have. If the hash and plaintext are contained in the table you have - similar to dictionary attacks - you're only looking to see if the password is contained in the table you have. If it isn't, you won't be able to crack the password. You can find these online for free or for purchase.
Check out this article for a tutorial on creating your own rainbow tables.
I'm still interested. How do rainbow tables work?
If you want to skip the detailed explanation of how these work, feel free to scroll down to the 'How to protect against these attacks' section.
In order to save yourself from hashing and storing each possible plaintext until you find the hash you need (like a lookup table), you hash each plaintext and store the result in a table to look up later without having to regenerate them. This takes longer, but saves memory.
To generate the table, you create 'chains' of hashes and plaintext using a hashing function and a reduction function. A reduction function just creates plaintext from a hash (it doesn't reverse engineer the hash, but rather creates different plaintext from the hash). It is also a one-way function.
Thus in order to compute the table, you use one of your hashes, h1, in your reduction function, R(), in order to create the plaintext p1.
R(h1) = p1.
Then you use the hash function H() with p1 to create a new hash.
H(p1) = h2.
Using our example from before:
If the set of plaintext is [abcdefghijklmnopqrstuvwxyz]{5} (we're looking for a rainbow table of all passwords composed of lowercase letters of length 5) and we're using MD5 (a hashing algorithm):
A hash might be ab56b4d92b40713acc5af89985d4b786 (h1). Now, we apply the reduction function, which could be as simple taking the last 5 letters in the hash.
R(ab56b4d92b40713acc5af89985d4b786) = cafdb
H(cafdb) = 81a516edabf924cd0f727d329e855b1f
Why are they called rainbow tables?
Each column uses a different reduction function. So if each column were colored, it would be a very long, skinny rainbow.
Using different reduction functions reduces the number of chain merges (collisions) which happened frequently with hash-chains, the predecessor to rainbow tables. This essentially means that if you keep using the same reduction function, there's a chance you'll end up with two different chains which converge to the same plaintext. Using different reduction functions reduces the chance of this happening, though it isn't impossible.
Great, how do you create a chain?
In order to create a chain, you're using your reduction function and hashing function (both one way) to create a 'chain' of hashes and plaintext. Each of these 'chains' would continue for k steps, and when the chain ends, will store only the first plaintext and the last hash in the chain.
So, a sample chain looks like this:
p1 -> h1 = H(p1) -> R1(h1) = p2 -> H(p2) = h2 -> R2(h2) = p3 -> H(p3) = h3
Each reduction function is different (represented by R1, R2, R3, etc.) A sample table of chains (each row is a chain of length 5) looks like the following. Note that this is populated with fake data just to give you an example - the hashing function isn't a hash function you would find used to hash passwords.
The reduction functions, R1 and R2 are defined as follows – R1 takes the first 3 digits of the hash, and R2 takes the last 2 letters of the hash:
p1 -> h1 = H(p1) -> R1(h1) = p2 -> H(p2) = h2 -> R2(h2) = p3 -> H(p3) = h3
2 -—> abdu2934 -—> 293 -—> 83kdnif8 -—> if -—> ike83jd3
15 -—> dks2ne94 -—> 294 -—> ld932nd9 -—> ld -—> ldie938d
20 -—> ld93md8d -—> 938 -—> lxked93k -—> lx -—> 93mdkg8d
In a rainbow table, only the first starting point and the endpoint are saved to save on storage, like this:
starting point (plaintext) endpoint, after k steps through the chain (hash)
p1 -—> h1k
p2 -—> h2k
p3 -—> h3k
Then when you have a hash (h) where you don't know the plaintext (?), you'll compare it to the chains.
- First, you'll check if the hash is in the list of final hashes (h1k, h2k, etc.). If so, you can move to step 3.
- If not, you can reduce the hash to different plaintext (R1) and then hash that plaintext (using the hash function and next reduction function above) and compare it to the list of final hashes (h1k, h2k, h3k, etc.). When it matches one of the final hashes, that chain will likely contain the original hash.
- In order to find the original hash in the chain, take that chain's starting plaintext (so if it matches h1k, start with p1) and apply the hashing and reduction functions to move along the chain until you reach the known hash and its corresponding plaintext. This way you can move through the hashes in the chain without having them take up storage space on your machine.
While you can't be sure that the chains will contain the hash you need, the more chains you've generated (or are referencing) the more certain you can be. Unfortunately, each chain is time-intensive to generate, and increasing the number of chains increases the time you need.
How do you defend against these types of attacks?
First, a layered defense of all systems. If you can prevent compromise of your systems via other methods (so the attacker can't get a copy of your hashed passwords), the attacker won't be able to crack them.
You can also use salting, which adds a random value to the password before encrypting it. That means that the precomputed value you've found (which matches the hash) won't work. The encrypted text is not based solely on the unencrypted text. Because the salt is different for each password, each needs to be cracked individually.
Salting is now included in most major hash types as an option. While Windows doesn't currently use salting, they can encrypt stored hashes if you use the 'SYSKEY' tool.
You can also use 'rounds', or hashing a password multiple times. Using rounds (particularly if the number of rounds is randomly chosen for each user), makes the hacker's job harder. This is most effective when combined with salting.
Unfortunately, a hacker who has the hashed passwords will have also have access to the number of rounds used and the salt used (because in order to get that list they've probably compromised . The salt and number of rounds used is stored with the password hash, meaning that if the attacker has one, they also have the other. However, they won't be able to use precomputed rainbow tables available online, and will have to compute their own tables (which is extremely time consuming).
One other method designed to increase the difficulty of cracking the password is to use a pepper. Pepper is similar to salt, but while a salt is not secret (it's stored with the hashed password), pepper is stored separately (for example, in a configuration file) in order to prevent a hacker from accessing it. This means the pepper is secret, and its effectiveness depends on this.
Pepper needs to be different for each application it is used for, and should be long enough to be secure. At least 112 bits is recommended by the National Institute of Standards and Technology.
While using a pepper can be effective in some cases, there are some downsides. First, no current algorithm supports peppers, which means practically, this is impossible to implement at scale. That is, unless you're creating your own algorithms. Listen to Bruce Schneier. Don't do that.
For a longer article on the problems with peppers, check out this thread.
Finally, use strong (at least 12 character), complex passwords, and implement strong password policies across all systems. This can include forcing users to create strong passwords, testing their strength regularly, using password managers on an enterprise level, enforcing use of 2FA, and so on.
Confused about what makes a strong password?
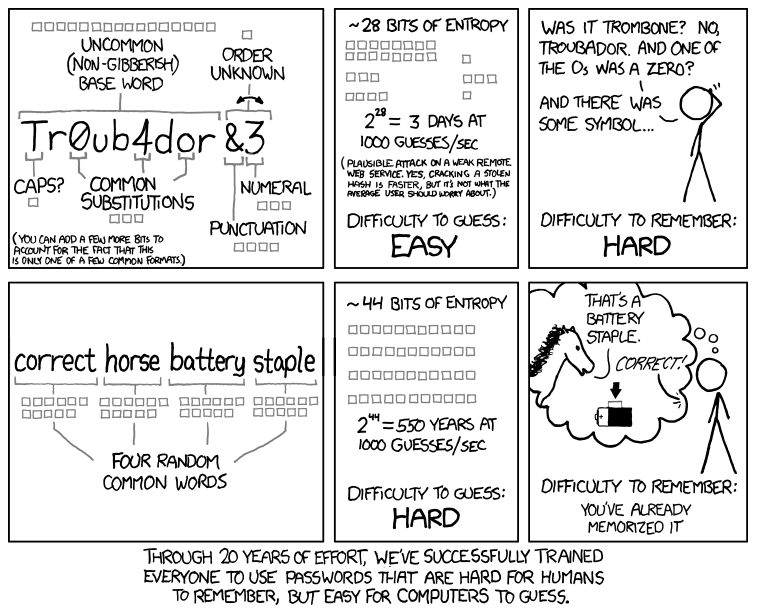
It seems really easy to get hacked. Should I be concerned?
The most important thing to remember about hacking is that no one wants to do more work than they have to do. For example, calculating rainbow tables is a lot of work. If there's an easier way to get your password, that's probably what a nefarious actor will try first (like phishing!).
That means that enabling basic cyber security best practices is probably the easiest way to prevent getting hacked. In fact, Microsoft recently reported that just enabling 2FA will end up blocking 99.9% of automated attacks.

Happy hacking!
Additional Reading:
Another explanation of rainbow tables
A list of rainbow tables online

