You might remember this simple mantra from your statistics class:
"Correlation does not imply causation."
So maybe you think you know what this phrase means.
Like, if you studied really hard in statistics, got a good grade, and then got into college, it must mean that you got into college because you aced Statistics class.
While that grade, along with the skills you learned, probably helped, you can't ignore the other factors at play - and likely can't argue that your Stats grade was the cause of your acceptance into college.

First things first - why do we mistake correlation with causation?
It's easy to think that just because two things seem related, that one must be the cause of the other. But that can be a foolish and sometimes dangerous assumption.
For example, suppose you're trying to figure out what makes people less grumpy. You perform a study which finds that, when people get at least x hours of sleep a night, they're less grumpy.
But have you taken all factors into account here? Perhaps they also started working out more as a consequence of being well-rested, and this is what altered their moods.
Not all examples are quite so benign - and some are downright nonsensical.
To illustrate how misleading it can be to assume that correlation implies causation, have a look at the following graph from Tyler Vigen's Spurious Correlations:
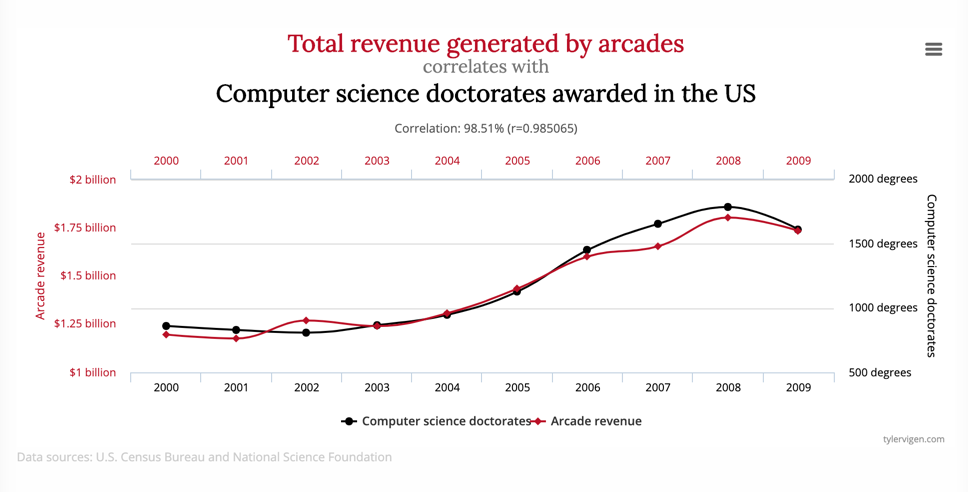
While there happens to be a strong correlation between these two factors, I doubt you could effectively argue that one caused the other. Perhaps this will be a challenge for people to try and prove.
Here's another gem from Tyler's collection:
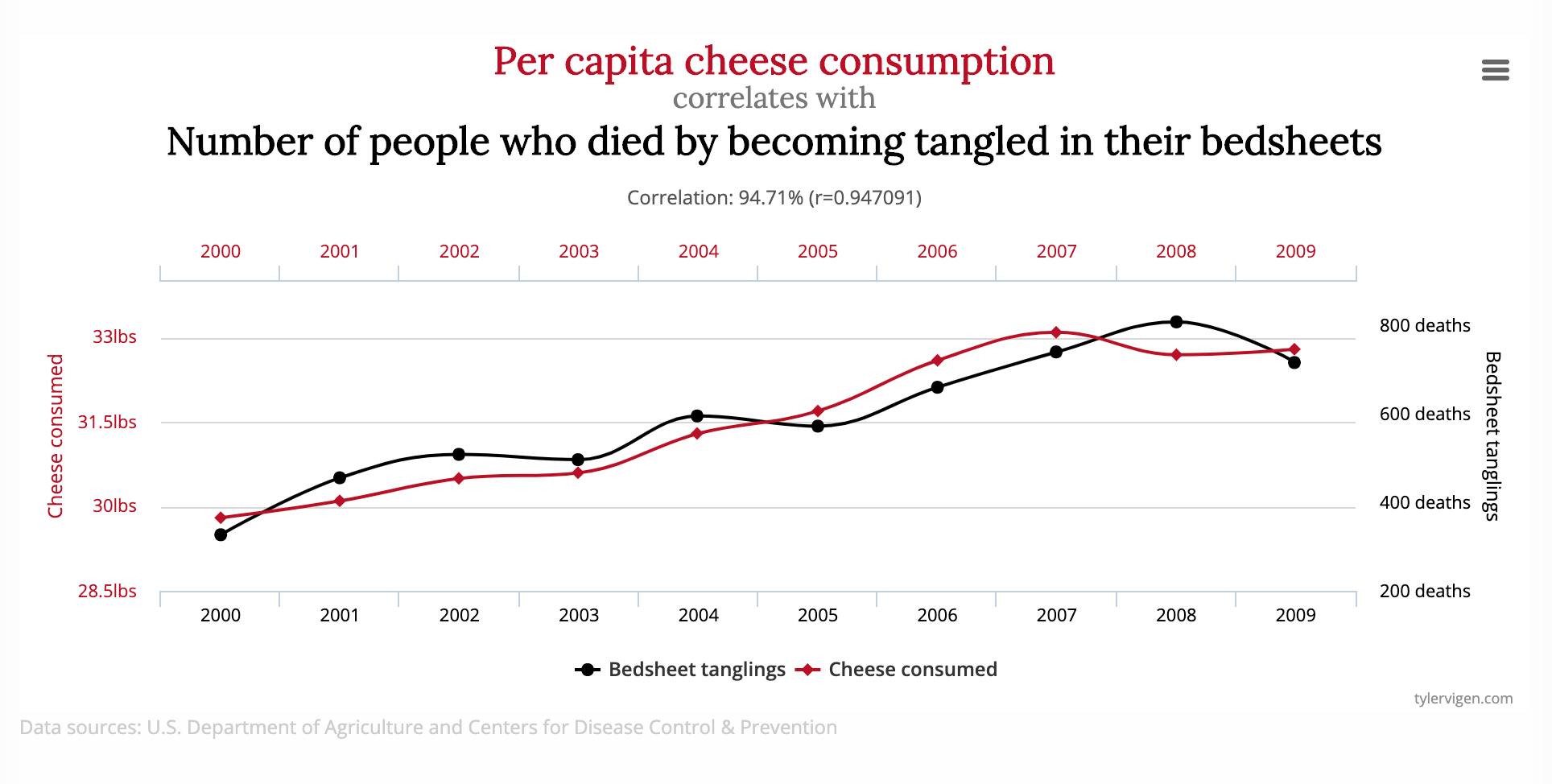
Look at that beautiful correlation. But you'd be hard pressed to argue that, just because someone ate more cheese, they'd be more likely to fatally entangle themselves in their bed sheets.
What is correlation in statistics?
According to the dictionary, a correlation is a mutual relationship or connection between two or more things (or variables) - especially one that is not expected on the basis of chance alone.
Let's use it in a sentence: The huge size of my homegrown tomatoes seems to correlate with the extra rain we had this summer.
Now, here I'm assuming that, because it rained a bit more than usual, my tomato plants went nuts and produced monster tomatoes.
But is that the only factor? What about the nutrient rich compost I used in my raised beds? What about the quality of the plants I bought from the nursery? What about my careful pruning and tending?
As you can see, although there is correlation between my large tomatoes and our rainy summer, this doesn't necessarily imply causation.
What is causation in statistics?
Time for another definition. Causation, according to the dictionary, is the act or agency which produces an effect.
Let's get a bit more specific. Causation means that there is a relationship between two events where one event affects the other. In statistics, when the value of an event - or variable - goes up or down because of another event or variable, we can say there was causation. A caused B to happen.
How about an example for this one? Perhaps you freelance for a magazine that pays by the word. The longer the story (and the more words it contains), the more you get paid.
So there's a direct correlation between how many words you write and how much you get paid. But there's also causation (because you wrote more, you got paid more).
Why is it so easy to get this wrong?
Why is it so easy to think that correlation implies causation? Well, if two things seem related, we tend to associate them and assume they impact each other. When the weather's cold, people spend more time inside. Around the holidays, shopping malls are packed. When you take some ibuprofen, your headache goes away.
While these circumstances certainly are related - and some might even imply causality - they don't necessarily stand up to scientific analysis.
There are a few reasons we might mistakenly infer causation from correlation.
What is a Confounding Variable?
First of all, you might have a confounding variable in the mix. This is a variable that affects both the independent and dependent variables in your relationship - and so confounds your ability to determine the nature of that relationship.
For example, if a new family moves into a neighborhood, and crime goes up, the residents in that area might assume it's because of that new family. But what if, at the same time, a detention center opened nearby? That's the more likely cause of the increased crime.
What is Reverse Causation?
Second, you might be dealing with reverse causation. This happens when, instead of correctly assuming that A causes B, you get them mixed up and assume that B causes A.
It might be hard to imagine how this happens, but think of how solar panels work. They produce more power when the sun is in the sky longer.
But the sun isn't in the sky longer because the panels are producing more power. The panels are producing more power because the sun shines for longer periods of time.
What is a Coincidence?
Third, we must not forget the power of coincidence. When two things happen to occur at the same time, it's tempting to see causation. But just like that silly graph above, with the arcades and CS degrees, many are just coincidences.
In the end - why do we care?
Perhaps you're trying to figure out whether a certain new drug makes patients feel better. Or you'd like to know what makes people buy a certain product.
Whatever your motivation, it's often very useful to figure out whether A causes B, along with how and why.
But as we've seen, it's not that easy. You've got to control as many factors as you can, reduce the likelihood of confounding variables and coincidences, and pare down the data to what's relevant.
We won't get into the deeper philosophical question of how we can really establish causation without a doubt. That's for another time.
At least now you know that - even though two events or variables may seem related - it doesn't mean that one has a direct causal affect on the other.

