by Yung L. Leung
Linear data structures are simple in direction. A linked list is a list of nodes (each containing their own data) that are linked from one node to the next (and to the previous, for a doubly linked list). A stack builds upward like a tower of data. Each node stacking atop another, and shortens in a last in first out (LIFO) manner. A queue is a line of nodes that elongate from the end of the line and shortens in a first in first out (FIFO) mechanism.
Binary data structures are like a fork in a road of data. The nodes build like the branches of a tree or a heap of rocks.
Trees

A binary search tree is made up of nodes that branch off to no more than two nodes (binary). A parent node can have left and right child nodes. By convention, left child nodes contain values less than the parent. Whereas right child nodes contain greater values (left is less, right is greater). All trees begin with a single root node.
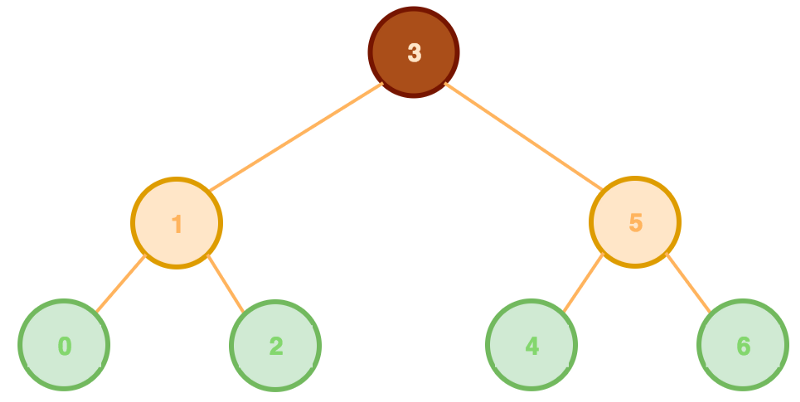
To insert a value requires creating a new node, comparing its value to the root & its descendant values, while deciding to search further leftward (insertion of lesser value) or rightward (insertion of greater value). Once an available position is found, the node is inserted in place.

To find a value is similar to the insertion of a value. You are performing the search for a stored value and returning the node containing it.

To make a breadth-first search of values requires storing a root value. Then proceeding with the left child, then the right child and so forth.

To make a depth-first search (pre-order) of values requires storing a root value. Then proceeding with all leftward descendants, before the rightward descendants.

Since inserting & finding a node of some value are relatively similar processes (insertion inserts a node whereas finding returns a node), it is of no surprise that their complexity is the same, O(log n).
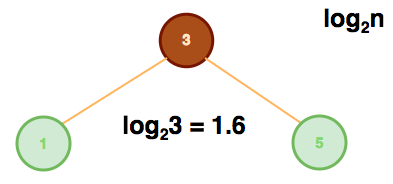
For a 3 node binary search tree, to find 5 requires two steps:
- Is 5 greater than or less than 3? Proceed rightward.
- Is 5 equal to the value being searched? Return node.
Similarly to insert a node with value 6 requires two steps:
- Is 6 greater than or less than 3? Proceed rightward.
- Is 6 greater than or less than 5? Insert the right side.
Heaps

A binary heap is a pyramidal structure of nodes whose nodes can stack upward with rows of decreasing values toward a minimum (minimum binary heap) or with rows of increasing values toward a maximum (maximum binary heap). Like the tree, each parent node can extend up to two child nodes. Unlike the tree, each parent can contain a lesser value than its children (minimum binary heap) or a greater value (maximum binary heap).
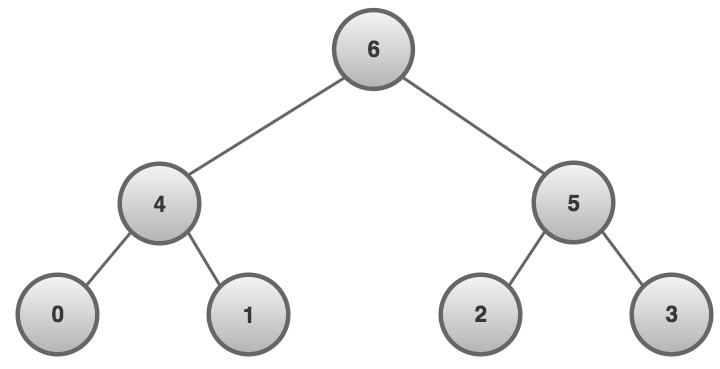
For a max binary heap, to insert a value at the base of the pyramid requires comparing it to parent nodes and bubbling up the larger value.

To extract a max value requires removing the apex value and sinking down a value from the pyramid’s base. This involves finding the higher of the two children nodes.

For a max binary heap, insertion of a node & extraction of a node with the max value both has a complexity of O(log n).
For a 3 node max binary heap, insertion of a node with value 6 requires two steps.
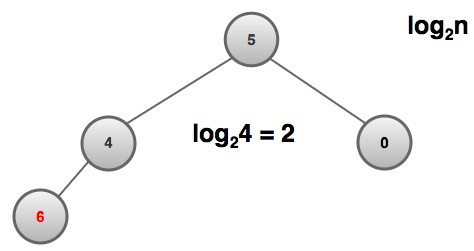
- Upon attaching node of value 6 to a new row (below 4), is 6 greater than or less than 4? Swap.
- Is 6 greater than or less than 5? Swap.
Similarly, after the removal of a node with a max value & replacing it with a node of value 1, two steps remain.
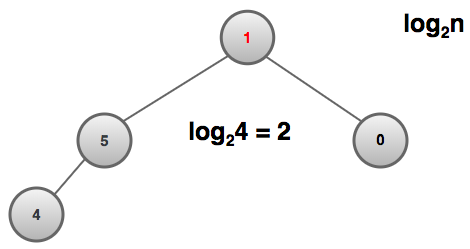
- Is 1 greater than or less than 5? Swap.
- Is 1 greater than or less than 4? Swap.
Thank you for reading!
Reference:
https://www.udemy.com/js-algorithms-and-data-structures-masterclass/
