Get to know the data structures that you use every day
👋 Welcome! Let’s Start with Some Vital Context. Let me ask you something:
✅ Do you use Google Search?
✅ Do you use Google Maps?
✅ Do you use social media sites?
If your answer is “yes” to any of these questions, then you’ve definitely used graphs and you didn’t even know it! Surprised? 😲 I was, too! This article will give you a visual introduction to the world of graphs, their purpose, elements, and types.
These data structures really caught my attention due to their amazing capabilities. They are so powerful that you won’t even imagine how diverse their real-world applications can be. Let’s begin! 😁
🌐 Real-World Applications — The Magic Begins!
Graphs are used in diverse industries and fields:
- GPS systems and Google Maps use graphs to find the shortest path from one destination to another.
- Social Networks use graphs to represent connections between users.
- The Google Search algorithm uses graphs to determine the relevance of search results.
- Operations Research is a field that uses graphs to find the optimal path to reduce the cost of transportation and delivery of goods and services.
- Even Chemistry uses graphs to represent molecules!!! ❤️
Their applications are amazing, right?
Let’s start our journey through this world! 😄
🔵 Meet Graphs!
Now that you have some context, let’s start by talking about their main purpose and elements.
Graphs are used to represent, find, analyze, and optimize connections between elements (houses, airports, locations, users, articles, etc.).
This is an example of what a graph looks like:
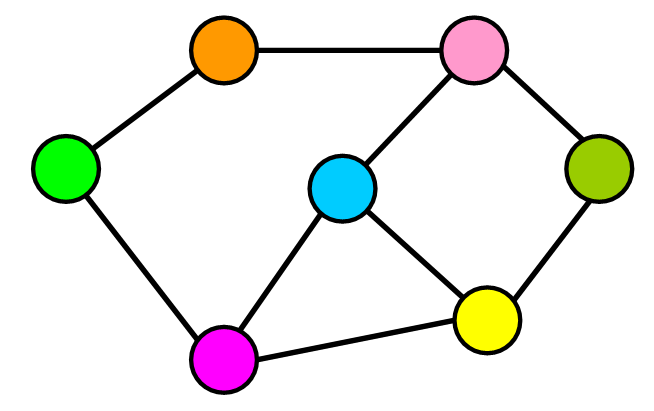
💠 Building-Blocks
I’m sure that you noticed two main elements in the diagram above: circles and thick lines connecting them. They are called, respectively, Nodes and Edges.
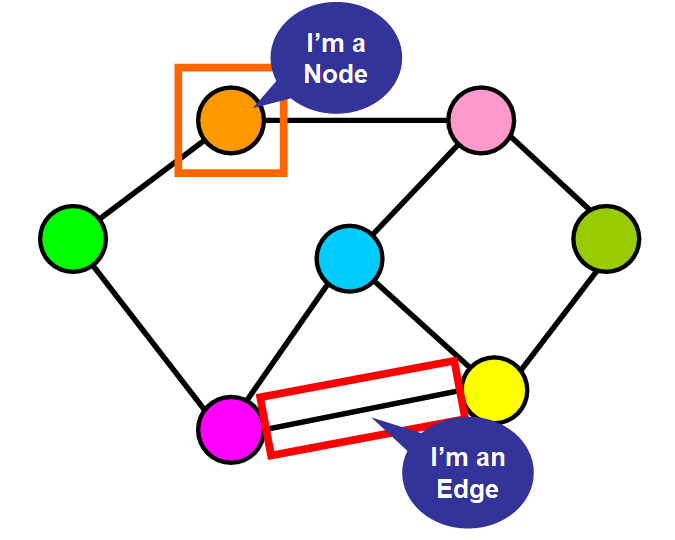
Let’s see them in more detail! 👍
- Nodes: they are the elements that create the network. They could represent houses, locations, airports, ports, bus stops, buildings, users, basically anything that you could represent as being connected to other similar elements in a network.
- Edges: they are connections between the nodes. They could represent streets, flights, bus routes, a connection between two users in a social network, or anything that could possibly represent a connection between the nodes in the context that you are working with.
😱 What Happens If There Is No Connection?
If two nodes are not connected by an edge, that means that there is no direct connection between them. But don’t panic! 😩 You might still be able to go from one node to another by following a sequence of edges, similar to driving through several streets to reach your final destination. 🚛️ 🚛 🚛
For example, in the diagram below, even though there is no direct connection (edge) between the purple node (left) and the yellow node (right), you can go from the purple node to the orange node, to the pink node, to the green node, and finally reach the yellow node. 🏁
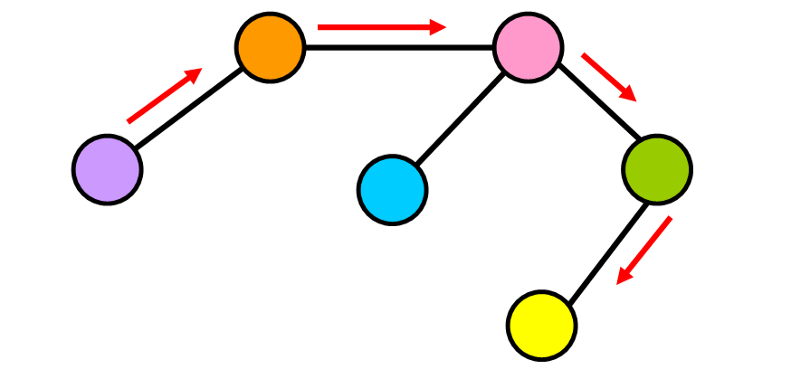
This is a key aspect of graphs, that you can search for the element that you are looking for by following the paths available.
🌟 Notation & Terminology
It’s very important to learn the formal “language” to work with graphs:
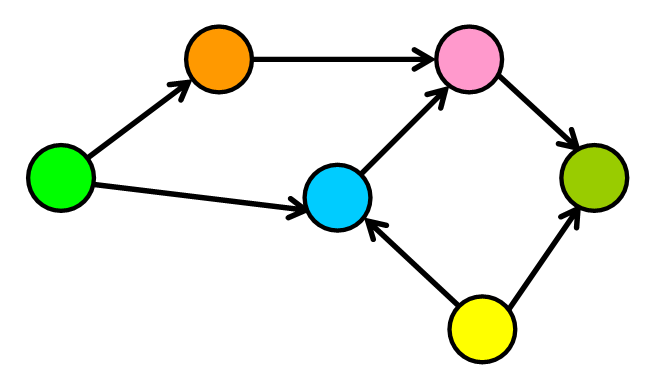
|V|= Total number of vertices (nodes) in the graph.|E|= Total number of connections (edges) in the graph.
In the example below, |V| = 6 because there are six nodes (circles) and|E| = 7 because there are seven edges (lines).
📚 Types of Graphs
Graphs are classified based on the characteristics of their edges (connections). Let’s take a look them in detail! 😃
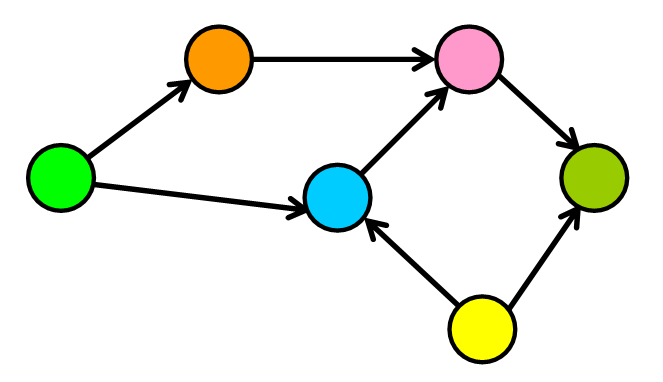
1️⃣ Directed Graphs
In directed graphs, edges have a direction. They go from one node to another, and there is no way to return to the initial node through that edge.
As you can see in the diagram below, the edges (connections) now have arrows that point to a specific direction. Think of these edges as one-way streets. You can go in one direction and reach your destination, but you can’t return through that same street, so you need to find an alternative path.
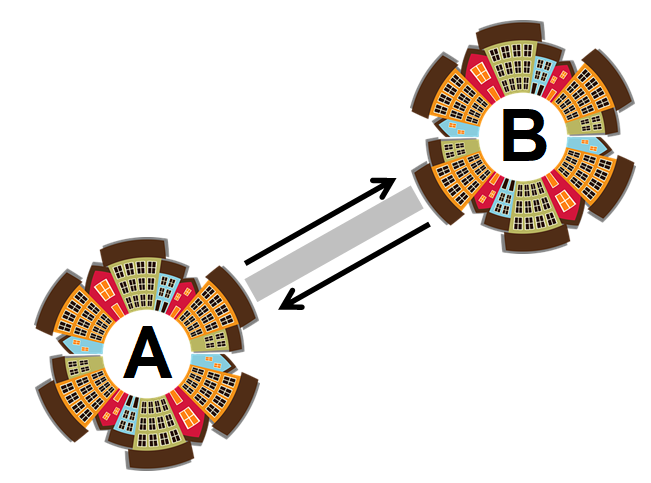
🍕 For example, if we create a graph for a pizza delivery service, representing a city, two houses (nodes) may be connected by a one-way street (edge). You could get from house A to house B through this street, but you couldn’t go back, so you would have to take an alternative path.
💡 Note: In a directed graph, you may not be able return at all to your initial location if there is no path with the appropriate directions. 😞 In the diagram below, you can see that you can successfully go from the purple node to the green node, but notice that there is no way to return from the green node to the purple node because the edges are “one-way streets.”
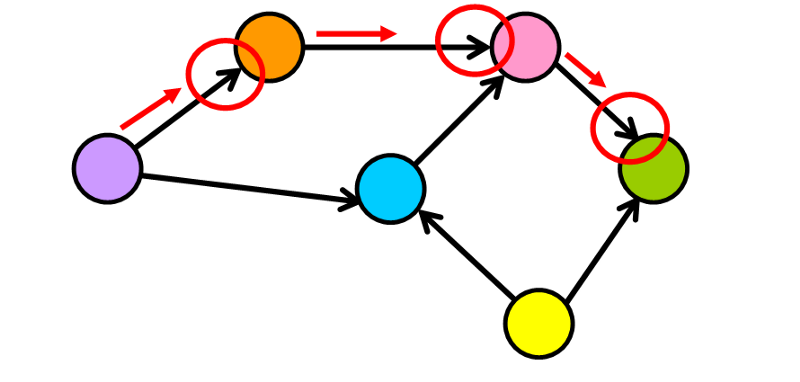
2️⃣ Undirected Graphs
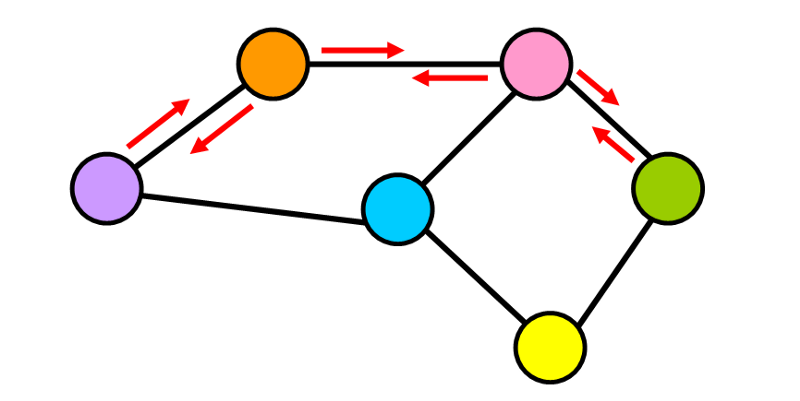
In this type of graph, edges are undirected (they do not have a specific direction). Think of undirected edges as two-way streets. You can go from one node to another and return through that same “path”.
💡 Note: When you see a diagram of a graph where the edges don’t have arrows pointing in a specific direction, you can assume that the graph is undirected.
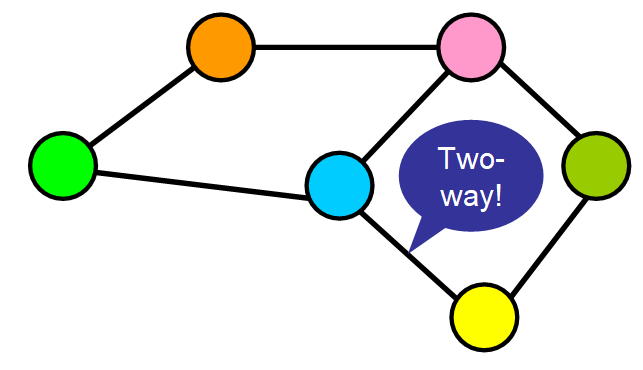
🍕 For our pizza delivery service, this would mean that the delivery motorcycle can go from the source to the destination through the same street or path (To their relief! 😇).
In the graph below, you could go from the purple node to the green node and back through the same path, so you don’t reach a point no return. 😌
🏋 Weights? — Yes, Weights!
1️⃣ Weighted Graphs
In weighted graphs, each edge has a value associated with it (called weight). This value is used to represent a certain quantifiable relationship between the nodes they connect.
For example, weights could represent distance, time, the number of connections shared between two users in a social network, or anything that could be used to describe the connection between nodes in the context that you are working with.
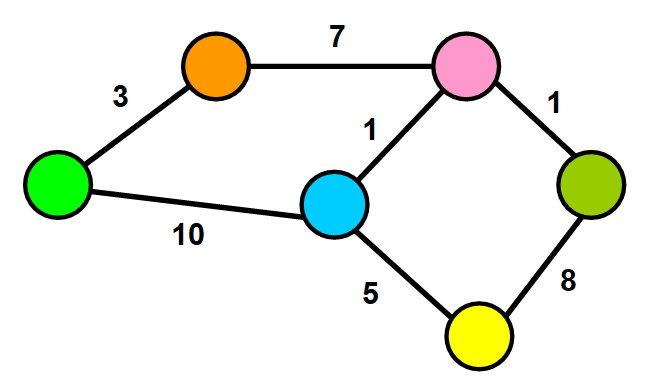
These weights are used by Dijkstra’s Algorithm to optimize routes by finding the shortest or least expensive paths between nodes in a network. (Stay tuned for an article on Dijkstra’s Algorithm! 😃).
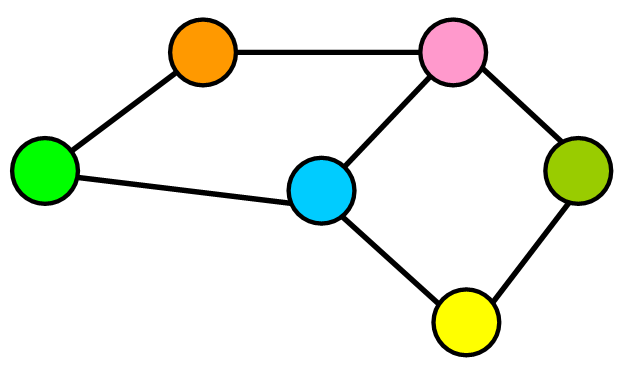
2️⃣ Unweighted Graphs
In contrast, unweighted graphs do not have weights associated with their edges. An example of this type of graph can be found in social networks, where edges represent the connection between two users. The connection cannot be quantified. Therefore, the edge has no weight.
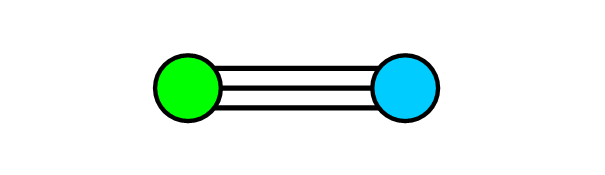
💡 Note: You may have noticed that, so far, our graphs only have one edge connecting each pair of nodes. It’s natural to ask if there could be more than one edge between a pair of nodes. Actually, this is possible with Multigraphs! They can have multiple edges connecting the same pair of nodes.
🏆 Number of Edges! — An Important Factor
It’s very important to know if a graph has many or few edges because this is a crucial factor to decide how you will represent this data structure in your code. Let’s see the different types! 👍
1️⃣ Dense Graphs
Dense graphs have many edges. But, wait! ⚠️ I know what you must be thinking, how can you determine what qualifies as “many edges”? This is a little bit too subjective, right? 😇 I agree with you, so let’s quantify it a little bit:
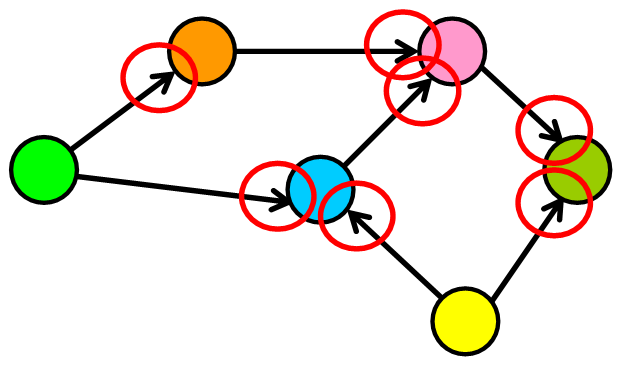
👉 Let’s find the maximum number of edges in a directed graph. If there are |V| nodes in a directed graph (in the example below, six nodes), that means that each node can have up to |v| connections (in the example below, six connections).
Why? Because each node could potentially connect with all other nodes and with itself (see “loop” below). Therefore, the maximum number of edges that the graph can have is |V|*|V| , which is the total number of nodes multiplied by the maximum number of connections that each node can have.
When the number of edges in the graph is close to the maximum number of edges, the graph is dense. 😉
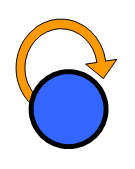
💡 Note: “Loops” occur when a node has an edge that connects it to itself. Strange and interesting, right? 😄
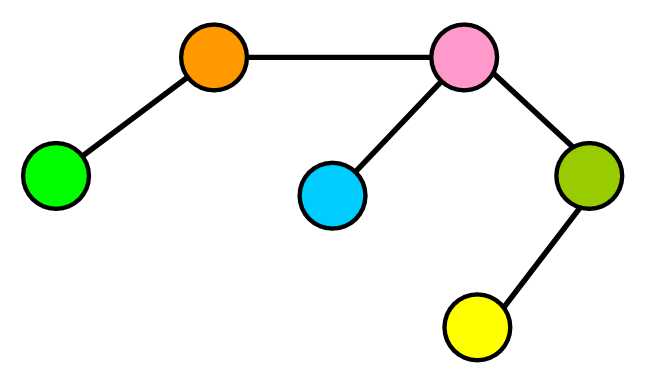
2️⃣ Sparse Graphs
Sparse Graphs have few edges. As you can see in the diagram below, there aren’t many connections between the nodes.
When the number of edges in the graph is significantly fewer than the maximum number of edges, the graph is sparse. 😉
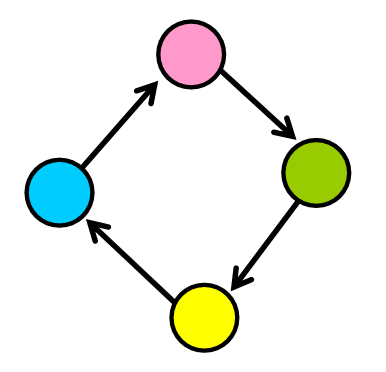
⭕️ Meet Cycles!
Now let’s see a vital concept to understand graphs, cycles.
You probably noticed that if you follow a sequence of connections in a graph, you may find a path that will take you back to the same node. This is like “walking in circles”, exactly as if you were driving around your city and you took a path that could take you back to your initial location.
In graphs, these “circular” paths are called “cycles”. They are valid paths that start and end at the same node. For example, in the diagram below, you can see that if you start at any node, you can return to that same node by following the edges.
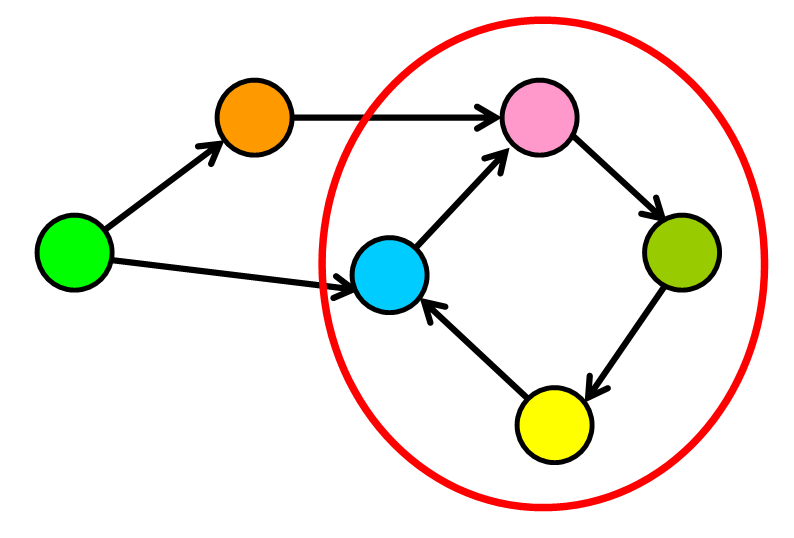
Cycles are not always “isolated” because they can be part of a larger graph. You can detect them by starting your search on a specific node and finding a path that takes you back to that same node.
👋 In Summary…
- Graphs are awesome data structures that you use every day through Google Search, Google Maps, GPS, and social media.
- They are used to represent elements that share connections.
- The elements in the graph are called Nodes and the connections between them are called Edges.
- Graphs can be directed, when their edges have a specific orientation, similar to one-way streets, or undirected, when their edges don’t have a specific orientation, similar to two-way streets.
- Edges can have a value associated with them, called weight.
- If a graph has many edges, it’s called a dense graph. Otherwise, if it has few edges, it’s called a sparse graph.
- A series of connections can form a cycle if they create a path that lets you to return to the same node.
Continue learning about these amazing data structures! It will be totally worth it for your future as a developer. I’m learning about data structures right now, and I find them completely fascinating. 😃 🎆 ❤️
The important thing is to not stop questioning. Curiosity has its own reason for existing. — Albert Einstein
👋 Thank you!
I really hope that you liked my article. ❤️
Follow me on Twitter. 😃