Computers perform complex calculations when carrying out their assigned tasks. At the very core, the calculations boil down to operations like comparisons, assignments, and addition.
Have you ever wondered how they are performed under the hood and why they are important? At a fundamental level, a computer works by performing various numerical conversions.
In this article, you'll learn the following concepts:
The importance of numerical systems in computers.
Types of numerical systems.
Numerical conversion techniques.
Application of different numerical systems.
Mini exercises to keep you engaged along the way.
Types of Numerical Systems
Numerical conversion is the process of converting numbers from one numeral system to another. In computer systems, the common numeral systems include decimal (base-10), binary (base-2), hexadecimal (base-16), and octal (base-8).
But What Is a Base?
In mathematics and computer science, the term "base" refers to the number of unique digits or symbols used in a positional numeral system. Each digit's value is multiplied by the base raised to the power of its position in the number, starting from the rightmost digit, which represents the units place.
Here's an explanation of the commonly encountered numeral systems:
Base-2 (Binary):
Base-2, or binary, uses only two symbols: 0 and 1.
Each digit's value is a power of 2, with positions increasing from right to left.
Base-10 (Decimal):
Base-10, or decimal uses ten symbols from 0 to 9.
Each digit's value is a power of 10, with positions increasing from right to left.
Base-8 (Octal):
Base-8, or octal, uses eight symbols: 0 to 7.
Each digit's value is a power of 8, with positions increasing from right to left.
Base-16 (Hexadecimal):
Base-16, or hexadecimal, uses sixteen symbols: 0 to 9 and A to F (representing 10 to 15).
Each digit's value is a power of 16, with positions increasing from right to left.
Below is a table showing the mapping of hexadecimal numbers from 10 with alphabets.
| Character | Hexadecimal |
| A | 10 |
| B | 11 |
| C | 12 |
| D | 13 |
| E | 14 |
| F | 15 |
This notation is commonly used to simplify the representation of binary-coded values.
Importance of Understanding Numerical Systems in Computers
Learning numeral conversions in computer science is essential for several reasons:
Understanding Data Representation: Computers store and manipulate data using binary (base-2) representation. Knowing how to convert between numeral systems helps in understanding how data is stored and processed at the fundamental level.
Addressing Memory: Memory addresses in computers are frequently represented in hexadecimal format. Knowing how to convert between decimal and hexadecimal is crucial for understanding memory management and for debugging.
Networking and Communication: In networking, IP addresses and MAC addresses are often represented in hexadecimal format. Understanding hexadecimal conversion is thus comes in handy for networking professionals.
Cryptography: In cryptography, hexadecimal numbers are frequently used to represent keys, cipher texts, and other cryptographic data. Understanding numeral conversions helps in understanding cryptographic operations.
Conversion Techniques
In this section, you'll learn techniques to convert one number system to another.
Decimal to Binary
Step-by-Step Conversion Process:
Divide the number by 2: The first step is to divide the number by 2 and record the remainder.
Divide the quotient by 2 repetitively: Divide the quotient from step 1 and record the remainder. Continue to divide and record the remainder till 1 remains as the quotient.
Find the solution in reverse order: Starting from the last quotient that would be
1, go upwards to get the final answer.
Example Conversion:
Let's say you want the binary equivalent of 17, then the process would be like this:
| Operation | Result | Remainder |
| 17/2 | 8 | 1 ⬆️ |
| 8/2 | 4 | 0 ⬆️ |
| 4/2 | 2 | 0 ⬆️ |
| 2/2 | 1 ➡️ | 0 ⬆️ |
To find the final answer, follow the arrows. Start from the bottom where the result is 1 and go upwards. You'll get 10001.
So,
$$17_{10} = 10001_{2}$$
Let's try a bigger number 55
| Operation | Result | Remainder |
| 55/2 | 27 | 1 ⬆️ |
| 27/2 | 13 | 1 ⬆️ |
| 13/2 | 6 | 1 ⬆️ |
| 6/2 | 3 | 0 ⬆️ |
| 3/2 | 1 ➡️ | 1 ⬆️ |
So,
$$55_{10} = 110111_{2}$$
Now, your turn:
What is 67 in binary?
Show Answer
67 in binary is 1000011.Binary to Decimal
Step-by-Step Conversion Process:
Write down the binary number: Separate each bit for clarity.
Map each bit with its corresponding power of 2: Start from
2^0on the right and increase the exponent by1as you move left.Multiply each bit by its corresponding power of 2: If the bit is 1, multiply it by the power of 2 for that position. If the bit is 0, the result is 0 for that position.
Sum all the products: Add all the results from step 3 to get the decimal equivalent.
Example Conversion:
For 101, the conversion would be like this:
$$\begin{align} &1\times2^2 + 0\times2^1 + 1\times2^0 \newline &= 4 + 0 + 1 \newline &= 5 \end{align}$$
So,
$$101_{2} = 5_{10}$$
Let's convert 1011001 to decimal:
$$\begin{align} &1\times2^6+0\times2^5+1\times2^4+1\times2^3+0\times2^2+0\times2^1+1\times2^0\newline &= 64+0+16+8+0+0+1 \newline &= 89 \end{align}$$
So,
$$1011001_{2} = 89_{10}$$
Binary to Hexadecimal
Step-by-Step Conversion Process:
Make pairs of 4: Segregate the given binary number into 4 bits each, starting from the rightmost bit.
Pad in 0 to the left-most pair if the bits do not count to 4: If the leftmost part doesn't make 4 bits, add zeros to the left of it to complete the count.
Find equivalent decimal number as explained previously: Use binary to decimal conversion.
Example Conversion:
Let's convert 10010010 to hexadecimal.
Split the bits into sections of 4 bits each, starting from the rightmost bit:
10010010= [1001][0010]Padding was not needed here as each section is 4 bits long.
Convert binary to decimal:
$$\begin{align} &[1001][0010]\newline &=[1\times2^3 + 0\times2^2 + 0\times2^1 + 1\times2^0] [0\times2^3 + 0\times2^2 + 1\times2^1 + 1\times2^0] \newline &=[8+0+0+1][0+0+1+1] = [9][2] \end{align}$$
So,
$$10010010_{2} = 92_{16}$$
Let's run another example. But first,
Recall that, the numbers 10 - 15 are represented as follows in hexadecimal:
| Character | Hexadecimal |
| A | 10 |
| B | 11 |
| C | 12 |
| D | 13 |
| E | 14 |
| F | 15 |
Let's convert 11010011011 to hexadecimal.
Divide the bits into groups of 4, starting from the right.
- [110][1001][1011]
Add padding of
0to the leftmost section.- [0110][1001][1011]
Convert the bits to decimal using the binary-to-decimal method.
$$\begin{align} &[0110][1001][1011]\newline &=[0\times2^3+1\times2^2+1\times2^1+0\times2^0]\ [1\times2^3+0\times2^2+0\times2^1+1\times2^0]\ [1\times2^3+0\times2^2+1\times2^1+1\times2^0]\newline &=[6][9][11]\newline &=[6][9][B] \end{align}$$
As
11maps toBin hexadecimal, replace11withB.$$[6][9][11] =[6][9][B]$$
So,
$$11010011011_{2} = 69B_{16}$$
Hexadecimal to Binary
Step-by-Step Conversion Process:
Example Conversion:
Identify Each Hexadecimal Digit: Break down the hexadecimal number into individual digits.
Convert Each Hexadecimal Digit to Binary: Each hexadecimal digit corresponds to a unique four-bit binary sequence.
Example Conversion:
Let's convert the hexadecimal number 2F3 to binary.
Identify Each Hexadecimal Digit:
2F3
Convert Each Hexadecimal Digit to Binary:
2in binary:0010Fis15in decimal and in binary:11113in binary:0011
Combine the Binary Sequences:
2F3in binary:0010 1111 0011
So, the hexadecimal number 2F3 converts to 001011110011 in binary.
Octal to Binary
Step-by-Step Conversion Process:
Example Conversion:
To convert an octal number to binary, each octal digit (0-7) is converted to a three-bit binary number because the largest octal digit (7) can be represented using three bits (111).
Step-by-Step Conversion Process:
Identify Each Octal Digit: Break down the octal number into individual digits.
Convert Each Octal Digit to Binary: Use the same decimal-to-binary conversion method.
Combine the Binary Sequences: Each sequence should be 3 bits, pad zeros to the left if needed. Concatenate the three-bit binary sequences to form the final binary number.
Example Conversion:
Let's convert the octal number 157 to binary.
Identify Each Octal Digit:
157
Convert Each Octal Digit to Binary:
1in binary:0015in binary:1017in binary:111
Combine the Binary Sequences:
157in binary:001 101 111
So, the octal number 157 converts to 001101111 in binary.
Binary to Octal
To convert a binary number to an octal, group the binary digits into sets of three, starting from the right to the left. You can pad that group with leading zeros if the left-most group isn't 3 digits.
Step-by-Step Conversion Process:
Pad the Binary Number with Leading Zeros (if necessary) to make the number of digits in groups of three:
Binary:
11010011Padded Binary:
011 010 011
Group the Binary Digits into Sets of Three:
- Groups:
011 010 011
- Groups:
Convert Each Group of Three Binary Digits to Its Octal Equivalent:
- Use the same method as binary to decimal.
Combine the Octal Digits: Form the final octal number by combining the octal digits.
Example Conversion:
Let's convert the binary number 11010011 to octal.
Pad the Binary Number with Leading Zeros (if necessary):
Binary:
11010011Padded Binary:
011 010 011
Group the Binary Digits into Sets of Three:
- Groups:
011 010 011
- Groups:
Convert Each Group of Three Binary Digits to Its Octal Equivalent:
011(binary) =3(octal)010(binary) =2(octal)011(binary) =3(octal)
Combine the Octal Digits:
11010011in octal:323
So, the binary number 11010011 converts to 323 in octal.
Applications of Numerical Conversions
In this section, you'll learn about two common applications of numerical conversions.
File permissions
Octal notation is commonly used in file permission management in Unix-like operating systems. In Unix systems, each file has associated permissions that determine who can read, write, or execute the file. These permissions are represented by a 3-digit octal number, where each digit corresponds to a specific set of permissions: owner, group, and others.
Each digit in the octal representation is composed of three bits, with each bit representing a specific permission:
The first digit represents permissions for the file owner.
The second digit represents permissions for the group associated with the file.
The third digit represents permissions for others (users not in the owner group).
The mapping of permissions to bits is as follows:
Read permission corresponds to the value
4.Write permission corresponds to the value
2.Execute permission corresponds to the value
1.
To calculate the octal representation of permissions, you sum the values of the granted permissions. For example:
- If a file has read and write permissions for the owner, read-only permissions for the group, and no permissions for others, the octal representation would be
640.
Here's the breakdown:
| Permission | Owner | Group | Others |
| Read = 4 | Yes | Yes | No |
| Write = 2 | Yes | No | No |
| Execute = 1 | No | No | No |
| 4 +2 + 0 = 6 | 4 +0 + 0 = 4 | 0 |
The owner has read (4) + write (2) permissions, resulting in 6.
The group has read (4) permissions only.
Others have no permissions, which corresponds to 0.
So, the permissions for the file in octal representation are 640.
Quiz:
What does the permission 777 show?
This octal representation of permissions provides a concise and efficient way to manage file permissions in Unix systems, allowing for easy understanding and manipulation of access rights.
To learn more about file permissions, you can read my other article here.
Color codes
You might have noticed that the notation #ffffff, #c3c400 are prevalent in various digital contexts, such as web design, graphics editing software, and programming. As you might have guessed, this is a hexadecimal representation. As an example, see this palette from Colorhunt:
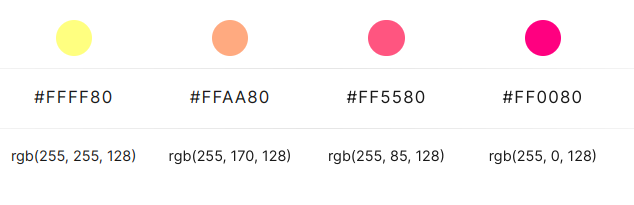
Here we have a hexadecimal value of the color followed by the equivalent RGB value.
Hexadecimal color codes represent colors in the RGB model using pairs of hexadecimal digits for each color component (red, green, and blue). Each pair corresponds to an 8-bit value, ranging from 00 to FF, where 00 represents the lowest intensity(black) and FF represents the highest intensity(white).
For instance, #FF0000 stands for red, #00FF00 stands for green, and #0000FF stands for blue.
QUIZ:
If red and green makes yellow in RGB model, what would be the hex equivalent?
Conclusion
By the end of this article, you should be comfortable with carrying out most of the common conversions. In this article, you:
Explored the importance of numerical conversions in computers.
Explored numeral systems like binary, decimal, hexadecimal, and octal.
Learned conversion techniques between these systems.
Understood some practical applications of numeral systems in computing.
Next steps
You can code a decimal to binary converter in JavaScript by following this step-by-step guide.
I hope you found this article helpful. I would love to connect with you on any of these platforms.
See you in the next tutorial, happy coding 😁

