Data structures and algorithms are the heart and soul of computer science and software. One cannot learn programming without understanding how data is organized in code and how to manipulate it.
One such data structure is a binary tree:

Oh no not that kind of tree, I mean this one:
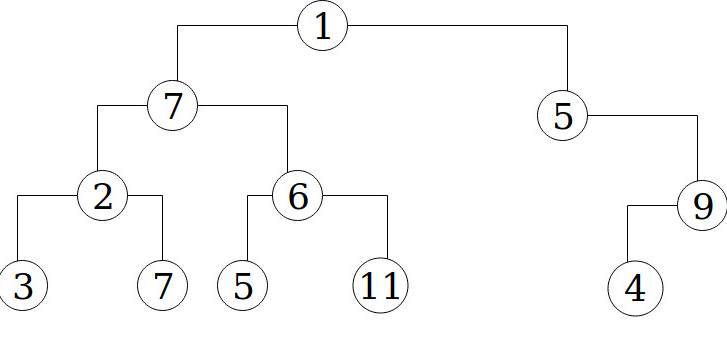
In simple terms, a tree is network of ‘nodes’. A node is an object whose properties include the data itself and pointers to its ‘children’. For a binary tree, the maximum number of children each node can have is 2. A binary tree will have a root node and at most two children. Each child is just a pointer to another tree object or it can be nil. Using a hash, this can be visualized as:
tree = {
:data => 1,
:left_child => [another_tree] || nil,
:right_child => [another_tree_again] || nil
}Before we go into height computations let us first find some uses for binary trees.
If you observe the directories or file structure in your computer, it follows a (albeit the more general) tree structure. Each folder can contain files (the data) and a number of other directories (which are not necessarily data in themselves but rather just addresses of such data contained within those sub directories). There are other use cases for binary trees that discussed better by other articles:
Binary trees are a vast subject and there are so many things that I can write about them (such as the different ways to search through them — a future article perhaps?). However, here I will be very specific — computing the height of a binary tree.
The first thing to understand in relation to this, is that we can represent a binary tree using an array. But even though that’s possible, there are a number of ways to lay down each node and associate them (as an element in an array) to their respective left and right children.
For simplicity we’ll use the “breadth-first” method of flattening the tree. In ‘breadth-first’ we place the data contained in each node starting from the root. Then we go to the next lower level, laying down each node’s data from left to right. We go through all the levels until the lowest one.
If a sub tree has no left or right child then such child can be represented as 0, as long as the sub tree isn’t in the lowest level in the binary tree.
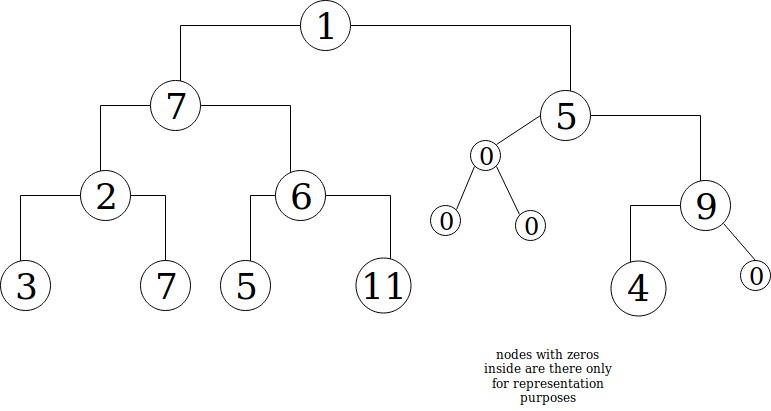
tree = [1, 7, 5, 2, 6, 0, 9, 3, 7, 5, 11, 0, 0, 4, 0] (T0)* array representation of Figure2Numerically, we can compute the positions of the left and right children of each node:
left child of tree[i] is at index 2*i + 1 (T1)right child of tree[i] is at index 2*i + 2 (T2)As we can see from figure 2 we can tell how tall a tree is — that is we just need to count how many nodes there are from the root down to the lowest element (including the root and the lowest element) along the longest branch. But when it’s already in array form, how do we know how tall it is?
First we must have a general formula for the height of any tree:
height = 1 + max of(left_child_height, right_child_height) (T3)For multilevel trees then we can conclude that in order to compute the height of any sub-tree (and the tree itself) we first must compute the heights of the left and right children and then find the higher between the two. In computing the heights of these two children we need to compute the heights of their respective children and so on.
Having this we can now begin to outline an algorithm for computing the height of multilevel binary trees. There are two methods we can take, one is using iterations or loops, and the other, because of the repetitive nature of the steps (previous paragraph), is using recursion. I will follow up this article with a discussion on how to use recursion to do this. However, that would be too easy. So let’s learn the hard way first: we’ll do this using iteration.
Iterative Method
We will use the tree array T0 above to illustrate this process
Step 0: Declare a heights array which will store the heights of each sub tree.
heights = [] (S0.1)Step 1: Iterate through the array — since we need to compute the heights of the descendants first, we iterate from the last element. And instead of using each method directly in the tree array we will use it for the indices of each element.
(tree.length - 1).downto(0) do |i| (S1.1)Step 2: For each element, find initial height — if the element is zero (meaning it’s actually a nil node) then initial height is 0, else it is 1.
initial_height = tree[i] == 0 ? 0 : 1 (S2.1)Step 3: Find height of left child — inside heights array, if the element has a left child then the height of this child is equal to:
left_child_height = heights[left_child_index] (S3.1)In the above, the left_child_index can be computed as follows:
left_child_index = heights.length - i - 1 (S3.2)I came up with S3.2 through a little trial and error. In the simulation that will follow these series of steps I will make mention of it.
To summarize though, I initially intended to unshift each descendant’s heights into heights so that the heights of each element would have the same indices as the element itself has on trees. But as I’ll later note, using unshift for this will be taxing resource wise for large array inputs.
So then I decided to use push. Each height will then be ordered in reverse compared to their corresponding elements’ order in tree. So that the height, let’s say of tree[0] will ultimately be located in heights[-1].
If the element in question has no left child then left_child_index should be nil. To ensure that we catch this scenario:
left_child_index = nil if tree[2*i + 1].nil? (S3.3)Putting S3.2 and S3.3 together using a ternary:
left_child_index = tree[2*i + 1].nil? ? nil : heights.length - i -1 (S3.4)Therefore, the height of the left child will have to be 0 if left child is nil. The full formula for left_child_height then is:
left_child_height = left_child_index.nil? ? 0 : heights[left_child_index] (S3.5)Step 4: Find height of right child — finding the height of the right child of a sub tree follows the same logic as Step 3. Since we are filling up heights array from left to right (using push) and we are iterating tree from right to left, the height of the right child of any sub tree will always be pushed first to heights. Therefore, the left child of any element will be at position left_child_index -1 inside heights (if right child is not nil in tree). Taking these into consideration and following the logic of Step 3:
right_child_index = tree[2*i + 2].nil? nil : left_child_index - 1 (S4.1)right_child_height = right_child_index.nil? ? 0 : heights[right_child_index] (S4.2)Step 5: Find element’s total height — After finding the heights of the left and right children of the element in question (at i index in Ltree), we can now find that element’s total height:
total_height = initial_height + [left_child_height, right_child_height].max (S5.1)Numerically speaking, if the element is 0 and it happens to have any child(ren) inside tree then such child(ren) will also be 0. Hence, its total_height will also be 0. Such is the case with element at i = 5 in T0 above:
left right
child child
tree = [1, 7, 5, 2, 6, 0, 9, 3, 7, 5, 11, 0, 0, 4, 0]
i=5 i=11 i=12
element in question
(T0 here repeated)
total_height = 0 + [0,0].max = 0 (S5.2)But for the element at i = 4, the height is:
left right
child child
tree = [1, 7, 5, 2, 6, 0, 9, 3, 7, 5, 11, 0, 0, 4, 0]
i=4 i=9 i=10
element
in question
total_height = 1 + [1,1].max = 2 (S5.3)In S5.3 and S5.4 above we just used visual inspection to compute the heights of the right and left children of the element in question. But this illustrates how our algorithm works. Now after computing for the total_height we simply:
Step 6: Push total_height into heights — As I noted before, using the push method is more efficient, especially for large arrays.
heights.push(total_height) (S6.1)Once we have iterated through all elements in the tree array, we will have an array heights composed of the heights of each sub tree in the binary tree. It should look like this:
heights(after full iteration) = [0, 1, 0, 0, 1, 1, 1, 1, 2, 0, 2, 2, 3, 3, 4] (S6.2)Step 7: Return height of the binary tree — If our goal is just find out the height of the mother tree (meaning from the root down to the lowest-rightmost node) then we simply:
return heights[-1] (S7.1)
*Note if this is the last line in the method then the 'return' keyword is redundant (in Ruby at least)However, a lot of times we may be interested to compute for the heights of any of the sub trees. In that case we simply return the heights array itself and then anyone using the program can simply include any index to find the height of a specific branch in the tree.
The full method below:
def binary_tree_height(tree_array)
#0 Declare a heights array which will store the heights of each sub tree
heights = []
#1 Iterate through the tree_array starting from last element down to first
(tree_array.length - 1).downto(0) do |i|
#2 For each element, find initial height
initial_height = tree_array[i] == 0 ? 0 : 1
# 3 Find height of left child
left_child_index = tree_array[2*i + 1].nil? ? nil : heights.length - i - 1 #index of left child's height in heights
left_child_height = left_child_index.nil? ? 0 : heights[left_child_index]
# 4 Find height of right child
right_child_index = tree_array[2*i + 2].nil? ? nil : left_child_index - 1 #index of right child's height in heights
right_child_height = right_child_index.nil? ? 0 : heights[right_child_index]
# 5 Find element's total height
total_height = initial_height + [left_child_height,right_child_height].max
# 6 Push total height to heights array
heights.push(total_height)
end
puts heights[-1]
end
Let’s test this algorithm out.
Let us suppose we run binary_tree_height(tree). Computing for the heights of tree[14] down to tree[7] is pretty straightforward (they will either be 0 or 1 since they are all at the lowest level of tree) so we won’t simulate them anymore here. We will assume we are already in that part of the iteration when i will be equal to 6. Therefore, at this juncture:
i = 6 (F1)
tree[6] = 9 (F2)
heights = [0, 1, 0, 0, 1, 1, 1, 1] (heights.length at this point is 8) (F3)Now, we can see that tree[6] is equal to 9 (and not 0). Therefore:
initial_height = 1 (F4)As promised, here is how I came up with the formula for the indices of the left and right children.
So I began with a heights array already filled with the heights of the lowest elements as shown in F3. Since I’m now working with tree[6] (which is 9) then its left and right children are tree[13] and tree[14]; whose corresponding heights are in heights[1] and heights[0], respectively. If that’s not clear enough, we know we push starting from tree[14] — this will become heights[0]. We then compute for and push the height of tree[13] — this will be heights[1]. Relating the indices:
index of left child in trees = 13
index of left child's height in heights = LEFT_INDEX =1
index of right child in trees = 14
index of right child's height in heights = RIGHT_INDEX = 0
current index of element in question = MOTHER_INDEX = 6
current length of heights array = LENGTH = 8
LEFT_INDEX = 1 = 8 - 6 - 1 = LENGTH - MOTHER_INDEX - 1
RIGHT_INDEX = 0 = 8 - 6 - 2 = LENGTH - MOTHER_INDEX - 2
(or simply LEFT_INDEX -1 ) (F5)We can now apply this logic to all elements, so then in code we compute for the height of tree[6] as follows:
Computing for tree[6]'s left child's height:
from code at S3.4:
left_child_index = tree[2*i + 1].nil? ? nil : heights.length - i - 1
Since tree[2*6 + 1] = tree[13] = 4 is not nil then:
left_child_index = 8 - 6 - 1 = 1
from code at S3.5:
left_child_height = left_child_index.nil? ? 0 : heights[left_child_index]
So then:
left_child_height = heights[1] = 1Following the same for tree[6]’s right child’s height:
from code at S4.1:
right_child_index = tree[2*i + 2].nil? nil : left_child_index - 1
Since tree[2*6 + 2] = tree[14] = 4 and is not nil:
right_child_index = left_child_index -1 = 1 -1 = 0 -> !nil?
and from code at S4.2:
right_child_height = right_child_index.nil? ? 0 : heights[right_child_index]
Therefore: right_child_height = heights[0] = 0Now we can find the total height of tree[6]:
total_height (tree[6]) = 1 + [1,0].max = 1 + 1 = 2We can then push this total_height into heights:
heights.push(2), such that:heights = [0, 1, 0, 0, 1, 1, 1, 1, 2]And the same thing goes on until we work on tree[0] and the final heights array should be:
heights = [0, 1, 0, 0, 1, 1, 1, 1, 2, 0, 2, 2, 3, 3, 4]And returning heights[-1] (or heights[heights.length -1], whichever we prefer), we determine that the height of tree is 4. We can verify this visually in both figures 1 and 2 above.
It took us 7 steps to come up with the answer. With this size of tree array the operation took around 0.024 milliseconds to finish. It takes half the time (only 0.012 milliseconds) for the same thing to be accomplished using recursion.
As a preview on how to do this recursively, we can simply do something like:
def tree_height_recursive(tree_array, index = 0)
return 0 if tree_array[index].nil? or tree_array[index] == 0
left_child_height = recursive_tree_height(tree_array, 2*index + 1)
right_child_height = recursive_tree_height(tree_array, 2*index +2)
total_height = 1 + [left_child_height, right_child_height].max
endWe see that recursion probably will only take us at most 4 steps to do the same task. And it saves us half of the time and less resources used.
One secret for learning algorithms is hard work and practice. It also helps if you work collaboratively with others. I actually did the above not alone but with my coding partner. I previously wrote about how learning this way is so much more productive and effective.
Here is my repository on the different data structures and algorithms that I’ve worked on.

