How to Use JavaScript's Map() Method to Solve Breadth-First and Depth-First Search Problems

The JavaScript map() method is an object with a key and value pair. An object's key and value are connected using a colon (:) while the key and value of a map are connected using an arrow (=>).

Here's an example of an object in JavaScript:

{ a: [ 1, 2, 3 ], b: 2, c: 3 }

A JavaScript Object

And here's an example of a map in JavaScript:

{ 'a' => [ 1, 2, 3 ], 'b' => 2, 'c' => 3 }

A JavaScript Map

The map() method is a good tool for solving algorithm and data structure problems like graphs, shortest distance, and best route. Many transport companies have used this method to build their application. We will be doing something like that in this tutorial.

I have added videos at the end of various sections of this tutorial for those who may prefer visual tutorials.

Goal of This Article

This tutorial aims to teach you how the map() method works and how you can use it when solving Breath-First search and Depth-First search problems.

By the end, you will have learned the basics of the map() method, and you will have seen another perspective on solving algorithm and data structure problems such as graphs, Breadth-First search (BFS), and Depth-First search (DFS).

Prerequisites

This tutorial assumes that you have already worked with basic Javascript concepts such as strings, arrays, objects, and sets. It may also be helpful to read up about algorithms and data structures.

Let's hit the road!

The Problem

Nigeria has 36 states. A tourist can move from one state to another by road, air, and water bodies known as routes. What we want to do is to programmatically:

Show each state and the other states connected to it in a graph.
Check if you can connect two (2) states.

So we are given eleven (11) out of Nigeria's thirty-six (36) states to work with:

ENUGU, ABIA, SOKOTO, NIGER, LAGOS, OGUN, BAYELSA, AKWAIBOM, ANAMBRA, IMO, EBONYI

These are the routes:

ENUGU to LAGOS
ENUGU to NIGER
NIGER to SOKOTO
NIGER to ANAMBRA
SOKOTO to ANAMBRA
OGUN to LAGOS
OGUN to ABIA
OGUN to EBONYI
OGUN to BAYELSA
EBONYI to ABIA

Let's use these data to solve the problem!

How to Solve the Problem

In the previous section, we saw the problem. Now we'll solve that problem here. I will use Replit for this tutorial.

Replit gives you a well-equipped IDE to quickly write and test programs like the one we are about to write.

How to Set Up the Map

The first problem we want to solve is to programmatically show each state and the other states connected to it.

Start by defining the eleven (11) states and their routes. Enter the following code:


const states = 'ENUGU ABIA SOKOTO NIGER LAGOS OGUN BAYELSA AKWAIBOM ANAMBRA IMO EBONYI'.split(' ');

const routes = [
  ['ENUGU', 'LAGOS'],
  ['ENUGU', 'NIGER'],
  ['NIGER', 'SOKOTO'],
  ['NIGER', 'ANAMBRA'],
  ['SOKOTO', 'ANAMBRA'],
  ['OGUN', 'LAGOS'],
  ['OGUN', 'ABIA'],
  ['OGUN', 'EBONYI'],
  ['OGUN', 'BAYELSA'],
  ['EBONYI', 'ABIA'],
];

Create a new map() or graph named connections:

const connections = new map();

Next, type the following code:

states.forEach((state) => {
  connections.set(state, []);
});

This code loops through all the states. It takes each state and sets it as a key in the connections graph with a default value of an empty array ([]).

If you log connections to the console, you will get the following result:

Map(11) {
  'ENUGU' => [],
  'ABIA' => [],
  'SOKOTO' => [],
  'NIGER' => [],
  'LAGOS' => [],
  'OGUN' => [],
  'BAYELSA' => [],
  'AKWAIBOM' => [],
  'ANAMBRA' => [],
  'IMO' => [],
  'EBONYI' => []
}

For now, picture the graph in the output above like in the image below:

Screenshot-2022-08-10-at-16.44.32 — Graphical Representation of The Given States

Enter the code below:

routes.forEach(route => {
  const departure = [...route][0];
  const destination = [...route][1];
  
  connections.get(departure).push(destination);
  connections.get(destination).push(departure);
});

This code adds states to the empty array values of the keys in the previous step. It circles through the routes array and extracts each route.

The departure state is set to the first item in the route array, while the destination state is the second.

It then adds the destination state to the array value of the departure state. Finally, the departure state gets included in the array value of the destination state.

At this point, if you log connections to the console, you will get the following result:

Map(11) {
  'ENUGU' => [ 'LAGOS', 'NIGER' ],
  'ABIA' => [ 'OGUN', 'EBONYI' ],
  'SOKOTO' => [ 'NIGER', 'ANAMBRA' ],
  'NIGER' => [ 'ENUGU', 'SOKOTO', 'ANAMBRA' ],
  'LAGOS' => [ 'ENUGU', 'OGUN' ],
  'OGUN' => [ 'LAGOS', 'ABIA', 'EBONYI', 'BAYELSA' ],
  'BAYELSA' => [ 'OGUN' ],
  'AKWAIBOM' => [],
  'ANAMBRA' => [ 'NIGER', 'SOKOTO' ],
  'IMO' => [],
  'EBONYI' => [ 'OGUN', 'ABIA' ]
}

This type of graph is undirected. An undirected graph is a type of graph where you can move from the node to the edge(s) and from the edge(s) back to the node. In our case, the node is the departure state, while the edge(s) is the destination state.

The following is a pictorial representation of the output above:

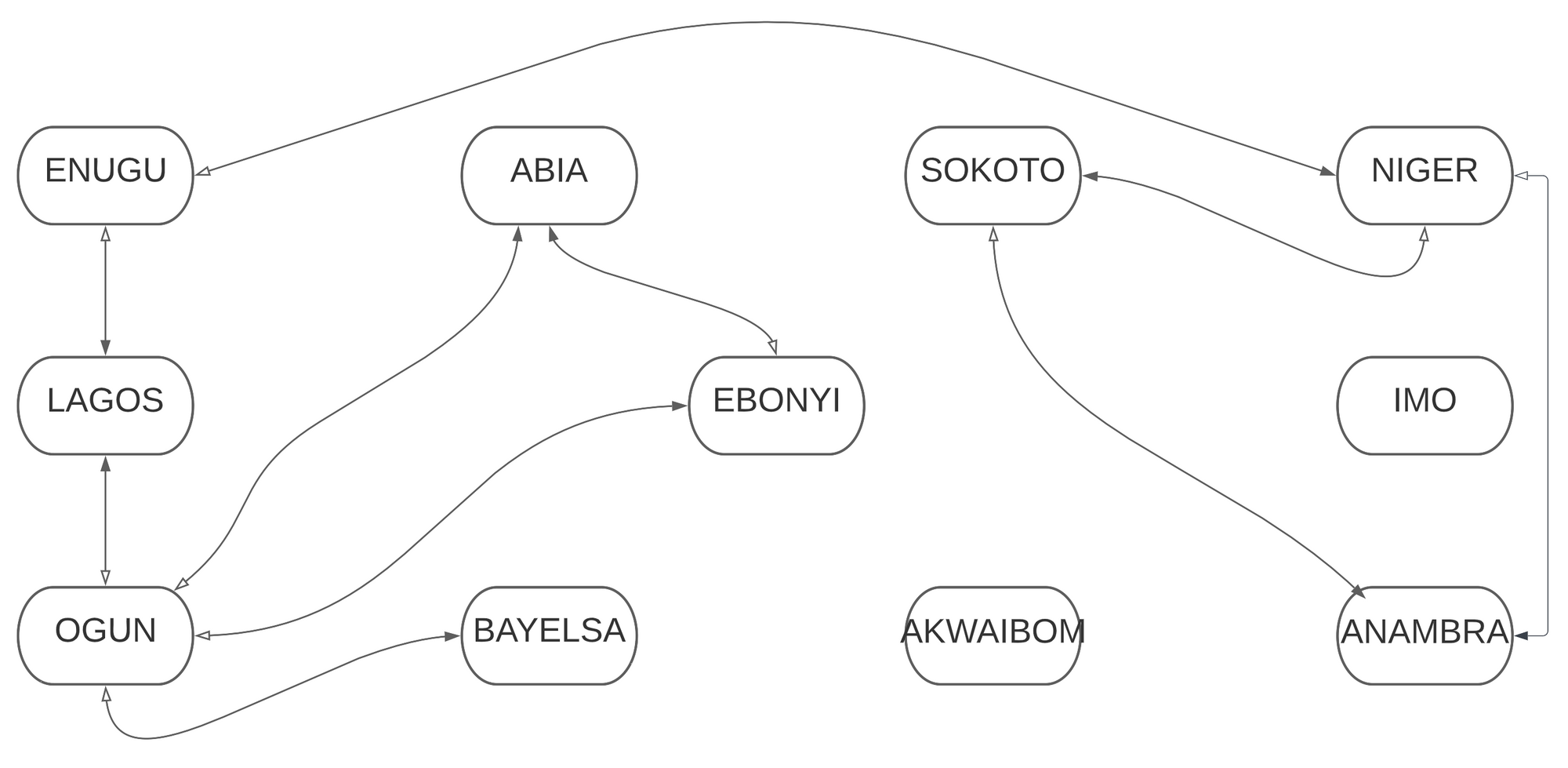
Screenshot-2022-08-10-at-16.29.30 — An Undirected Graph Representing The Routes

The arrowhead with a black color fill points to the destination state, while the arrowhead with a white color fill points to the departure state.

To make this graph directed, you can use this code instead:

routes.forEach(route => {
  connections.get([...route][0]).push([...route][1]);
});

Here is the output below:

Map(11) {
  'ENUGU' => [ 'LAGOS', 'NIGER' ],
  'ABIA' => [],
  'SOKOTO' => [ 'ANAMBRA' ],
  'NIGER' => [ 'SOKOTO', 'ANAMBRA' ],
  'LAGOS' => [],
  'OGUN' => [ 'LAGOS', 'ABIA', 'EBONYI', 'BAYELSA' ],
  'BAYELSA' => [],
  'AKWAIBOM' => [],
  'ANAMBRA' => [],
  'IMO' => [],
  'EBONYI' => [ 'ABIA' ]
}

The following is a pictorial representation of the output above:

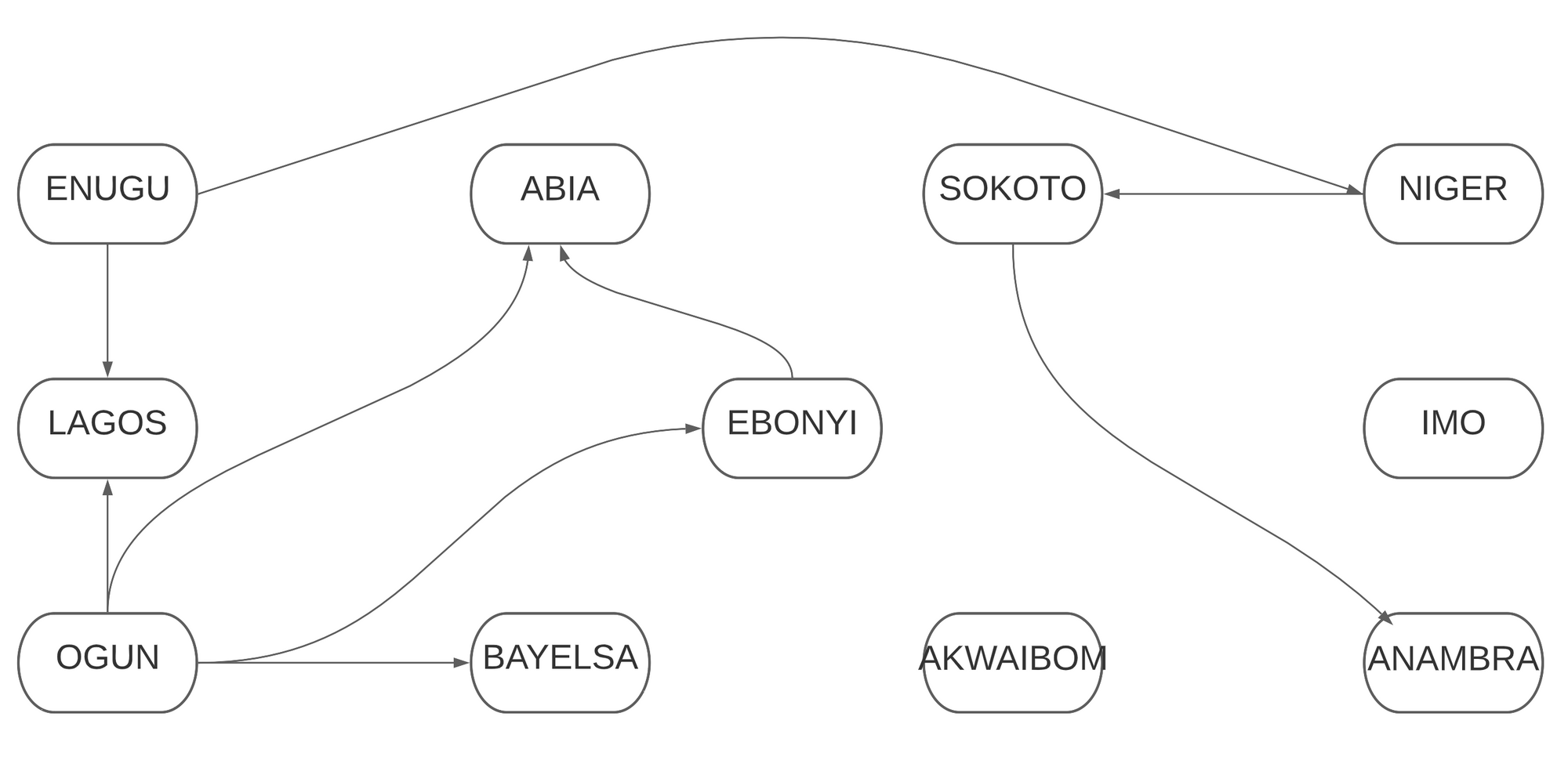
Screenshot-2022-08-10-at-16.06.57 — A Directed Graph Representing The Routes

If you find it difficult to understand, study the outputs and compare them with the given routes. The code will become easier as you practice.

We have been able to show how these states are connected programmatically. See what the code looks like so far:


const states = 'ENUGU ABIA SOKOTO NIGER LAGOS OGUN BAYELSA AKWAIBOM ANAMBRA IMO EBONYI'.split(' ');

const routes = [
  ['ENUGU', 'LAGOS'],
  ['ENUGU', 'NIGER'],
  ['NIGER', 'SOKOTO'],
  ['NIGER', 'ANAMBRA'],
  ['SOKOTO', 'ANAMBRA'],
  ['OGUN', 'LAGOS'],
  ['OGUN', 'ABIA'],
  ['OGUN', 'EBONYI'],
  ['OGUN', 'BAYELSA'],
  ['EBONYI', 'ABIA'],
];

const connections = new map();

states.forEach((state) => {
  connections.set(state, []);
});

console.log(connections)

routes.forEach(route => {
  const departure = [...route][0];
  const destination = [...route][1];
  
  connections.get(departure).push(destination);
  connections.get(destination).push(departure);
});

console.log(connections)

We are moving to the next part of the problem (to check if you can connect two (2) states.). We will do it in two (2) ways. First, we will explore the breadth-first search algorithm then we will do it using the depth-first search way.

How to Use Breadth-First Search

BFS is an algorithm used to inspect a tree or graph by exploring the direct children (edges) of a parent (node) before moving to the grandchildren. It continues in that manner till the end of the tree or graph.

For example, in our case, let's say we want to check if there is a possible connection between ENUGU and ABIA.

The BFS will start from Enugu and check all of Enugu's direct routes (LAGOS and NIGER). Since ABIA is not connected to ENUGU directly, the algorithm will move on to check the state(s) attached to LAGOS.

Next, the algorithm will inspect the state(s) linked to NIGER. The process will continue until it finds ABIA or meets a dead end. That terminates the program.

BFS uses a queue data structure. That means that items will be entered from one end and removed from the other end of an array. In our case, the queue will hold all states that have not yet visited. As we continue building the program, you will see it in action.

Let's start building the BFS by creating a function named bfs:

function bfs(departureState, destinationState) {

}

This function takes two (2) arguments, departureState, and destinationState.

Inside the function, define a queue and add the departureState in it:

  const queue = [departureState];

We are adding the departureState to the queue array since it holds all the nodes yet to be visited.

Next, define a new empty Set() named visited:

  const visited = new Set();

The visited variable will keep track of all the states visited just as the name indicates.

Now, we begin the search proper by navigating through the graph starting from the departureState. Enter the code below:

while (queue.length > 0) {
    
}

This loop will run as long as the queue is not empty. That means as long as there are still states not yet visited.

Remove the departureState from the queue before visiting it to prevent the code from running into an infinite loop. Use the code below:

    const state = queue.shift();

The code above removes each state from the front or top of the queue array since a queue employs the First-In-First-Out principle. An array inserts items from the back or bottom by default.

Retrieve the edges (destinations) connected to this node (state):

    const destinations = connections.get(state);

Now that we have access to the children (destinations) of the current node (state), let's check if any of them is the destinationState.

Loop through the destinations using this code:

for (const destination of destinations) {
    
}

At each point in this loop, check if the destination is the destinationState. If it is true, log a message to the console:

      if (destination === destinationState) {
          console.log("Found => " + destination);
      }

After that, add the destination to the visited and queue arrays if it is not in the visited already:

      if (!visited.has(destination)) {
        visited.add(destination);
        queue.push(destination);
      }

The program terminates when all states are in the visited array because there will be no state to add to the queue.

The bfs function now looks like this:

function bfs(departureState, destinationState) {
  const queue = [departureState];
  const visited = new Set();

  while (queue.length > 0) {
    const state = queue.shift();
    const destinations = connections.get(state);

    for (const destination of destinations) {
      if (destination === destinationState) {
          console.log("Found => " + destination);
      }

      if (!visited.has(destination)) {
        visited.add(destination);
        queue.push(destination);
      }
    }
  }
}

To check if there is a connection between two (2) states, say ENUGU and SOKOTO, call the bfs function like this:

bfs("ENUGU", "SOKOTO")

Below is the output:

Map(11) {
  'ENUGU' => [],
  'ABIA' => [],
  'SOKOTO' => [],
  'NIGER' => [],
  'LAGOS' => [],
  'OGUN' => [],
  'BAYELSA' => [],
  'AKWAIBOM' => [],
  'ANAMBRA' => [],
  'IMO' => [],
  'EBONYI' => []
}
Map(11) {
  'ENUGU' => [ 'LAGOS', 'NIGER' ],
  'ABIA' => [ 'OGUN', 'EBONYI' ],
  'SOKOTO' => [ 'NIGER', 'ANAMBRA' ],
  'NIGER' => [ 'ENUGU', 'SOKOTO', 'ANAMBRA' ],
  'LAGOS' => [ 'ENUGU', 'OGUN' ],
  'OGUN' => [ 'LAGOS', 'ABIA', 'EBONYI', 'BAYELSA' ],
  'BAYELSA' => [ 'OGUN' ],
  'AKWAIBOM' => [],
  'ANAMBRA' => [ 'NIGER', 'SOKOTO' ],
  'IMO' => [],
  'EBONYI' => [ 'OGUN', 'ABIA' ]
}
Found => SOKOTO
Found => SOKOTO

If what we have done so far is unclear, I suggest you break down the code at different points so that you can see how the program flows.

How to Use Depth-First Search

DFS algorithm takes one child of a node at a time. It continues searching down one child at a time of that node until it gets to a dead end before it backtracks and tries another child.

In our case, let's say we want to check if there is a possible connection between ENUGU and ABIA.

The DFS will start from Enugu and check the first state connected to it (LAGOS). Since LAGOS isn't ABIA, the search will examine the first state tied to LAGOS next. It will continue until it locates ABIA or meets a dead end. Then it will backtrack to check another node.

DFS uses a stack to keep track of the items (state(s) in our case) to be visited. When the stack becomes empty, the process ends. We'll use recursion in writing the code for the DFS algorithm. Let's get to it!

Begin by creating a function named dfs. It will take three (3) arguments (departureState, destinationState, and visited):


function dfs(departureState, destinationState, visited = new Set()) {
    
}

The visited array will hold the visited states to avoid an infinite loop. So the first thing to be done in the dfs function is to add the departureState into the visited array. Enter this code:

  visited.add(departureState);

Next, get the destinations of the departureState:

  const destinations = connections.get(departureState);

Now that we have the destinations of the departureState, we want to circle through them. Type the code below:

  for (let destination of destinations) {
      
  }

Inside the loop, check if the current destination is the destinationState. If it is true, display a message in the console. Use the code below:

    if (destination === destinationState) {
      console.log("Found => " + destination);
    }

Next, if the current destination is yet to be visited, call the dfs function again (recursively) – but this time, use the destination as the departureState:

    if (!visited.has(destination)) {
      dfs(destination, destinationState, visited)
    }

The destinationState remains constant while the visited Set() is no longer empty. At this point, those destinations in the loop not yet in the visited array go into the stack.

The following is what the dfs function looks like:


function dfs(departureState, destinationState, visited = new Set()) {
  
  visited.add(departureState);
  
  const destinations = connections.get(departureState);

  for (let destination of destinations) {
    if (destination === destinationState) {
      console.log("Found => " + destination);
    }

    if (!visited.has(destination)) {
      dfs(destination, destinationState, visited)
    }
  }
}

To check if there is a connection between two (2) states, say ENUGU and SOKOTO, call the dfs function like this:

dfs("ENUGU", "SOKOTO")

See output below:

Map(11) {
  'ENUGU' => [],
  'ABIA' => [],
  'SOKOTO' => [],
  'NIGER' => [],
  'LAGOS' => [],
  'OGUN' => [],
  'BAYELSA' => [],
  'AKWAIBOM' => [],
  'ANAMBRA' => [],
  'IMO' => [],
  'EBONYI' => []
}
Map(11) {
  'ENUGU' => [ 'LAGOS', 'NIGER' ],
  'ABIA' => [ 'OGUN', 'EBONYI' ],
  'SOKOTO' => [ 'NIGER', 'ANAMBRA' ],
  'NIGER' => [ 'ENUGU', 'SOKOTO', 'ANAMBRA' ],
  'LAGOS' => [ 'ENUGU', 'OGUN' ],
  'OGUN' => [ 'LAGOS', 'ABIA', 'EBONYI', 'BAYELSA' ],
  'BAYELSA' => [ 'OGUN' ],
  'AKWAIBOM' => [],
  'ANAMBRA' => [ 'NIGER', 'SOKOTO' ],
  'IMO' => [],
  'EBONYI' => [ 'OGUN', 'ABIA' ]
}
Found => SOKOTO
Found => SOKOTO

While the output above is the same as the one we got when we ran the bfs function, the process of arriving at this result differs. Try breaking up the code at different points to see the flow of the program.

Conclusion

Data structures and algorithms have become a significant part of software engineering interviews. The map() method is a powerful tool in JavaScript that makes it easier to solve such complex tasks as we have seen in this tutorial.

We began by creating a graph using the map() method. Then we searched for connections between states using the BFS and DFS algorithms.

You can find my code here

It might feel a bit overwhelming if you are new to algorithms and data structures. But with repeated practice, you will get used to it. So if you found it hard to understand what is going on at first, take a break and come back to it again with a clearer head.