The Principles of Functional Programming

In this post, I will lay down the major principles of Functional Programming, starting with the basics and then exploring more advanced concepts.

I'll first talk about why you should bother with Functional Programming, that is when it's useful and when it's not.

We will cover a lot of stuff here, so please go at your own pace. Take some breaks and naps between your reading sessions and do the exercises I propose.

Of course, you can skip sections or go back and fourth depending on your needs.

This post intentionally targets several kind of readers:

Those who know almost nothing about FP but are pretty familiar with JavaScript
Those with an Intermediate knowledge of FP and some familiarity with the paradigm, but who want a clearer picture of the whole and want to explore advanced concepts
Those who know a lot about FP and want a cheatsheet+ to revisit some concepts if needed

I invite you to ponder each sentence carefully instead of rushing through the content like we're all used to.

I hope this post will be an important milestone in your journey into Functional Programming, as well as a source of information to go back to when needed.

Just a heads up, though – this post doesn't constitute a single source of truth but rather an invitation to go further after reading it.

In other words, it's meant to be revisited and expanded with further resources and practice.

I hope to clarify the functional landscape in your mind, spark your interest for what you didn't know, and more importantly, provide useful tools for your day-to-day projects.

Without further ado, let's get started!

Why Functional Programming?

In my opinion, there are 3 major benefits to FP and 3 (little) drawbacks:

Advantages:

More readability, thus maintainability
Less buggy, especially in concurrent contexts
A new way of thinking about problem solving
(Personal bonus) Just great to learn about!

Drawbacks:

Can have performance issues
Less intuitive to work with when dealing with state and I/O
Unfamiliar for most people + math terminology that slows the learning process

Now I'll explain why I think that.

Increased Readability

First, Functional Programming is often more readable because of its declarative nature.

In other words, the code is focused on describing the outcome of the computations, not the computations themselves.

Kyle Simpson phrases it like this:

Declarative code is code that's more focused on describing the "what" outcome. Imperative code (the opposite) is focused on precisely instructing the computer "how" to do something.

Because we spend the vast majority of our time reading code (around 80% of the time I guess) and not writing it, readability is the first thing we should enhance in order to increase our efficiency when programming.

It's also very likely that you'll return back to a project after several weeks of not touching it, so all the context loaded in your short-term memory will have disappeared.

Thus, understanding your imperative code will not be as easy as it was.

The same thing goes for the potential colleagues that work with you on the project.

So readability is a huge advantage for an ever more important purpose: maintainability.

I could stop arguing right there. Increased readability should give you major motivation to learn Functional Programming.

Luckily, that's an advantage that you'll experience more and more as you get familiar with the paradigm.

No need to be an expert. The moment you write a declarative line of code you'll experience it.

Now the second argument.

Less buggy code

Functional programs are less buggy, especially in concurrent contexts.

Because the functional style strives to avoid mutations, shared resources will not have unexpected contents.

For example, imagine that 2 threads access the same variable.

If this variable can be mutated, then, as the programs grow, you'll likely not get what you want when re-accessing it.

In addition, the rise of multiprocessor systems allows multiple threads to execute in parallel.

So now there's also a risk of overlapping (one thread may try to write while the other tries to read).

It's kind of a shame not to leverage the hardware because we're not able to make the software work.

However, JavaScript is single-threaded and my personal experience doesn't expand much beyond it.

Thus, I'm less confident in this argument, but more experienced programmers seem to agree on that fact (for what I've heard/read).

Problem solving

Finally, the last advantage – and more important than you might think – is that Functional Programming gives you a new way of thinking about problem solving.

You might be so used to solving problems using classes and objects (Object-Oriented Programming) that you don't even think there might be a better way to do so.

I'm not saying that Functional Programming is always better.

I'm saying that it will be better in certain cases and that having this knowledge will (re)open your mind and make you a better programmer.

Because now you'll have more tools and an increased capacity to choose the right one for the problem at hand.

I even think that some core principles in FP can translate to problem solving outside the domain of computers.

Let's see the drawbacks now.

Performance issues

The first is that, by applying FP techniques, you can end up using a lot of time and/or memory.

Because you don't want to mutate things, the process is basically to copy the data, then mutate that copy and use it as the current state.

This means that the original data is left untouched but you allocate a bunch of time and memory to make the new copy.

So when you make a lot of copies (really big nested objects) or use techniques like recursion (accumulating layers in the callstack), performance issues may appear.

However, many solutions exist (structural sharing, tail-call optimization) which make poor performance very rare.

Less intuitive

The second drawback is when you need state or I/O operations.

Well, you're gonna say:

Computers are stateful machines! And eventually I'll need to call my database, or display something on the screen, or write a file.

I totally agree.

The thing is to remember that Functional Programming is a style convenient for humans, but machines make imperative operations (aka mutations) all the time.

That's just how it works at the lowest level.

The computer is in one state at a given moment and it changes all the time.

The point of FP is to ease our reasoning about the code which increases the chances that the messy stuff that comes out of it actually works.

And Functional Reactive Programming helps us deal with state (if you want to learn more, there are links at the end of the post).

Even if imperative code seems easier/more intuitive at first sight, you'll eventually lose track. I'm pretty confident that if you make the initial efforts of learning FP, it will pay off.

For I/O – short for Input/Output, that is code that transfers data to or from a computer and to or from a peripheral device – we can't have pure isolated functions anymore.

To deal with that, we can take a Functional Core Imperative Shell approach.

In other words, we want to do as much as we can in a functional way and push back the I/O operations to the outer layer of the program:

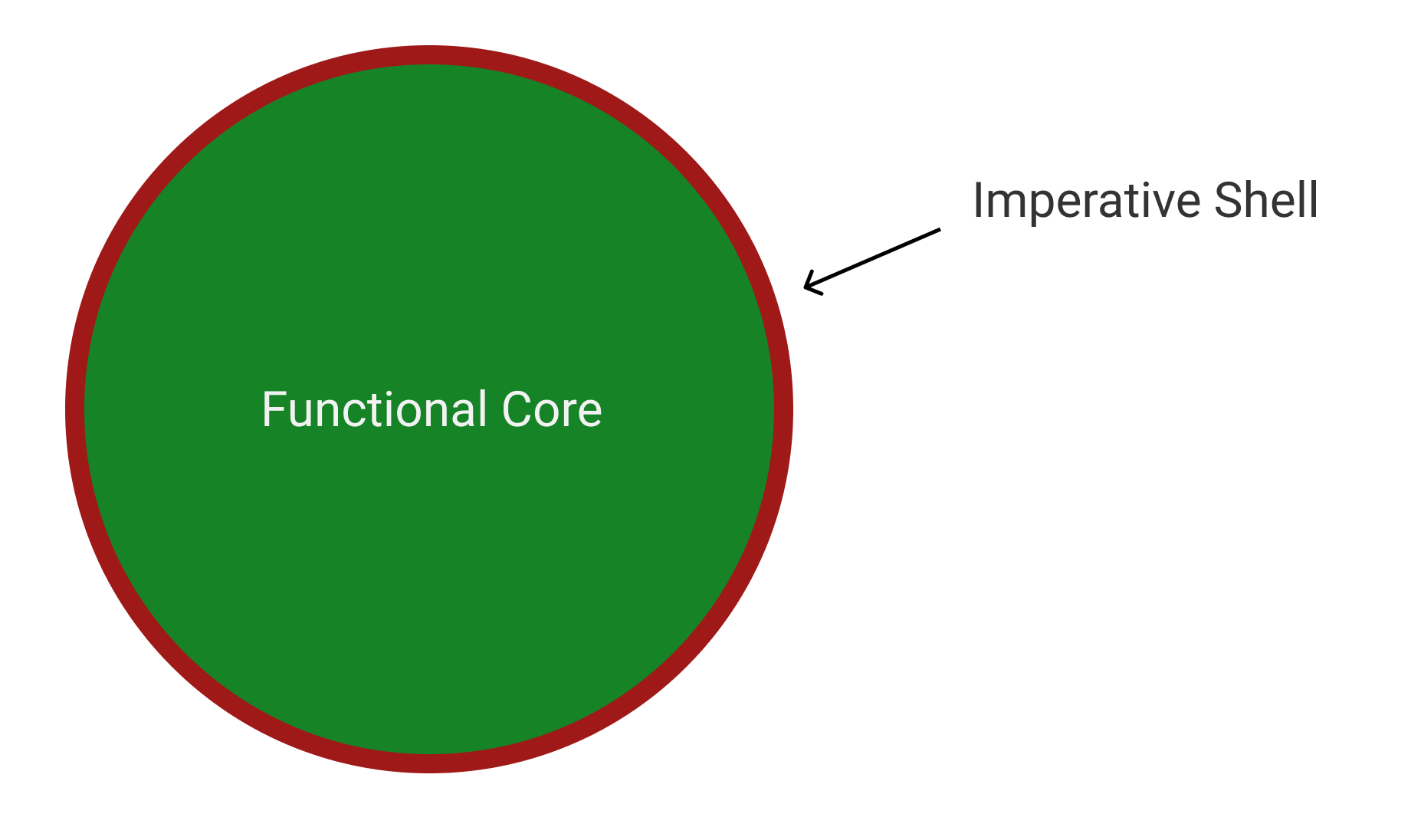
Steeper learning curve

Finally, the last drawback is that Functional Programming is kind of cluttered with math terminology. This often creates unnecessary friction when developers are trying to learn it.

It's likely because this style of programming first appeared in the academic world and stayed there a long time before emerging and becoming more popular.

However, these technical/unfamiliar terms shouldn't make you neglect the very powerful mathematical principles that underlie them.

All in all, I think the strengths of FP outweigh the weaknesses.

And functional programming makes a lot of sense for the majority of general-purpose JavaScript programming.

Just keep in mind that there are few programs with peculiar requirements for which FP is not a good fit. But if that's not your case, there's no reason not to leverage this paradigm.

Now, if you're a total beginner you might be feeling a bit lost. It's ok – bear with me. The following sections will clarify the concepts I referred to here.

Now let's dive into the nuts and bolts of functional programming.

Data, Calculations, and Actions

In FP, you can break down your program in 3 parts: data, calculations and actions.

Data

The data is, well, the data. In our languages, they have different forms, different types.

In JavaScript you have numbers, strings, arrays, objects, and so on. But at the end of the day, they are just bits.

Data are the building blocks of the program. Having none of it is like having no water in an aquatic park.

Then we can do things with the data: calculations or actions.

Calculations

Calculations are mathematical-like transformations of the data.

Functions are a way to create them. You provide it a set of inputs and it returns you a set of outputs.

That's it.

It does nothing outside the function, like in math. The world around the function is not impacted.

In addition, if you feed the function with the same input multiple times, it should always give you the same output.

A common term for this type of function is pure function.

Because of its characteristics, its entire behavior is known in advance. In fact, because it just returns a value, we can treat it as that value, as data.

In other words, we could replace the function call by the value it returns and it would not change the state of the program.

This is called referential transparency. Thus, they're really easy to reason about, and you can use them as function input or output and assign them to variables.

These kinds of functions are called first-class functions. In JavaScript, all functions are first-class.

It's safe to use pure functions because, again, they're like values.

For functions that do more than return a value, you rely on human memory. That's a bad strategy, especially for large software with multiple people working on it.

So you can use pure functions as a replacement for calculations. They are identical.

Now let's talk about actions.

Actions

Of course, we also need functions that impact the outside world, that actually do something. Otherwise, your program would be a calculator without screen.

When a function impacts things outside of itself, we say that it has side-effects. As opposed to pure functions, it is said to be impure.

Common side-effects are assignments/mutations of variables outside the function, logging to the console, making an API call, and so on.

So basically, actions and impure functions are the same.

Here's a simple example to illustrate these concepts:


// ↓ variable
//      ↓ data
let a = 3;

// Calculation / Pure function
const double = (x) => x * 2;

double(a);
// 6

// Action / Impure function
const IncThenPrint = () => {
  // assignment of a variable outside the scope of the function
  a = a + 1;

  // do something (here printing) outside the function
  console.log(a);
};

IncThenPrint();
// console: 4

Data, calculations, and actions in functional programming

In FP, the objective is to separate the data, the calculations, and the actions while striving to do most of the job with calculations.

Why? Because actions rely on the outside world. We don't have total control on it.

Thus, we may get unexpected results/behaviors out of it. So if the majority of your program is made of actions, it quickly becomes a mess.

Taking the previous example, what if somewhere else in the program, someone decided to assign an object to the variable a ?

Well, we'll get an unexpected result when running IncThenPrint because it makes no sense to add 1 to an object:

let a = 3;

// ...
a = { key: "value" };
// ...

// Action / Impure function
const IncThenPrint = () => {
  // assignment of a variable outside the scope of the function
  a = a + 1;

  // do something (here printing) outside the function
  console.log(a);
  // prints: 4
};

IncThenPrint();
// prints: [object Object]1
// (Because JavaScript is a dynamically-typed language, it converts both operands of the + operator
// to strings so it can perform the operation, thus explaining the result.
// But obviously, that not what was intended.)

The ability to differentiate data, calculations, and actions in your program is a fundamental skill to develop.

Mapping

Mapping is a fairly trivial but very important concept in the world of functional programming.

"Mapping from A to B" means going from A to B via some association.

In other words, A points to B by means of some linkage between them.

For example, a pure function maps an input to an output. We can write it like this: input --> output; where the arrow indicates a function.

Another example are objects in JavaScript. They map keys to values.

In other languages, this data structure is often called a "map" or "hash-map", which is more explanatory.

Like the latter term infers, the thing that happens behind the scene is that each key is linked to its value via a hash function. The key is passed to the hash function which returns the index of the corresponding value in the array that stores them all.

Without going into further detail, I wanted to introduce this term because I'll use it throughout this article.

More on side-effects

Before we move on, I want to go deeper into side-effects in JavaScript and showcase a vicious pitfall that you may not be aware of.

To remind ourselves, saying that a function has side-effects is the same as saying, "When this function runs, something outside of its scope will change."

Like I said, it can be logging to the console, making an API call, changing an outer variable, etc.

Let's see an example of the latter:

let y;

const f = (x) => {
  y = x * x;
};

f(5);
y; // 25

That's pretty easy to grasp.

When f runs, it assigns a new value to the outer variable y, which is a side-effect.

A pure version of this example would be:

const f = (x) => x * x;

const y = f(5);
// 25

But there's another way to change an outer variable that's more subtle:

let myArr = [1, 2, 3, { key: "value" }, "a string", 4];

const g = (arr) => {
  let total = 0;

  for (let i = 0; i < arr.length; i++) {
    if (Number.isNaN(Number(arr[i]))) {
      arr[i] = 0;
    }
    total += arr[i];
  }

  return total;
};

g(myArr);
// 10
myArr;
// [1, 2, 3, 0, 0, 4]
// Oops, all elements that were not numbers have been changed to 0 !

Why is that?

In JavaScript, when assigning a value to a variable or passing it to a function, it's automatically copied.

But there's a distinction to make here.

Primitive values (null, undefined, strings, numbers, booleans and symbols) are always assigned/passed by value-copy.

In contrast, compound values like objects, arrays and functions (by the way, arrays and functions are objects in JavaScript, but I don't refer to them as objects for clarity) create a copy by reference on assignment or passing.

So in the previous example, the value passed to g is a compound one, the array myArr.

What happens is that g stores the memory address of myArr in arr, the parameter's name used in the function's body.

In other words, there's no value-copy of each elements in myArr like you would expect. Thus, when you manipulate or change arr, it actually goes to myArr memory's location and perform whatever computation you specified.

So yeah, be aware of that quirk.

Exercises (Set 1)

In the snippet below, find the pure functions and the impure ones:

// a
const capitalizeFirst = (str) => str.charAt(0).toUpperCase() + str.slice(1);

// b
const greeting = (persons) => {
  persons.forEach((person) => {
    const fullname = `${capitalizeFirst(person.firstname)} ${capitalizeFirst(
      person.lastname
    )}`;

    console.log(`Hello ${fullname} !`);
  });
};

// c
const getLabels = async (endpoint) => {
  const res = await fetch("https://my-database-api/" + endpoint);
  const data = await res.json();
  return data.labels;
};

// d
const counter = (start, end) => {
  return start === end
    ? "End"
    : // e
      () => counter(start + 1, end);
};

2. Convert this snippet into a pure one (you can make more than one function if you feel the need to):

const people = [
  { firstname: "Bill", lastname: "Harold", age: 54 },
  { firstname: "Ana", lastname: "Atkins", age: 42 },
  { firstname: "John", lastname: "Doe", age: 57 },
  { firstname: "Davy", lastname: "Johnson", age: 34 },
];

const parsePeople = (people) => {
  const parsedPeople = [];

  for (let i = 0; i < people.length; i++) {
    people[i].firstname = people[i].firstname.toUpperCase();
    people[i].lastname = people[i].lastname.toUpperCase();
  }

  const compareAges = (person1, person2) => person1.age - person2.age;

  return people.sort(compareAges);
};

parsePeople(people);
// [
//   {firstname: "DAVY", lastname: "JOHNSON", age: 34},
//   {firstname: "ANA", lastname: "ATKINS", age: 42},
//   {firstname: "BILL", lastname: "HAROLD", age: 54},
//   {firstname: "JOHN", lastname: "DOE", age: 57},
// ]

Check answers.

Immutability

Like we've seen previously, a common side-effect is to mutate a variable.

You don't want to do that in functional programming. So an important characteristic of a functional program is the immutability of data.

In functional languages like Clojure and Haskell, this feature is built-in – you have no way to mutate the data unless the language allows it. In any case, you must consciously opt to do so.

But in JavaScript, that's not the case.

So it's more about having the "immutability" mindset than a real robust implementation of this feature.

What this means is that you will basically make copies of the data you want to work on.

In the first section, we saw that JavaScript functions automatically make copies of the arguments passed. While primitive values are copied by value, compound values are only copied by reference, so it's still possible to mutate them.

Thus, when working with an object/array in a function, you should make a copy and then operate on it.

By the way, notice that some built-in functions doesn't mutate the value it's called upon, while others do.

For example, Array.prototype.map, Array.prototype.filter, or Array.prototype.reduce are don't mutate the original array.

On the other hand, Array.prototype.reverse and Array.prototype.push are mutate the original array.

You can find out if a built-in function mutates the value it's called upon or not in the documentation, so check it out if you're not sure.

That's annoying, and ultimately not perfectly safe.

Shallow vs. deep copies

Since ES6, it's easy to make object/array copies through spread notation, Array.from(), Object.assign().

For example:

// arrays
const fruits = ["apple", "strawberry", "banana"];
const fruitsCopy = [...fruits];
fruitsCopy[0] = "mutation";
// fruitsCopy: ['mutation', 'strawberry', 'banana']
// fruits (not mutated): ['apple', 'strawberry', 'banana']

// objects
const obj = { a: 1, b: 2, c: 3 };
const objCopy = { ...obj };
objCopy.a = "mutation";
// objCopy: {a: "mutation", b: 2, c: 3}
// obj (not mutated): {a: 1, b: 2, c: 3}
console.log(obj);
console.log(objCopy);

That's cool but there's a gotcha.

Spread arrays/objects only have there first level copied by value, also known as a shallow copy.

So all subsequent levels are still mutable:

// But with nested objects/arrays, that doesn't work
const nestedObj = { a: { b: "canBeMutated" } };
const nestedObjCopy = { ...nestedObj };
nestedObjCopy.a.b = "hasBeenMutated!";
console.log(nestedObj);
console.log(nestedObjCopy);
// nestedObjCopy: {a: {b: "hasBeenMutated!"}}}
// nestedObj (mutated): {a: {b: "hasBeenMutated!"}}

To resolve this problem, we need a custom function to do deep copies. This article discusses multiple solutions.

Here's a shortened version of the custom function proposed in it:

// works for arrays and objects
const deepCopy = (obj) => {
  if (typeof obj !== "object" || obj === null) {
    return obj; // Return the value if obj is not an object
  }

  // Create an array or object to hold the values
  let newObj = Array.isArray(obj) ? [] : {};

  for (let key in obj) {
    // Recursively (deep) copy for nested objects, including arrays
    newObj[key] = deepCopy(obj[key]);
  }

  return newObj;
};

const nestedObj = {
  lvl1: { lvl2: { lvl3: { lvl4: "tryToMutateMe" } } },
  b: ["tryToMutateMe"],
};
const nestedObjCopy = deepCopy(nestedObj);

nestedObjCopy.lvl1.lvl2.lvl3.lvl4 = "mutated";
nestedObjCopy.b[0] = "mutated";

console.log(nestedObj);
// { lvl1: { lvl2: { lvl3: { lvl4: "tryToMutateMe" } } }, b: ["tryToMutateMe"]}
console.log(nestedObjCopy);
// { lvl1: { lvl2: { lvl3: { lvl4: "mutated" } } }, b: ["mutated"]}

If you already use a library that provides functional utilities, it's likely that it has one to do deep copies. I personally like Ramda. See its clone function.

If the difference between shallow and deep copies still isn't clear, check this out.

Now let's talk about performance.

Obviously, making copies doesn't come without a cost.

For performance-sensitive parts of the program, or in cases where changes happen frequently, creating a new array or object (especially if it contains lots of data) is undesirable for both processing and memory reasons.

In these cases, using immutable data structures from a library like Immutable.js is probably a better idea.

They use a technique called structural sharing which I referred to when talking about the downsides of FP earlier in this post.

Check out this great talk to learn more.

Dealing with immutable data is thus, in my opinion, the second skill to have in your functional programmer tool belt.

Composition and Currying

Composition

Unsurprisingly, the fundamental building blocks of a functional program are functions.

Because your functions are free of side-effects and considered first-class, we can compose them.

Like I said, first-class means that they're treated as regular data structures, possibly being assigned to variables, passed as arguments, or returned from other functions.

Composition is a powerful idea.

From tiny little functions, you can add up their functionalities to form a more complex one, but without the pain of laying it down upfront.

In addition, you get greater flexibility because you can easily rearrange your compositions.

Being backed up by mathematical laws, we know that everything will work if we follow them.

Let's introduce some code to make things concrete:

const map = (fn, arr) => arr.map(fn);

const first = (xs) => xs[0];

const formatInitial = (x) => x.toUpperCase() + ".";

const intercalate = (sep, arr) => arr.join(sep);

const employees = ["Yann", "Brigitte", "John", "William"];

const initials = intercalate("\n", map(formatInitial, map(first, employees)));
// Y.
// B.
// J.
// W.

Ouch – there's a little bit of nesting here.

Take some time to understand what's going on. As you can see, there are function calls passed as arguments to outer functions.

With the power of map, we essentially composed the functionalities of first, formatInitial, and join to eventually apply them on the employees array.

Pretty cool!

But as you can see, nesting is annoying. It makes things harder to read.

Currying

To flatten that stuff and make composition a breeze, we have to talk about currying.

This term may scare you, but don't worry, it's just jargon for a simple idea: feeding a function one argument at a time.

Usually, when we make a function call, we provide all the arguments at once and get back the result:

const add = (x, y) => x + y;

add(3, 7);
// 10

But what if we could pass only one argument and provide the second one later?

Well, we can do that by currying add like so:

const add = (x) => (y) => x + y;

const addTo3 = add(3);
// (y) => 3 + y

// ...later
addTo3(7);
// 10

This can be useful if we don't have all the arguments yet.

You might not understand why we wouldn't have all the arguments beforehand, but you'll see later.

Thanks to closures, we're preloading the function with its arguments step-by-step until we eventually run it.

If you have a hard time grasping the concept of closure, check this, then this to go deeper.

In short, closure allows an inner function to access variables of an outer function's scope. That's why we can access x in the scope of addTo3 which comes from the outer scope, add.

Often you don't want to bother writing your functions in this special form. In addition, you can't always write them this way, for example, when you use external library functions and virtually anything you don't write but use all the same.

For this reason, there's a common helper to curry a function (from Kyle Simpson book YDKJS):

const curry = (fn, arity = fn.length) => {
  return (function nextCurried(prevArgs) {
    return function curried(...nextArgs) {
      const args = [...prevArgs, ...nextArgs];

      return args.length < arity ? nextCurried(args) : fn(...args);
    };
  })([]);
};

curry takes a function and a number called arity (optional).

The arity of a function is the number of arguments it takes.

In the case of add, it's 2.

We need that information to know when all the arguments are there, and thus decide to run the function or return another curried function that will take the remaining ones.

So let's refactor our example with add:

const add = curry((x, y) => x + y);

const addTo3 = add(3);

addTo3(7);
// 10

Or we can still call add with all its arguments directly:

const add = curry((x, y) => x + y);

add(3, 7);
// 10

Partial application

Actually, curried strictly means "takes one argument at a time", no more, no less.

When we can provide the number of arguments we want, we're actually talking about partial application.

Thus, currying is a constrained form of partial application.

Let's see a more explicit example of partial application compared to currying:

const listOf4 = curry((a, b, c, d) => `1. ${a}\n2. ${b}\n3. ${c}\n4. ${d}`);

// strict currying

const a = listOf4("First")("Second")("Third")("Fourth");
// or
const b = listOf4("First");
// later
const c = b("Second")("Third");
// later
const d = c("Fourth");

// partial application

const e = listOf4("First", "Second", "Third", "Fourth");
// or
const b = listOf4("First");
// later
const c = b("Second", "Third");
// later
const d = c("Fourth");

Do you see the difference?

With currying, you should provide one argument at a time. If you want to feed more than one argument, then you need to make a new function call, hence the pair of parentheses around each argument.

Honestly, that's just a matter of style.

It seems a bit awkward when you're not used to it, but on the other hand, some people find the partial application style to be messy.

The curry helper I introduced allows you to do both.

It stretches the real definition of currying, but I prefer to have both functionalities and don't like the name looseCurry that Kyle Simpson used in is book. So, I cheated a little bit.

Just keep the differences in mind and be aware that curry helpers you find in libraries probably follow the strict definition.

Data comes last

A final point I want to make is that we usually place the data as the last argument.

With the previous functions I used, it's not obvious because all arguments are data. But take a look at this:

const replace = curry((regex, replacement, str) =>
  str.replace(regex, replacement)
);

You can see that the data (str) is in the last position because it's likely to be the last thing we'll want to pass through.

You will see that this is the case when composing functions.

Bring it all together

Now to take advantage of currying and flatten our nested jumble from before, we also need a helper for composition.

You guessed it, it's called compose!:

const compose = (...fns) =>
  fns.reverse().reduce((fn1, fn2) => (...args) => fn2(fn1(...args)));

compose takes functions as arguments and returns another function which takes the argument(s) to pass through the whole pipeline.

Functions are applied from right to left because of fns.reverse().

Because compose returns a function that takes the future argument(s), we can freely associate our functions without calling them, which allow us to create intermediate functions.

So with our initial example:

const map = (fn, arr) => arr.map(fn);

const first = (xs) => xs[0];

const formatInitial = (x) => x.toUpperCase() + ".";

const intercalate = (sep, arr) => arr.join(sep);

const getInitials = compose(formatInitial, first);

const employees = ["Yann", "Brigitte", "John", "William"];

const initials = intercalate("\n", map(getInitials, employees));
// Y.
// B.
// J.
// W.

first and formatInitial already take one argument.

But map and intercalate take 2 arguments, so we can't include them as is in our compose helper because only one argument will be passed. In this case it's an array that both take as a final argument (remember, data is the last thing to get passed).

It would be nice to give map and intercalate their respective first argument in advance.

Wait a minute – we can curry them!:

// ...

const map = curry((fn, arr) => arr.map(fn));

const intercalate = curry((sep, arr) => arr.join(sep));

const formatInitials = compose(
  intercalate("\n"),
  map(formatInitial),
  map(first)
);

const employees = ["Yann", "Brigitte", "John", "William"];

const initials = formatInitials(employees);
// Y.
// B.
// J.
// W.

So clean!

Like I said, compose makes a pipeline with the functions we give it, calling them from right to left.

So let's visualize what happens when formatInitials(employees) is parsed:

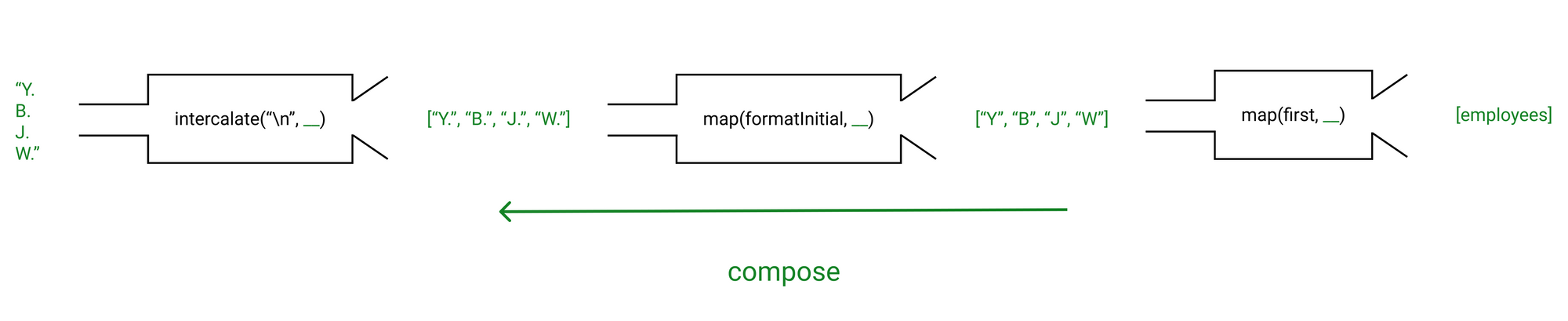
Personally, I prefer when it goes from left to right, because when writing the function, I like to think about what transformation to apply first, write it down, then repeat until the end of the pipeline.

Whereas with compose, I have to step back to write the next transformation. That just breaks the flow of my thinking.

Fortunately, it's not complicated to tweak it in order to go from left to right.

We just have to get rid of the .reverse() part.

Let's call our new helper pipe:

const pipe = (...fns) => fns.reduce((fn1, fn2) => (...args) => f2(f1(...args)));

So if we refactor the previous snippet, we get:

const formatInitials = pipe(map(first), map(formatInitial), intercalate("\n"));

For the visualization, same thing as compose but in reverse order:

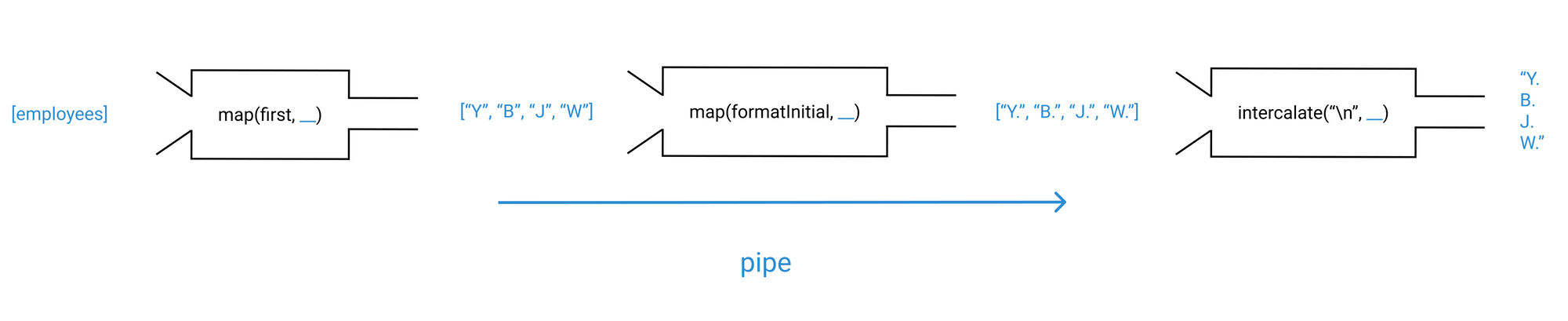
Hindley-Milner type signatures

As you know, a complete program ends up with quite a few functions.

When you plunge back into a project after several weeks, you don't have the context to easily understand what each function does.

To counter that, you reread only the parts you need. But this can be quite tedious.

It would be nice to have a quick and powerful way to document your functions and explain what they do at a glance.

That's where type signatures come in. They are a way to document how a function operates and its inputs and outputs.

For example:

// ↓ function name
//                  ↓ input
//                            ↓ output
// formatInitial :: String -> String
const formatInitial = (x) => x.toUpperCase() + ".";

Here we see that formatInitial takes a String and returns a String.

We don't care about the implementation.

Let's look at another example:

// first :: [a] -> a
const first = (xs) => xs[0];

Types can be expressed with variables (usually a, b, etc.) and the brackets means "an array of" whatever is inside.

So we could literally read this signature like this:

first takes an array of a and returns an a, where a can be of any type.

But because the type taken as input is the same as the one returned as output, we use the same variable.

If the output had another type, we would have used b:

// imaginaryFunction :: a -> b

Warning!

That doesn't ensure that a and b are different types. They still can be the same.

Finally, let's see the case of intercalate which is a bit more complex:

// intercalate :: String -> [a] -> String
const intercalate = curry((sep, arr) => arr.join(sep));

OK, here there are 2 arrows, which can be replaced by "returns...".

They indicate functions.

So intercalate takes a String then returns a function which takes an array of a, which returns a String.

Wow, that's hard to keep track of.

We could have written the signature like this:

// intercalate :: String -> ([a] -> String)

Now it's more obvious that it first returns a function, which is in parentheses here. And then that function will take [a] as input and return String.

But we usually don't use them for clarity sake. Basically, if you stumble upon a signature of the form:

// imaginaryFunction :: a -> b -> c -> d -> e

// or

// imaginaryFunction :: a -> (b -> (c -> (d -> e)))

// ...you see how parens nesting affects readability

e, the type on the right side, is the output.

And everything before are inputs given one-by-one, which indicates that the function is curried.

Nowadays, we usually have type systems like TypeScript or Flow, and the IDE is able to give us the type signature of a function when we hover over its name. Thus, it might be unnecessary to write them as comments in your code.

But this remains a nice tool to have in your toolkit because a lot of functional libraries out there use these type signatures in their documentations. And idiomatic functional languages (like Haskell) use them heavily.

So if you give them a shot, you will hopefully not be completely lost.

Pat yourself on the back for having read this far.

You should now have the ability to work with higher-order functions. Higher-order functions are simply functions that take functions as inputs and/or return them.

Indeed, that's exactly what we did.

For example, curry is an higher-order function because it takes a function as input and returns one as output.

compose, pipe, map, and reduce are all higher-order functions because they take at least one function as input.

They are pretty cool because they allow to create very powerful abstractions.

Enough nattering. Let's get some practice.

Exercises (Set 2)

Given a string of the form:

const input = "Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.";

...and these helpers:

// filter :: (a -> Boolean) -> [a] -> [a]
const filter = curry((fn, arr) => arr.filter(fn));

// removeDuplicates :: [a] -> [a]
const removeDuplicates = (arr) => Array.from(new Set(arr));

// getChars :: String -> [Character]
const getChars = (str) => str.split("");

// lowercase :: String -> String
const lowercase = (str) => str.toLowerCase();

// sort :: [a] -> [a]
const sort = (arr) => [...arr].sort();

Create a function getLetters that returns all the letters in a string without duplicates, in alphabetical order, and in lowercase.

The goal is to use compose and/or pipe:

// getLetters :: String -> [Character]
const getLetters = ...

Note: You may have to create intermediate functions before the final one.

2. Imagine you have an object with groups' names as keys and arrays of objects representing people as values:

{
  "groupName": [
    {firstname: "John", lastname: "Doe", age: 35, sex: "M"},
    {firstname: "Maria", lastname: "Talinski", age: 28, sex: "F"},
    // ...
  ],
  // ...
}

Create a function that returns an object of the form:

{
  "groupName": {
    "medianAgeM": 34,
    "medianAgeF": 38,
  },
  // ...
}

Where medianAgeM is the median age of men in the group and medianAgeF the one of women.

Here's some helpers:

// map :: (a -> b) -> [a] -> [b]
const map = curry((fn, arr) => arr.map(fn));

// getEntries :: Object -> [[Key, Val]]
const getEntries = (o) => Object.entries(o);

// fromEntries:: [[Key, Val]] -> Object
const fromEntries = (entries) => Object.fromEntries(entries);

// mean :: Number -> Number -> Number
const mean = curry((x, y) => Math.round((x + y) / 2));

// reduceOverVal :: (b -> a -> b) -> b -> [Key, [a]] -> [Key, b]
const reduceOverVal = curry((fn, initVal, entry) => [
  entry[0],
  entry[1].reduce(fn, initVal),
]);

You may have to create intermediate functions before the final one, and like before, try to use compose and pipe:

// groupsMedianAges :: Object -> Object
const groupsMedianAges = ...

3. Find the type signature of reduce:

const reduce = curry((fn, initVal, arr) => arr.reduce(fn, initVal));

4. Find the type signature of curry:

const curry = (fn, arity = fn.length) => {
  return (function nextCurried(prevArgs) {
    return function curried(...nextArgs) {
      const args = [...prevArgs, ...nextArgs];

      return args.length < arity ? nextCurried(args) : fn(...args);
    };
  })([]);
};

Check answers.

Working with boxes: From Functors to Monads

You may already be stressed out by the title of this section. You might be thinking, "What the heck are 'Functors' and 'Monads'?"

Or maybe you've heard about monads because they're famously "difficult" to understand.

Unfortunately, I can't predict that you will definitely understand these concepts, or effectively apply them in whatever work you do.

In fact, if I talk about them at the end of this tutorial, it's because I think they're very powerful tools that we don't need very often.

Here's the reassuring part: Like anything in the world, they're not magic.

They follow the same rules of physics (and more specifically computer science and math) as everything else.

So at the end of the day, they're understandable. It just requires the right amount of time and energy.

In addition, they essentially build upon what we've previously talked about: types, mapping and composition.

Now, find that tube of perseverance in your toolkit and let's get started.

Why use boxes?

We want to make our program with pure functions. Then we use composition to specify in which order to run them over the data.

However, how do we deal with null or undefined? How do we deal with exceptions?

Also, how do we manage side-effects without losing control, because one day we'll need to perform them?

The first two cases involve branching. Either the value is null and we do this, or we do that. Either there's an error and we do this, or a success and we do that.

The usual way to deal with branching is control flow.

However, control flow is imperative. It describes "how" the code operates.

So functional programmers came up with the idea of using a box that contains one of two possible values.

We use that box as input/output to functions regardless of what's inside.

But because those boxes also have specific behaviors that abstract function application, we can apply a function over a box and it will decide how to actually perform it depending on its inner value.

Thus, we don't have to adapt our functions to the data. We don't have to clutter them with logic that doesn't belong to.

Things like:

const myFunc = (x) => {
  // ...
  if (x !== null) {
    // ...
  } else {
    // ...
  }
};

With that, we can implement branching (and other stuff) while using only functions and preserve composition.

The boxes we'll see, named Algebraic Data Types (ADT), enable us to do more while keeping the data and the functions separate.

Functors and monads are indeed Algebraic Data Types.

Functors

Functors are containers/data structures/types that hold data along with a map method.

This map method allow us to apply a function on the value(s) contained in the functor. What's returned is the same functor but containing the result of the function call.

Let's introduce Identity, the simplest functor:

We could implement it with a class, but I'll use regular functions here:

const Identity = (x) => ({
  inspect: () => `Identity(${x})`,
  map: (fn) => Identity(fn(x)),
  value: x,
});

// add5 :: Number -> Number
const add5 = (x) => x + 5;

const myFirstFunctor = Identity(1);

myFirstFunctor.map(add5);
// Identity(6)

You see? Not that complicated!

Identity is the equivalent of the identity function but in the world of functors.

identity is a well-known function in FP that may seem useless at first sight:

// identity :: a -> a
const identity = (x) => x;

It does nothing on the data, just returns it as is.

But it can be useful when doing stuff like composition because sometimes, you don't want to do anything with the data, just pass it through.

And because composition works with functions and not raw values, you need to wrap them into the identity function.

Identity serves the same purpose but when composing functors.

Pointed

A pointed functor is one that has an of (aka pure, unit) method.

So with Maybe that gives us:

const Maybe = {Just, Nothing, of: Just};

of is meant to place a given value into the default minimum context of the functor.

You may ask:

Why Just and not Nothing ?

When using of, we expect to be able to map right away.

If we use Nothing, it would ignore everything we map.

of expects you to insert a "successful" value.

Thus, you can still shoot yourself in the foot by inserting undefined, for example, and then map a function that doesn't expect this value:

Maybe.of(undefined).map((x) => x + 1);
// Just(NaN)

Let's introduce another functor to better understand when it's useful:

const IO = (dangerousFn) => ({
  inspect: () => `IO(?)`,
  map: (fn) => IO(() => fn(dangerousFn())),
});

IO.of = (x) => IO(() => x);

Unlike Just, IO don't get a value as is but needs it wrapped in a function.

Why is that?

I/O stands for Input/Output.

The term is used to describe any program, operation, or device that transfers data to or from a computer and to or from a peripheral device.

So it's intended to be used for input/output operations, which are side-effects because they rely on/affect the outside world.

Querying the DOM is an example:

// getEl :: String -> DOM
const getEl = (sel) => document.querySelector(sel);

This function is impure because given a same input, it can return different outputs:

getEl("#root");
// <div id="root"></div>

// or

getEl("#root");
// <div id="root">There's text now !</div>

// or

getEl("#root");
// null

Whereas by inserting an intermediate function, getEl returns always the same output:

// getEl :: String -> _ -> DOM
const getEl = (sel) => () => document.querySelector(sel);

getEl("#root");
// function...

Whatever the argument passed is, getEl will always return a function, allowing it to be pure.

However, we're not magically erasing the effect because now, it's the returned function that's impure.

We get purity out of laziness.

The outer function only serves as a protective box that we can pass around safely. When we are ready to release the effect, we call the returned function's function.

And because we want to be careful doing so, we name the function unsafePerformIO to remind the programmer that it's dangerous.

Until then, we can do our mapping and composition stuff peacefully.

So that's the mechanism used by IO.

If you pass a value directly to it, it must be a function with the same signature as the one that getEl returns:

const a = IO(() => document.querySelector("#root"));

// and not:

const invalid = IO(document.querySelector("#root"));

But as you can imagine, it quickly becomes tedious to always wrap our value in a function before passing it into IO.

Here's where of shines – it will do that for us:

const betterNow = IO.of(document.querySelector("#root"));

That's what I meant by default minimum context.

In the case of IO, it's wrapping the raw value in a function. But it can be something else, it depends of the functor in question.

Exercises (Set 3)

Write a function uppercaseF that uppercase a string inside a functor:

// uppercaseF :: Functor F => F String -> F String
const uppercaseF = ...

2. Use the uppercaseF function you previously built, maybe, and safeProp to create a function that retrieves the name of a user and prints an uppercased version of it.

The user object has this form:

{
  name: "Yann Salmon",
  age: 18,
  interests: ["Programming", "Sport", "Reading", "Math"],
  // ...
}

// safeProp :: String -> Object -> Maybe a

// maybe :: c -> (a -> b) -> Maybe a -> b | c

// printUsername :: User -> _
const printUsername = ...

Check answers.

Applicatives

If you work with functors, you will stumble upon situations where you have multiple functors containing values on which you would like to apply a function:

// concatStr :: String -> String -> String
const concatStr = curry((str1, str2) => str1 + str2);

const a = Identity("Hello");

const b = Identity(" world !");

Unfortunately, we can't pass functors as arguments to concatStr because it expects strings.

The Applicative interface solves that problem.

A functor that implements it is one that implements an ap method. ap takes a functor as argument and returns a functor of the same type.

Within the returned functor, there will be the result of mapping the value of the functor ap was called on, over the value of the functor previously taken as argument.

I know that's a lot to digest. Take some time and let that sink in.

Let's continue our previous snippet to see it in action:

// concatStr :: String -> String -> String
const concatStr = curry((str1, str2) => str1 + str2);

const a = Identity("Hello");

const b = Identity(" world !");

const c = a.map(concatStr);
// Identity(concatStr("Hello", _))

const result = c.ap(b);
// Identity("Hello world !")

First, we map concatStr over a. What happens is that concatStr("Hello") is called and becomes the inner value of c, still an Identity functor.

And remember, what does return concatStr("Hello")? Another function that waits for the remaining arguments!

Indeed, concatStr is curried.

Note that currying is necessary in order to use this technique.

Then, like I said, ap maps the value of the functor it's called on (in this case c, so it maps concatStr("Hello")) over the value of the functor taken as argument (here it's b containing " world !").

So result ends up being an Identity functor (same type as b) containing the result of concatStr("Hello")(" world !"), that is "Hello world !"!

Here's the implementation:

const Identity = (x) => ({
  inspect: () => `Identity(${x})`,
  // Functor interface
  map: (fn) => Identity(fn(x)),
  // Applicative interface
  ap: (functor) => functor.map(x),
  value: x,
});

// Pointed interface
Identity.of = (x) => Identity(x);

As you can see, the functor ap is called on must contain a function. Otherwise it wouldn't work. In our previous example, that was the c step.

If we inline everything, we get:

// concatStr :: String -> String -> String
const concatStr = curry((str1, str2) => str1 + str2);

const result = Identity("Hello").map(concatStr).ap(Identity(" world !"));
// Identity("Hello world !")

There's an interesting mathematical property about ap:

F(x).map(fn) === F(fn).ap(F(x));

The left side of the equality corresponds to what we did previously.

So following the right side, result could also be written like this:

const result = Identity(concatStr)
  .ap(Identity("Hello"))
  .ap(Identity(" world !"));

Take the time to reread if you feel overwhelmed.

The latter version ressembles more to a regular function call than the previous. We're feeding concatStr with its arguments in a left-to-right manner:

And all of that happens inside our protecting container.

Finally, we can further clean up this process with parametrization.

A function called liftA2 do that:

// liftA2 :: Apply functor F => (a -> b -> c) -> F a -> F b -> F c
const liftA2 = curry((fn, F1, F2) => F1.map(fn).ap(F2));

// ...

const result = liftA2(concatStr, Identity("Hello"), Identity(" world !"));

I'm sure we can agree that this name is really awkward.

I guess it made sense for the pioneers of Functional Programming, who were probably "math" people.

But anyway, you can think of it as "lifting" a function and its arguments, then putting them into a functor in order to ap each one on the other.

However, this metaphor is just partially true because arguments are already given within their container.

The interesting part is the body of the function.

You can notice that it uses the left-hand side of the mathematical property we saw earlier.

If we implement it using the right-hand side, we need to know what type of functor F1 and F2 are because we need to wrap the function with the same:

const liftA2 = curry((fn, F1, F2) => F(fn).ap(F1).ap(F2));
//                                   ↑ what's F ? We need the precise constructor.

So by using the left version, we abstract the functor type for free.

Now you might think, "OK, but what if the function requires 3, 4, or more arguments?"

If that's the case, you can build variants just by extending our previous liftA2:

// liftA3 :: Apply functor F => (a -> b -> c -> d) -> F a -> F b -> F c -> F d
const liftA3 = curry((fn, F1, F2, F3) => F1.map(fn).ap(F2).ap(F3));

// liftA4 :: Apply functor F => (a -> b -> c -> d -> e) -> F a -> F b -> F c -> F d -> F e
const liftA4 = curry((fn, F1, F2, F3, F4) => F1.map(fn).ap(F2).ap(F3).ap(F4));

// take3Args :: String -> String -> Number -> String
const take3Args = curry(
  (firstname, lastname, age) =>
    `My name is ${firstname} ${lastname} and I'm ${age}.`
);

// take4Args :: a -> b -> c -> d -> [a, b, c, d]
const take4Args = curry((a, b, c, d) => [a, b, c, d]);

liftA3(take3Args, Identity("Yann"), Identity("Salmon"), Identity(18));
// Identity("My name is Yann Salmon and I'm 18.")

liftA4(take4Args, Identity(1), Identity(2), Identity(3), Identity(4));
// Identity([1, 2, 3, 4])

As you can notice, A* refers to the number of arguments.

Wow! We've covered a bunch of things.

Again, I want to congratulate you for the time and attention you've given so far.

We almost have a fully fledged toolbox for resolving real world problems in a functional way.

We now need to explore the Monad interface.

Exercises (Set 4)

Consider this user object for the next 2 exercises:

const user = {
  id: "012345",
  name: "John Doe",
  hobbies: ["Cycling", "Drawing"],
  friends: [
    {name: "Mickael Bolp", ...},
    // ...
  ],
  partner: {name: "Theresa Doe", ...},
  // ...
}

Create a function that returns a phrase describing the couple if the user has a partner using the given helpers and ap:

// safeProp :: String -> Object -> Maybe a
const safeProp = curry((prop, obj) =>
  obj[prop] === undefined || obj[prop] === null
    ? Maybe.Nothing()
    : Maybe.Just(obj[prop])
);

// getCouplePresentation :: User -> User -> String
const getCouplePresentation = curry(
  (name1, name2) => `${name1} and ${name2} are partners.`
);

// getName :: User -> String
const getName = (user) => user.name;
// I could have written: const getName = safeProp("name")
// but I didn't and that's intentional.
// We assume that a user always has a name.

const couple = ...

2. Refactor the previous answer using liftA2 (check out the answer of the previous question before):

// liftA2 :: Apply functor F => (a -> b -> c) -> F a -> F b -> F c
const liftA2 = curry((fn, F1, F2) => F1.map(fn).ap(F2));

const couple = ...

Check answers.

Monads

In the exercises just before, I gave the helper getName whereas we could have derived it from safeProp.

The reason I did that is because safeProp returns a Maybe functor.

Thus, by trying to get the partner's name of a user, we end up with 2 nested Maybe functors:


const getPartnerName = pipe(safeProp("partner"), map(safeProp("name")));
// Maybe(Maybe("Theresa Doe"))

Let's see another example where this problem get even worse:

// getUser :: Object -> IO User
const getUser = ({ email, password }) => IO.of(db.getUser(email, password));

// getLastPurchases :: User -> IO [Purchase]
const getLastPurchases = (user) => IO.of(db.purchases(user));

// display :: [Purchase] -> IO _
const display = "some implementation";

// displayUserPurchases :: Object -> IO _
const displayUserPurchases = pipe(
  getUser,
  map(getLastPurchases),
  map(map(display))
);

displayUserPurchases({ email: "johndoe@whatever.com", password: "1234" });
// IO(IO(IO _))

How to get rid of these layers of container that enforce us to do nested map that impairs readability ?

Monads to our rescue! Monads are functors that can flatten.

Again, like regular functors, you will probably not use them very often.

However, they're powerful abstractions that bundle a specific set of behaviors with a value.

They're data structures backed up by mathematical laws which make them extremely predictable and reliable.

In addition, laws like composition or associativity tell us that we can do the same thing while making the operations in a different way.

Remember what we saw with Applicatives and ap:

F(x).map(fn) === F(fn).ap(F(x));

These can be helpful because certain variants might be more efficient computationaly.

The thing is that the way we prefer to write programs may differ from the way they should be written if we wanted them to be efficient as much as possible.

So because these laws ensure us that all variants do the same thing, we can write how we like and ask the compiler to use the more efficient variant later.

That's why I didn't bothered you with these laws very much. But be aware of their utility (which certainly extends beyond that).

Going back to our monads, the flattening behavior is usually implemented with a chain (aka flatMap, bind, >==) method:

const Identity = (x) => ({
  inspect: () => `Identity(${x})`,
  // Functor interface
  map: (fn) => Identity(fn(x)),
  // Applicative interface
  ap: (functor) => functor.map(x),
  // Monad interface
  chain: (fn) => fn(x),
  value: x,
});

// Pointed interface
Identity.of = (x) => Identity(x);

// chain :: Monad M => (a -> M b) -> M a -> M b
const chain = curry((fn, monad) => monad.chain(fn));

const getPartnerName = pipe(safeProp("partner"), chain(safeProp("name")));

In the case of Identity, chain is like map but without a new Identity functor surrounding it.

You may think, "That defeats the purpose, we'll get back a value unboxed!"

But, we won't because fn is meant to return a functor.

Look at the type signature of this chain helper:

// chain :: Monad M => (a -> M b) -> M a -> M b
const chain = curry((fn, monad) => monad.chain(fn));

In fact, we could do the same by first applying the function that returns a functor, which gives us a nested one, and then removing the inner or the outer.

For example:

const Identity = (x) => ({
  // ...
  chain: (fn) => Identity(x).map(fn).value,
  value: x,
});

You can see that we first wrap x, then map, then grab the inner value.

Because wrapping x in a new Identity and eventually picking its inner value are opposite, it's cleaner to do none of those like in the first version.

Now let's refactor the fist snippet of this section (with nested functors) using the chain helper:

// BEFORE
// ...

// displayUserPurchases :: Object -> IO _
const displayUserPurchases = pipe(
  getUser,
  map(getLastPurchases),
  map(map(display))
);

displayUserPurchases({ email: "johndoe@whatever.com", password: "1234" });
// IO(IO(IO _))

// AFTER
// ...

const displayUserPurchases = pipe(
  getUser,
  chain(getLastPurchases),
  chain(display)
);

displayUserPurchases({ email: "johndoe@whatever.com", password: "1234" });
// IO _

First, getUser returns an IO(User).

Then, we chain getLastPurchases instead of mapping it.

In other words, we keep the result of getLastPurchases(User) (which is IO(?)), getting rid of the original IO that surrounded User.

That's why monads are often compared to onions – flattening/chaining them is like removing an onion's layer. When you do it, you're releasing potential unwanted results which could make you cry ?.

In the last example, if the first computation getUser had returned Nothing, calling chain on it would have returned Nothing too.

This functor does no operation.

However, we need to extend the simple version we saw earlier in this post in order to give it the Applicative and Monad interfaces.

Otherwise, we couldn't use it as such:

const Nothing = () => ({
  inspect: () => `Nothing()`,
  map: Nothing,
  ap: Nothing,
  chain: Nothing,
});

Nothing.of = () => Nothing();

As long as you keep at least one layer (that is one functor) until you're ready to release the effect, that's ok.

But if you flatten the monad to get the raw value contained within all over the place because you're not able to figure out how to compose it, that defeats the purpose.

Recap

Functors apply a function to a wrapped value (map).

Pointed functors have a method to place a value in the default minimum context of the functor (of).

Applicatives apply a wrapped function to a wrapped value (ap + of).

Monads apply a function that returns a wrapped value to a wrapped value (chain + of).

Exercises (Set 5)

Consider this object:

const restaurant = {
  name: "The Creamery",
  address: {
    city: "Los Angeles",
    street: {
      name: "Melrose Avenue",
    },
  },
  rating: 8,
};

Create a function getStreetName that, like the name suggests, returns the street name of the restaurant.

Use safeProp (and chain, along with any other functional helpers you need) to do so in a pure way.

// safeProp :: String -> Object -> Maybe a
const safeProp = curry((prop, obj) =>
  obj[prop] === undefined || obj[prop] === null
    ? Maybe.Nothing()
    : Maybe.Just(obj[prop])
);

// getStreetName :: Object -> Maybe String
const getStreetName = ...

Check answers.

Exercise Answers

The answers I propose are not the only ones. You may come up with your own, even better solutions.

As long as your solution works, that's great.

Set 1

Go back to exercise.

Pure functions: a, d, e / Impure functions: b, c

For e, the answer might not be easy to understand.

It was this function:

const counter = (start, end) => {
  // ...

  // e
  () => counter(start + 1, end);
};

So it's one function inside another.

We said that a pure function shouldn't rely on the outside, but here it accesses variables outside its scope, those on which it has a closure over (counter, start and end).

In a pure functional language, unlike JavaScript, counter, start and end would be immutable so e would be pure because, for the same input (in this case none), we would always get the same output.

However, values in JavaScript are mutable by default.

So if start was an object for whatever reason, it could be mutated outside of counter or inside e itself.

In this case, e would be considered impure.

But because that's not the case here, I class it as a pure function.

See this thread for more details.

const people = [
  { firstname: "Bill", lastname: "Harold", age: 54 },
  { firstname: "Ana", lastname: "Atkins", age: 42 },
  { firstname: "John", lastname: "Doe", age: 57 },
  { firstname: "Davy", lastname: "Johnson", age: 34 },
];

const uppercaseNames = (person) => ({
  firstname: person.firstname.toUpperCase(),
  lastname: person.lastname.toUpperCase(),
  age: person.age,
});

// "sort" mutates the original array it's applied on.
// So I make a copy before ([...people]) to not mutate the original argument.
const sortByAge = (people) =>
  [...people].sort((person1, person2) => person1.age - person2.age);

const parsePeople = (people) => sortByAge(people.map(uppercaseNames));

// NOT SURE TO INCLUDE
// If you have already read the section on Composition (after this one), you may come up with
// a more readable version for "parsePeople":
const parsePeople = pipe(map(uppercaseNames), sortByAge);
// or
const parsePeople = compose(sortByAge, map(uppercaseNames));

parsePeople(people);
// [
//   {firstname: "DAVY", lastname: "JOHNSON", age: 34},
//   {firstname: "ANA", lastname: "ATKINS", age: 42},
//   {firstname: "BILL", lastname: "HAROLD", age: 54},
//   {firstname: "JOHN", lastname: "DOE", age: 57},
// ]

That's the version I came with, but any variation works from the moment it has no side-effects.

The function in the exercise indeed mutates the object passed as argument.

But you can verify that the original people array is unchanged in this correction.

Set 2

Go back to exercise.

const input =
  "Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod tempor incididunt ut labore et dolore magna aliqua. Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris nisi ut aliquip ex ea commodo consequat. Duis aute irure dolor in reprehenderit in voluptate velit esse cillum dolore eu fugiat nulla pariatur. Excepteur sint occaecat cupidatat non proident, sunt in culpa qui officia deserunt mollit anim id est laborum.";

// ...

// keepLetters :: [Character] -> [Character] | []
const keepLetters = filter((char) =>
  "abcdefghijklmnopqrstuvwxyz".includes(char)
);

// getLetters :: String -> [Character]
const getLetters = pipe(
  lowercase,
  getChars,
  keepLetters,
  removeDuplicates,
  sort
);
// or
const getLetters = compose(
  sort,
  removeDuplicates,
  keepLetters,
  getChars,
  lowercase
);

getLetters(input);
// ["a", "b", "c", "d", "e", "f", "g", "h", "i", "l", "m", "n", "o", "p", "q", "r", "s", "t", "u", "v", "x"]

// getMedianAges :: [Key, [Person]] ->  [Key, Object]
const getMedianAges = reduceOverVal((acc, person) => {
  const key = `medianAge${person.sex}`;

  return !acc[key]
    ? { ...acc, [key]: person.age }
    : { ...acc, [key]: mean(acc[key], person.age) };
}, {});

// groupsMedianAges :: Object -> Object
const groupsMedianAges = pipe(getEntries, map(getMedianAges), fromEntries);
// or
const groupsMedianAges = compose(fromEntries, map(getMedianAges), getEntries);

// reduce :: (b -> a -> b) -> b -> [a] -> b

// curry :: ((a, b, ...) -> c) -> a -> b ->  ... -> c

Set 3

Go back to exercise.

const uppercaseF = map((str) => str.toUpperCase())

// Example:
const myFunctor = Just("string")

uppercaseF(myFunctor)
// Just("STRING")

const uppercaseF = map((str) => str.toUpperCase());

// Example:
const myFunctor = Just("string");

uppercaseF(myFunctor);
// Just("STRING")
```

2.

```js
// printUsername :: User -> _
const printUsername = pipe(
  safeProp("name"),
  uppercaseF,
  maybe("Username not found !", console.log)
);

// Example:
printUsername({
  name: "Yann Salmon",
  age: 18,
  interests: ["Programming", "Sport", "Reading", "Math"],
  // ...
});
// console: YANN SALMON

Set 4

Go back to exercise.

// getPartnerName :: User -> Maybe String
const getPartnerName = pipe(safeProp("partner"), map(getName));

// userName :: Maybe String
const userName = Maybe.of(getName(user));
// partnerName :: Maybe String
const partnerName = getPartnerName(user);

// couple :: Maybe String
const couple = Maybe.of(getCouplePresentation).ap(userName).ap(partnerName);
// Just("John Doe and Theresa Doe are partners.")

// ...

const couple = liftA2(getCouplePresentation, userName, partnerName);

Set 5

Go back to exercise.

// ...

// getStreetName :: Object -> Maybe String
const getStreetName = pipe(
  safeProp("address"),
  chain(safeProp("street")),
  chain(safeProp("name"))
);

getStreetName(restaurant);
// Just("Melrose Avenue")

Going further

This post is mainly inspired by what I learned from these 3 amazing resources (in order of difficulty):

Fun Fun Function playlist (video)
Functional-Light JavaScript (book)
Mostly adequate guide for Functional Programming (book)

Like me, you'll certainly find some concepts really hard to grasp at first.

But please keep going. Don't hesitate to rewind videos and reread paragraphs after a good night of sleep.

I ensure you that it will pay off.

There's also a great Github repository that gather resources about Functional Programming in JavaScript.

You'll find, among other things, nice libraries that provide functional helpers. My favorite at the time is Ramda JS. Others also provide monads like Sanctuary.

I certainly don't know everything about Functional Programming, so there are topics I didn't cover.

Those I'm aware of are:

A technique called transducing. In short, it's a way of composing map, filter and reduce operations together. Check this and that to learn more.
Other common types of monads: Either, Map, List
Other algebraic structures like semi-groups and monoids
Functional Reactive Programming

Conclusion

That's it!

Before we finish, I want to warn you about potential mistakes.

I'm not an expert in Functional Programming, so please be critical of this article as you learn more about it. I'm always open to discussions and refinements.

In any case, I hope that I laid down what I consider to be the fundamentals necessary for you to be more productive in your day-to-day work, as well as giving you the tools and the interest to go further.

And with that, keep coding! ?